Sample
Methodology Writeup for a Controlled Experiment
[rev.
Research question
Does jeering increase the proportion of eggs that fail Dr. Morse’s annual Egg Drop Competition?
Hypothesis
We predict that no statistically significant difference exists.
Outline
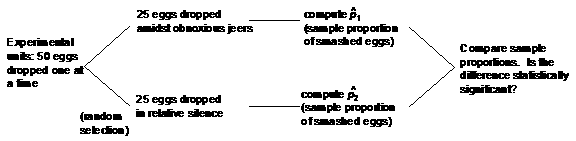
Control
Jeering script will be standardized, w/ 10 people
shouting each time. Shouting must be loud relative to background noise (which
cannot be controlled). Leader of shouting group will initiate shouting based on
coded placard in window of Rm. R: word whose 3rd letter is a vowel=shout, any
other word=silence. Placard controller will work from a secret SRS list, so
that nobody in shouting group knows in advance whether to shout or not, and
only the leader and the placard controller know the agreed-upon code. Dr. Morse
will record all data (smashed/survived) in sequence for placard controller to
copy later. Shouters will not communicate to the placard controller & will
stand out of sight of the drop zone & out of conversational earshot of
other spectators. Though shouters will surely deduce the fate of many of the
eggs, they will not record whether their efforts to trigger an egg-smash were
successful.
Shouters and Dr. Morse will make reasonable efforts to guarantee that the
experimental and control groups are independent since that is a required
assumption for the 2-proportion z test.*
Blinding (subcat. of control)
...of exp. units (eggs): not feasible.
...of researchers (placard controller & jeering crowd): partially
implemented as descr. above but cannot be fully implemented w/o damaging
realism. (If shouters are completely isolated, they will not shout w/ reqd.
emotional energy. If they are replaced w/ an amplified tape recording, the
exper. is not realistic at all.)
...of Dr. Morse: neither feasible nor desirable.
...of other bystanders: partially implemented as descr. above, but cannot be
fully implemented w/o running a separate mock egg-drop.
Randomization
Eggs are randomly assigned to “treatment” (shouting) or “control” (relative silence) before the first egg is loaded onto the release mechanism.**
Replication
Use 50 experimental units so that if we see a much larger proportion of “jeered-at” eggs getting smashed, we know the difference is too great to be plausibly caused by chance alone.***
Notes
For this experiment, a cracked egg will count as a failure.
* In truth, the independence assumption cannot be
satisfied here. We would need a very large population of eggs to draw from
(otherwise, the sampling without replacement degrades the independence of the
two groups), and we would need to know, e.g., that a run of several jeers in a
row has no effect on the next silent drop. But this is circular reasoning!
(Look at the research question again.) Can you think of a way to improve the
design?
** Another approach would be to let the leader of the jeering crowd flip a coin
each time to make the treatment/no-treatment decision (heads=jeering,
tails=silence). Doing this would also simplify the design by eliminating the
need for the placard controller. However, there are some disadvantages:
(1) There is no guarantee of getting a 25/25 split
between treatment eggs and control eggs. An equal split is desirable, as we
shall see in the 2nd semester, for simplifying the math slightly and improving
the power of the test.
(2) Coin flipping is a spectacle that invites interference from bystanders.
Even a random digit table or a calculator pseudorandom number generator would
lead to distracting questions: What are you doing? Why are you consulting that
list? What’s this all about? Can we scream with you?
(3) The best way to eliminate the communication problem among members of the
jeering group is for the leader to initiate the shouting each time. However, if
he visibly consults a list or flips a coin, it will be impossible to prevent
other members from clustering around him and wanting to know in advance what
they are to do. Egg Drop Day is characterized by moments of intense excitement
separated by periods of boredom, and it is human nature to find ways of
relieving the boredom between drops.
*** We will learn later (2nd semester) how to
calculate how many eggs are needed to detect a real experimental effect. It is
possible to show (by guess-and-check and pushing calculator buttons STAT TEST
6) that as long as the measured failure rate of “jeered-at” eggs exceeds that
of the control eggs by at least 24 percentage points (i.e., 6 or more
additional smashed eggs out of 25), then having 25 eggs in each group will always
cause the 2-proportion z test to report statistical significance.
However, this is not the way we measure the power of the test in
statistics. To measure power, which we will study in the 2nd semester, we
compute the probability that the test will report a statistically significant
difference based on assumptions about the parameter values (i.e., the
true failure rates of eggs, not the measured rates). With some number-crunching
on a spreadsheet, it is possible to show that if there are 25 eggs in each
group, if the true difference between experimental and control failure rates is
at least 20 percentage points, and if the true (parameter) failure rate for the
control group is less than .25, then the power of the test (i.e., the probability
of detecting statistical significance) is always more than 50%.
If you’re thinking to yourself, “Mr. Hansen! That’s not a very powerful test,”
guess what? You’re right. To make a more powerful test, we need to reduce the
standard deviation of the statistic involved (i.e., the measured difference between the failure proportions), and the
easiest way of doing that is to increase the sample size. With 200 eggs in
each group, and under the assumption that the true (parameter) value of
experimental minus control failure rate is at least 10 percentage points, the
power of the test exceeds 60% for all possible values of the failure
rates.
Although increasing the sample size is probably the most obvious way of increasing the power of this experiment, there
are other methods. Can you think of any?
Throughout this discussion, I have assumed that statistical significance is
defined using the traditional criterion, p < .05. We will learn what
this means in the 2nd semester. Basically, this means that chance alone would
produce a result at least this extreme less than 5% of the time.