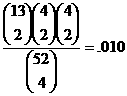|
AP Statistics / Mr. Hansen |
Name: _________________________ |
Key to
Practice Test from December 1998
Note: In most cases, work is omitted here. For full credit on your HW assignment, you must show work and circle your answers.
|
1.(a) |
P(B) = P(B | A) |
|
|
(b) |
P(A Ç
B) = P(A) P(B) |
|
|
(c) |
The middle choice is the best of the three. |
|
|
(d) |
Proof that (a) Þ (b): |
|
|
|
Statement |
Reason |
|
1. P(B) = P(B | A) |
1. Given (provided that (a) is true) |
|
|
2. P(B | A) = P(B Ç A) / P(A) |
2. Conditional prob. formula |
|
|
3. P(B) = P(B Ç A) / P(A) |
3. Transitive prop. (steps 1, 2) |
|
|
4. P(A) P(B) = P(B Ç A) |
4. Mult. prop. (mult. both sides by P(A)) |
|
|
5. P(B Ç A) = P(A Ç B) |
5. Intersection is commutative |
|
|
6. P(A Ç B) = P(A) P(B) |
6. Transitive prop. (steps 5, 4) |
|
|
Q.E.D. |
|
|
|
(e) |
Proof that (b) Þ (a): |
|
|
|
Statement |
Reason |
|
1. P(A Ç B) = P(A) P(B) |
1. Given (provided that (b) is true) |
|
|
2. P(B Ç A) = P(B) P(A) |
2. By subst., since both intersection and mult. are commutative |
|
|
3. P(A) ¹ 0 |
3. Given in (c) if you answered correctly |
|
|
4. P(B Ç A) / P(A) = P(B) |
4. Div. prop. (divide eqn. 2 by P(A)) |
|
|
5. P(B | A) = P(B Ç A) / P(A) |
5. Conditional prob. formula |
|
|
6. P(B | A) = P(B) |
6. Transitive prop. (steps, 5, 4) |
|
|
Q.E.D. |
|
|
|
(d) |
Short version: Assume (a) is true, i.e., that P(B) = P(B | A). Then P(B) = P(B Ç A) / P(A). Mult. both sides by P(A) to get (b). Q.E.D. |
|
|
(e) |
Short version: Assume (b) is true, i.e., that P(A Ç B) = P(A) P(B). If P(A) ¹ 0 [and P(A) certainly would be nonzero in order for cond. prob. involving A to have any meaning], then we can div. both sides by P(A) to get P(A Ç B) / P(A) = P(B). LHS equals P(B | A), so we have (a). Q.E.D. |
|
|
2. |
E |
|
|
3.(a) |
.9740 = .296 |
|
|
(b) |
1 – .9740 = .704, or you could say P(X ³ 1)
= .704 where X follows B(40, .03) |
|
|
(c) |
.03 since trials are independent |
|
|
4.(a) |
Denominator is 52C4
since 4 cards are dealt from a 52-card deck. (This is not poker. Although poker
questions, even simplified poker question like this one, should not appear on
the AP, you are expected to be able to perform analysis to the depth shown
here.) |
|
|
(b) |
1/(52C4) =
.00000369 |
|
|
(c) |
0/(52C4) = 0 |
|
|
(d) |
Method 1 |
|
|
5. |
There were two versions of this question to discourage cheating during the
test. Some students had a prize of $5000, others a prize of $6000. |
|
|
6. |
Assume P(A) = .15, P(B) = .01. However, on a rainy day, umbrella usage is much more common, perhaps giving P(B | A) = .25. Since P(B) ¹ P(B | A), the events are not indep. |
|
|
7.(a) |
26 · 26 · 26 · 26 · 10 · 10 · 10 = 456,976,000 |
|
|
(b) |
Yes, since there are fewer than 300 million residents. Although there are more
registered vehicles nationwide than there are licensed drivers, not everyone
has a driver’s license. |
|
|
(c) |
Some arrangements of 4 letters would not be acceptable. For example, SHED might cause some people to become distracted from the task of driving. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Answers to 7(b) challenge questions: |
|