|
Part I
|
|
|
1.(a)
|
If s is finite,
then the sampling distribution of 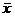 approaches N(m, s/Ön) as n ® ¥. approaches N(m, s/Ön) as n ® ¥.
|
|
|
|
|
(b)
|
Must have SRS
from pop. of interest, and s must be known. [This second requirement
is unrealistic, but until we learn about t procedures in the next
chapter, we have nothing better to use.] Rules of thumb [see p.606]:
n < 15: If data appear non-normal, do not proceed [CLT has not “kicked
in” yet].
n between 15 and 40: z procedures are valid unless we have
outliers or strong skewness.
n ³ 40: z procedures are generally valid even if pop. is highly
skewed.
|
|
|
|
|
2.(a)
|
A lot is rejected
(based on the evidence of the sample) even though the lot’s true mean kibble
mass is 1200 mg.
|
|
|
|
|
(b)
|
.05
|
|
|
|
|
(c)
|
A lot is not
rejected (based on the evidence of the sample) even though the lot’s true
mean kibble mass is not 1200 mg.
|
|
|
|
|
(d)
|
I cannot answer the
question you posed. You must tell me a specific value of the
alternative kibble mass that you have in mind.
|
|
|
|
|
(e)
|
Each alternative mean
kibble mass (say, m = 1220) has a range of possible 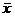 values associated
with it. (Reminder: values associated
with it. (Reminder: 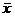 is a statistic that
is easy to compute, namely the sample mean.) We call these possible outcomes for is a statistic that
is easy to compute, namely the sample mean.) We call these possible outcomes for
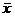 the sampling
distribution, and we draw a bell-shaped curve to indicate them. The curve
is centered on some value other than 1200. the sampling
distribution, and we draw a bell-shaped curve to indicate them. The curve
is centered on some value other than 1200.
For an illustration, see p.571 and mentally substitute 1200 for 2 and 1220
for 2.015 in the diagram. Our probability of Type II error is the amount of
the alternative sampling distribution curve that is not in the “reject”
zone(s). [For a one-sided test, there is only one “reject” zone, but in a
two-sided test, such as our dog food example, there are two “reject” zones as
shown.] In other words, P(Type II error) = the darkly shaded area.
|
|
|
|
|
(f)
|
In theory, these
curves extend infinitely far in both directions. Even if we rejected H0
only for extremely low p values (say, p < .00001 = .001%),
we would still make a Type I error .001% of the time, and we would make a
Type II error whenever the alternative sampling distribution curve is
close enough to the H0 curve to have any portion “leaking”
out of the “reject” zone(s).
|
|
|
|
|
(g)
|
No, since there
is a tradeoff between Type I and Type II error probabilities. If we simply
move the boundary [i.e., the vertical line that is immediately to the right
of the darkly shaded area on p.571] so as to reduce P(Type I error),
we will increase P(Type II error).
In the diagram on p.571, you can see a fairly good chunk of the H0
curve spilling into the “reject” zones, let us say 5% (2.5% for each tail). This value, 5%, equals P(Type
I error), which is the same as the a level, i.e., the p-value cutoff
for the test. To reduce this to .01 means moving the critical values outward—the
left one moves to the left, the right one moves to the right. But of course,
that means that more of the alternative sampling distribution curve
will spill out of the “reject” zone, thus increasing P(Type II error).
|
|
|
|
|
(h)
|
The surest bet is
to increase the sample size, thus reducing the spread (technically, the s.e.)
of the curves. Of course, there is no free lunch: This will increase the cost
of the sampling procedure somewhat.
If the left curve on p.571 becomes more sharply pointed, then the critical
value boundaries can both move inward—the left one moves right, the
right one moves left—since the central 95%, or 99%, or whatever, of the
distribution can now be contained in a narrower interval. While this does not
reduce P(Type I error), since the a level is the same as before, there is
clearly a reduction in P(Type II error). Remember, we saw in part (g)
how outward movement of the critical values caused an increase in P(Type
II error).
Or, we could leave the critical value boundaries where they are, and the new,
more sharply pointed curves would have less of the H0 curve
spilling into the “reject” zone (translation: less chance of Type I error),
and less of any alternative curve spilling out of the “reject” zone
(translation: less chance of Type II error).
|
|
|
|
|
Part II
3.
|
[Next week, we
will learn the full VHA(S)TPC
procedures for writing up a test of this type. For now, you can simply punch
buttons on your calculator (STAT TESTS 1). This is a two-sided test against m0 = 1200.]
Conclusion: Since the p-value of the test is .061 by calc., we would
not reject the lot. In other words, our evidence is not strong enough to
convince us that the lot is defective. The small difference between 1215 mg
and 1200 mg could plausibly be caused by chance alone. [Even if the lot’s
true mean is 1200, chance alone would give us a deviation this extreme or
more extreme about 6% of the time.]
|
|
|
|
|
4.
|
[We should really
use t procedures, not z procedures, on a sample this small.
However, since we haven’t learned about t yet, and since we were (unrealistically) handed the value of the population s.d. on a silver platter, we can press ahead (STAT TESTS
1) with a z test. This time, we have a one-sided test against m0 = 2000.]
Necessary step: Since n is less than 15, we must check normality. Fortunately, a normal quantile plot [show sketch] reveals no evidence of non-normality.
Conclusion: There is insufficient evidence (z = –.667, n = 8, p
= .252) to support the claim that the balance’s mean reading is less than
2000 g. A sample mean as low as or lower than the one we obtained (namely,
1997.875) could plausibly occur by chance alone, in fact more than 1/4 of the
time, even if the balance is unbiased.
|
|
|
|
|
5.
|
We can use
confidence intervals instead of tests [in fact, your book strongly recommends
doing this], but the parallels are best for two-sided tests. It is awkward to
use a confidence-interval approach in question #4 because of the one-sided
test used there.
[An example of a two-sided test accomplished through confidence intervals
would be to revisit problem #3 (punch buttons STAT TESTS 7). Since the 95%
C.I. goes from 1199.3 mg to 1230.7 mg, the value 1200 is certainly in the
central 95% of where we think the true mean lies. Thus we have insufficient
evidence to reject H0 at the 5% level of significance.
|
|
|
|
|
6.
|
[We will also do
this as a button-pusher: STAT TESTS 7. For the 3/6/2003 test, you are not required to show all
the details, but you are required to state the conclusion using the
approved wording. You may be required to show work in the calculation of
m.o.e.]
Conclusion: We are 95% confident that the true mean reading for the reference
mass is between 1991.6 g and 2004.1 g.
OR
Conclusion: We are 95% confident that the true mean reading for the reference
mass is 1997.875 ± 6.237 g.
|