Geometry / Mr. Hansen 2/5/2003

Name: _________________________ Test #7

Test on Chapter 8, plus §§9.1-9.4

	Part I: Enhanced Always, Sometimes, Never (3 pts. each). Write the letter A, S, or N in each blank. Work is not required, but if you provide a worthy diagram or a short explanation, you can earn partial credit even if your answer is incorrect. Take your time! This section has historically been where most students lose most of their points.
1. ___	Two isosceles right triangles are similar.
2. ___	Two similar figures that have the same perimeter are congruent.
3. ___	Two similar figures whose sides are in a 1:3 ratio will have areas that are also in a 1:3 ratio.
4. ___	If 17x = 44y, then the ratio x:y equals 44:17 or 44/17.
5. ___	Let i, j, k denote the lengths of the sides of one right triangle, and let l, m, n denote the lengths of the sides of another right triangle, where i/m = j/n. Then the triangles are similar.
6. ___	Two equilateral hexagons are similar.
7. ___	Two equiangular quadrilaterals are similar.
8. ___	Let two isosceles triangles be such that at least one angle of one is congruent to at least one angle of the other. Then the triangles are similar.
9. ___	Let two isosceles triangles be such that the vertex angle of one is congruent to the vertex angle of the other. Then the triangles are similar.
10.___	A triangle having sides of 3 cm, 4 cm, and 5 cm is similar to a triangle having sides of 12 miles, 15 miles, and 9 miles.
	Part II: Short Answer (4 pts. each). Complete sentences are not required, and in some cases a mere word or two (well chosen) will suffice.
11.	Define the word “proportion” as we have been construing its meaning in class. If you give an example, please note that an example without a definition will earn only partial credit.
12.	Why does Mr. Hansen require your homework solutions to include a statement of the problem, even on short ones like Ö12 where you could probably just think of the answer (2Ö3) and write it down? The reason was given in class.
13.	Given: DZWP ~ DPWN. Is segment PW an altitude to segment ZN? _____ How do you know? ________________
	Part III: Problems (6 pts. each). NO CREDIT WITHOUT WORK. Circle your answer. Unless otherwise specified, give answer in simple radical form. Include units if appropriate. Initial here if you understand these conditions: ___
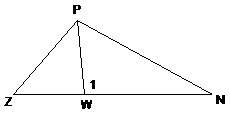
14.	In #13 without knowing the similarity condition, assume mÐ1 = 90, PW = 3, PZ = 3Ö7, ZW = 2Ö2, and WN = 8Ö2. Show that DZPN is a right triangle (showing computations), and name the theorem you use for your conclusion.
15.	Classify as acute, obtuse, right, or impossible. If it is impractical to show your work, give a reason for your answer.
(a)	A triangle having sides of length 4, 7, and 10.
(b)	A triangle having sides of length 12, 13, and 28.
(c)	A triangle having sides of length 3,000,000,000, 4,000,000,000, and 5,000,000,000.000001.
16.	The Washington Monument is 555 ft. tall. An overpriced souvenir scale model is manufactured at 1:240 scale. How tall is the model, to the nearest quarter inch?
17.	If the perimeter of a rhombus is 8Ö93 and one diagonal has a length of 16Ö3, find the length of the other diagonal.
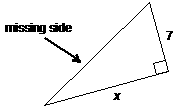
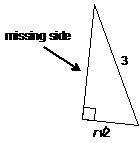
18.	Copy each diagram that is on the board and write an expression for the missing side.
(a)
(b)
19.(a)	Find the positive geometric mean between 8 and 64.
(b)	Draw a diagram that illustrates the situation in part (a) geometrically.
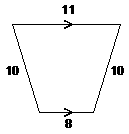
20.	Compute the height of the isosceles trapezoid shown.
	Part IV. Proof (16 points).
21.	Draw a diagram, write the “givens” and “prove,” and then furnish either a 2-column proof or a paragraph proof of the following: An isosceles right triangle inscribed in a circle (i.e., with vertices on the rim of the circle) divides the circle into arcs of 90°, 90°, and 180°.