Geometry / Mr. Hansen 5/19/2003

Name: _________________________ Test #13

Test on Chapter 14 (§14.1–§14.3 only) and Chapter 15

	Part I: Enhanced Always, Sometimes, Never (3 pts. each). Write the letter A, S, or N in each blank. Work is not required, but if you provide a worthy diagram or a short explanation, you can earn partial credit even if your answer is incorrect.
1. ___	The locus of points in a plane that satisfy a property is empty.
2. ___	The locus of points in a plane that are equidistant from the sides of a given triangle is the point at which the three angle bisectors intersect.
3. ___	The centroid of a triangle is the same point as the orthocenter.
4. ___	If a is a nonzero real number and –2a < 15, then a < –7.5.
5. ___	If DABC has mÐABC = 90, if M is the midpoint of the hypotenuse, and AB > BC, then mÐAMB > mÐCMB.
6. ___	If DABC has mÐABC = 90, if M is the midpoint of the hypotenuse, and AB > BC, then mÐC > mÐA.
	Part II: Construction (12 pts.)
7.	Use compass and straightedge to accomplish each of the following. Show your tick marks. If you have forgotten your compass, use thumb and fingernail to make a “fake compass.”
(a)	Connect points A and B with a straight line, and construct the foot F of the perpendicular from T to line AB.
	· T
	A ·                                                                             · B
(b)	Construct the bisector of ÐTFB.

	Part III: Problems (10 pts. each). Although many of these can be solved by inspection, you must make at least a rough sketch in each case to earn full credit. Circle your answer. When a numeric answer is requested, give answer either in simple radical form or with at least 3 decimal places of accuracy. Include units if appropriate. Show your work legibly and completely. If you run out of time, describe how you would solve the problem if you had more time. Initial here if you understand these conditions: ___ (2 pts.)
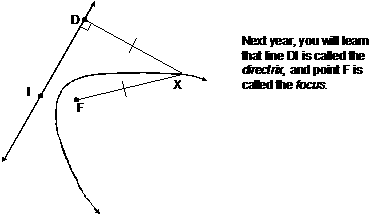
8.	Next year, in Algebra II, you will use coordinate geometry to prove that the locus of points in a plane that are equidistant from a given line and a given point not on that line is a curve called a parabola. Do not prove that today, but sketch 6 or more distance segments (i.e., 3 or more pairs) to show that the parabola on the board is a reasonable curve satisfying the given condition for point F and line DI. One pair (DX = XF) has already been done for you as an example. Just add 3 more pairs—no proof needed. [On the test as administered on 5/19/2003, you were also required to copy the diagram from the board.]
9.	Sketch and name all possible cases for the locus of points in a plane that are 5 units away from a given line l and equidistant from a given line m and a given point not on m. (Hint: The second locus is a parabola. Use that fact even if you could not answer question 8 successfully.)

10.	In DABC, AB > BC > CA. Make a sketch and indicate which angles are smallest and largest.
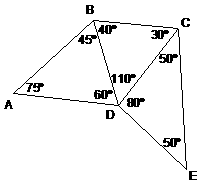
11.	Determine the shortest segment. The diagram is not drawn to scale. [On the test as administered on 5/19/2003, you were also required to copy the diagram from the board.]
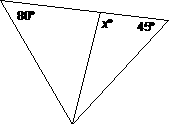
12.	State the restrictions on x. [On the test as administered on 5/19/2003, you were also required to copy the diagram from the board.]
	Part IV: Proof (15 pts.)
13.	Use the Hinge Theorem to prove that in an isosceles right triangle, a line from the right angle to the hypotenuse that is not an angle bisector must intersect the hypotenuse at a point that is not the midpoint of the hypotenuse. Make a diagram, state “Givens” and “Prove,” and write a two-column or paragraph proof. There are many, many ways to prove this, but using the Hinge Theorem is required for full credit today. Use reverse side of paper if necessary.