Solutions to Test on Chapters 14 and 15 (First 3 Sections of Each)

Geometry / Mr. Hansen
5/19/2003

Name: ___________KEY___________
Test #13

Test on Chapter 14 (§14.1–§14.3 only) and Chapter 15

	Part I: Enhanced Always, Sometimes, Never (3 pts. each). Write the letter A, S, or N in each blank. Work is not required, but if you provide a worthy diagram or a short explanation, you can earn partial credit even if your answer is incorrect.

1. _S_	The locus of points in a plane that satisfy a property is empty.
	Example: Consider the locus of points in space that have negative distance from a given point. The locus is Æ. Counterexample: The locus of points in space that are collinear with two given points is clearly nonempty.

2. _A_	The locus of points in a plane that are equidistant from the sides of a given triangle is the point at which the three angle bisectors intersect.
	Reason: ABIC. (Since radii of inscribed circle are ^ to sides of D at the points of tangency, incenter is equidistant from all 3 sides.)

3. _S_	The centroid of a triangle is the same point as the orthocenter.
	Example: In an equilateral D, circumcenter/incenter/orthocenter/centroid are all the same point. Counterexample: With most Ds, centroid and orthocenter are 2 distinct points. In fact, for an obtuse D, one is inside and one is outside the D.

4. _N_	If a is a nonzero real number and –2a < 15, then a < –7.5.
	Never true: Remember, the sign of the inequality flips if we multiply or divide by a negative number.


5. _A_	If DABC has mÐABC = 90, if M is the midpoint of the hypotenuse, and AB > BC, then mÐAMB > mÐCMB.
	Reason: AM = MC and MB = MB, so apply Converse Hinge Thm.


6. _A_	If DABC has mÐABC = 90, if M is the midpoint of the hypotenuse, and AB > BC, then mÐC > mÐA.
	Reason: Larger Ð opp. longer side.


	Part II: Construction (12 pts.)

7.	Use compass and straightedge to accomplish each of the following. Show your tick marks. If you have forgotten your compass, use thumb and fingernail to make a “fake compass.”

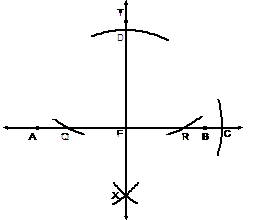
(a)	Connect points A and B with a straight line, and construct the foot F of the perpendicular from T to line AB.

	First, make arcs (both with same radius) from T to find suitable arc-centers Q and R. (Most students mistakenly assumed they could use A and B as centers. However, since it was not given that AT = BT, you must find Q and R.) Second, make two more arcs (both with same radius, though not required to be the same as QT and RT) below the line as shown, using Q and R as centers. Call point X the intersection of the arcs. Third, use straightedge to draw segment QX, constructing F at the intersection of segments QX and AB. Question: Is it acceptable to construct X above the line? Answer: Yes, but your percentage error will be reduced if you make X below the line. The closer X is to T, the more you will amplify any small errors in using the straightedge from T to X, and the more error there will be in the location of F.

	Step 1: Locate suitable points Q and R.		Steps 2-3: Using Q and R as arc-centers, find X.


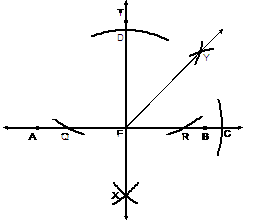
(b)	Construct the bisector of ÐTFB.

	Once again, most students made an error by using B and T as arc-centers. Although it may appear that FT = FB, that was not given. Thus the first step is to find points on rays FT and FB that are equidistant from F. Although the compass setting should not really matter, it is a good idea to use a large radius as shown to find points C and D, since then the percentage error will be smaller.

	Step 1: Locate suitable points C and D.		Steps 2-3: Using C and D as arc-centers, find Y.



	Part III: Problems (10 pts. each). Although many of these can be solved by inspection, you must make at least a rough sketch in each case to earn full credit. Circle your answer. When a numeric answer is requested, give answer either in simple radical form or with at least 3 decimal places of accuracy. Include units if appropriate. Show your work legibly and completely. If you run out of time, describe how you would solve the problem if you had more time. Initial here if you understand these conditions: ___ (2 pts.)

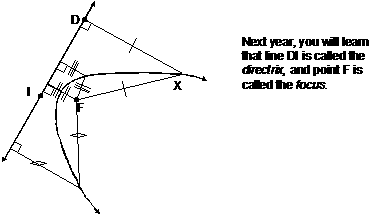
8.	Next year, in Algebra II, you will use coordinate geometry to prove that the locus of points in a plane that are equidistant from a given line and a given point not on that line is a curve called a parabola. Do not prove that today, but sketch 6 or more distance segments (i.e., 3 or more pairs) to show that the parabola on the board is a reasonable curve satisfying the given condition for point F and line DI. One pair (DX = XF) has already been done for you as an example. Just add 3 more pairs—no proof needed. [On the test as administered on 5/19/2003, you were also required to copy the diagram from the board.]

	Note that the right angle marks are required in order to show distance from a point on the parabola to the directrix.

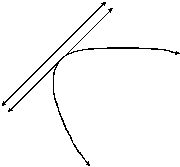
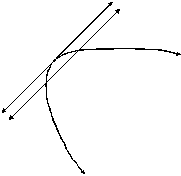
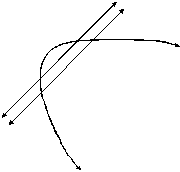
9.	Sketch and name all possible cases for the locus of points in a plane that are 5 units away from a given line l and equidistant from a given line m and a given point not on m. (Hint: The second locus is a parabola. Use that fact even if you could not answer question 8 successfully.)

	Solution: The first locus is a pair of parallel lines (5 units on each side of l), and the second locus is a parabola.

	Case I: Æ (no intersection)	Case II: 1 point in the intersection		Case III: 2 points in the intersection


	Case IV: 3 points in the intersection	Case V: 4 points in the intersection


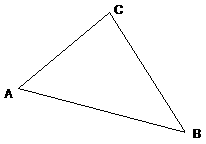
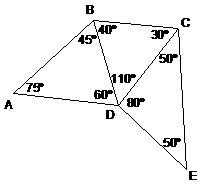
10.	In DABC, AB > BC > CA. Make a sketch and indicate which angles are smallest and largest.

	Solution: No work is required, but clearly ÐC is largest (opp. longest side), and ÐB is smallest (opp. shortest side). ÐA is somewhere in between.

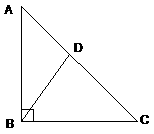
11.	Determine the shortest segment. The diagram is not drawn to scale. [On the test as administered on 5/19/2003, you were also required to copy the diagram from the board.]

	Solution: In DCDE, CE > CD = DE. In other words, segments DE and DC are tied for the title of “shortest.” But in DBCD, which has a side in common, side BD is shorter yet. And in DABD, we see that side AD is shortest of all. Answer: segment AD. This problem can be done by inspection for full credit.

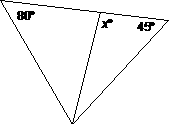
12.	State the restrictions on x. [On the test as administered on 5/19/2003, you were also required to copy the diagram from the board.]


	Answer: 80 < x < 135. Work was not required, but if you wished, you could show work as follows: Let A be the vertex with the given 80º angle, B the vertex with the 45º angle, C the remaining vertex of the large triangle, and D the unknown point lying between A and B. Since xº is an ext. Ð to DADC, x > 80. (An ext. Ð always exceeds any remote int. Ð.) However, in DDBC, x can never equal or exceed 135, since that would force the angles of DDBC to add up to more than 180º. Conclusion: 80 < x < 135.

	Part IV: Proof (15 pts.)

13.	Use the Hinge Theorem to prove that in an isosceles right triangle, a line from the right angle to the hypotenuse that is not an angle bisector must intersect the hypotenuse at a point that is not the midpoint of the hypotenuse. Make a diagram, state “Givens” and “Prove,” and write a two-column or paragraph proof. There are many, many ways to prove this, but using the Hinge Theorem is required for full credit today. Use reverse side of paper if necessary.

	Given: Isosceles rt. DABC w/ rt. ÐABC; ray BD does not bisect ÐABC Prove: D is not the midpoint of segment AC

	General comment: The result is true for any isosceles triangle with vertex at B, not merely an isosceles right triangle. We learned last fall that in any isosceles triangle, a line bisects the vertex angle iff it bisects the base. We also learned that both of those conditions are true iff the line is ^ to the base, i.e., iff ÐCDB is a rt. Ð. Nowhere is it required that ÐABC be a right angle. The only reason for wording the problem as it was worded was to throw you off the track slightly—you have to think for a moment to see that AB and BC are leg lengths.

	Method 1 (direct 2-column proof)
	1. Isosc. rt. DABC w/ rt. ÐABC	1. Given
	2. Segments AB, BC are legs	2. Def. of legs of isosc. rt. D
	3. AB = BC	3. Legs. of isosc. D are @
	4. DB = DB	4. Refl.
	5. ray BD does not bisect ÐABC	5. Given
	6. mÐABD ¹ mÐDBC	6. Def. bis.
	7. mÐABD > mÐDBC xor mÐABD < mÐDBC	7. Trichotomy [see p.687 of textbook]
	8. AD > DC xor AD < DC	8. Hinge Thm.
	9. AD ¹ DC	9. Trichotomy/restatement of step 10
	10. D is not mdpt. of sAC	10. Def. mdpt.
	Q.E.D.

	Method 2 (proof by contradiction)
	Assume (bwoc) that D is the mdpt. of sAC. Then AD = DC. Since ray BD does not bisect ÐABC, assume wlog [justified below] that ÐABD < ÐDBC. Since AB = BC (legs of isosc. rt. D) and DB = DB (refl.), we know by Hinge Thm. that AD < DC, a contradiction. (Q.E.D.)

	Note: The claim that ÐABD < ÐDBC wlog is legitimate, since the diagram is symmetric. After all, if someone objected strongly, we could simply interchange points A and C and continue.

	Method 3 (direct paragraph proof)
	Since the legs of an isosc. rt. D are @, AB = BC. Since ray BD does not bisect ÐABC (given), one of ÐABD or ÐDBC must be larger than the other. Wlog, assume ÐDBC is the larger. We know DB = DB (refl.), so by Hinge Thm., DC > DA. By def. of mdpt., D is not the mdpt. of sAC. (Q.E.D.)