FAQs
Q.
A.
Is this for a grade?
Yes. However, I anticipate that everyone will earn 100%. Therefore, this is probably even better than a happy quiz.
Q.
A.
May we work alone?
No. Work with a partner to help you take your readings and to double-check your work.
Q.
A.
May we submit one paper for our group?
No, each person needs to submit his own paper.
Equipment
¨
¨
¨
Yardstick with string or cord
Binder clip attached to yardstick
Protractor and plumb line (in plastic baggie)
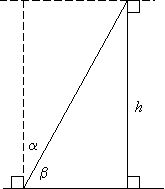
Task
1.
On diagram, mark top of tower as point T, the foot as F, and the place from which you and your partner will use your protractor as P.
2.
Remove binder clip and place in pocket for safekeeping.
3.
Slowly unwrap string, turning yardstick end to end and keeping string fairly taut to avoid tangles. (WARNING: If you remove string all at once, you will make a huge tangled mess.)
4.
Longer is better when pacing out distance PF. Reason: If
b is a large angle (close to 90°), then a small error in b can produce a _____ error when we compute _____ , which is the goal of this exercise.If you had several hundred feet of string, the easiest and most accurate way to find h would probably be to let out string until angle _____ became exactly _____ degrees, since right triangle TFP would then be ___________. In other words, h would simply equal _____ on the diagram, which would be the length of the string.
5.
However, you don’t have several hundred feet of string, and for safety’s sake you shouldn’t be using your protractor too close to Wisconsin Avenue. When string is fully unwrapped, one person should stand at foot of tower holding yardstick perpendicular to ground, with end of string at waist level. Then move the entire string (avoiding tangles!) so as to measure out 2 or 3 string lengths going away from foot of tower. Record your data here:
We used ________ string lengths.
NOTE: String length is marked in red ink on end of yardstick near "STA Math Dept." label. String length does not include yardstick’s length, so be sure to hold yardstick perpendicular to ground.
Because the string is marked as ________ feet, PF = ____________ . (Please also label length PF on diagram.)
6.
Carefully rewrap your string onto yardstick (end to end) and secure it with binder clip. Raise your hand when you have done this so that Mr. Hansen can collect your yardstick and help you if necessary.
7.
Carefully measure acute angle
a by having one person sight point T along flat edge of protractor while the other adjusts protractor arm so that plumb line hangs straight. Record your data here, as accurately as you can:a = _________
8.
Since
b is the _________________ of a, we know b = ____________ .If a brave stonemason were working at the very top of the tower (T) and looked down at you and your partner as you used the protractor, what would be the angle of depression from T to P? ______________ Is this the same as the angle of elevation from P to T? ________
(9.)
(Optional step—not required for full credit. Do this only if you are working much faster than the other groups. Take additional protractor reading(s) farther from foot of tower, recording
a and PF each time. Then, in step 10, you could average all your results for h for better accuracy.)10.
Write and solve a trigonometry equation for h. Please work with your partner to do this two different ways: One partner should make a trigonometry equation involving
a, and the other should make a trigonometry equation involving b. The a method is a bit more challenging but should still be straightforward.Show work in space below or, if you prefer, next to diagram. Give answer to nearest foot, and check to make sure that your answer matches your partner’s answer.