|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
|
d
b
c
c
d
a, c
S
S
A
A
A
N
|
|
17.
|
1. sAB ^ sAD, sDC ^ sAD
2. ÐA,
ÐD
are rt. Ðs
3. ÐA
@
ÐD
4. E is midpt. of sAD
5. sAE @ sDE
6. sAB @ sCD
7. DABE
@
DDCE
8. sBE @ sCE
9. ÐEBC
@
ÐECB
|
1. Given
2. Def. ^
3. All rt. Ðs
are @
4. Given
5. Def. midpt.
6. Given
7. SAS (5, 3, 6)
8. CPCTC
9. ITT
|
|
18.
|
1. circle O
2. sAB ^ sCD, sEF ^ sCD
3. add dotted segments sOA,
sOE
4. sOC @ sOD
5. sBC @ sFD
6. sOB @ sOF
7. ÐABO,
ÐEFO
are rt. Ðs
[optional] 8. DABO,
DEFO
are rt. Ds
9. sOA @ sOE
10. DABO
@
DEFO
11. sAB @ sEF
|
1. Given
2. Given
3. 2 pts. determine a line (or segment)
4. Radii of circle are @
5. Given
6. Subtr. prop. (4, 5)
7. Def. ^
8. Def. rt. D
9. Same as 4
10. HL (9, 6)
11. CPCTC
|
|
19.
|
1. sAD is alt. to sBC
2. sAD ^ sBC
3. ÐADB,
ÐADC
are rt. Ðs
4. ÐADB
@
ÐADC
5. sAD @ sAD
6. sAD bis.
ÐBAC
7. ÐBAD
@
ÐCAD
8. DADB
@
DADC
9. sBD @ sDC
10. D is midpt. of sBC
11. sAD is median to sBC
|
1. Given
2. Def. alt.
3. Def. ^
4. All rt. Ðs
are @
5. Refl.
6. Given
7. Def. bis.
8. ASA (4, 5, 7)
9. CPCTC
10. Def. midpt.
11. Def. median
|
|
20.
|
1. DABC
isosc. w/ sAB @ sAC
2. D midpt. of sAB, E midpt. of sAC
3. sDB @ sEC
4. ÐABC
@
ÐACB
5. sBC @ sBC
6. DDCB
@
DEBC
7. ÐDCB
@
ÐEBC
8. DPBC
is isosc.
|
1. Given
2. Given
3. Div. prop.
4. ITT (using given in step 1)
5. Refl.
6. SAS (3, 4, 5)
7. CPCTC
8. ITT (using base Ðs in step 7)
|
|
Practice 1
|
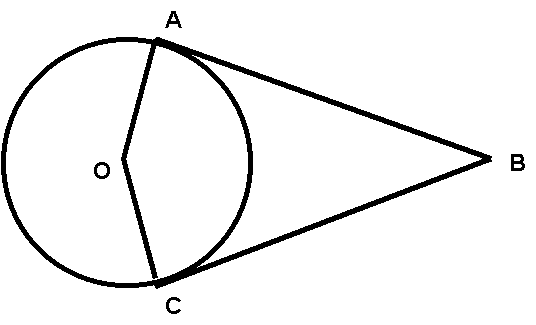
Given: circle O
sOA ^ sAB
sOC ^ sCB
Prove: sAB @
sBC
1. circle O (given)
2. sOA ^ sAB, sOC ^ sCB (given)
3. OA = OC (radii are @)
4. draw dotted segment from O to B (2 pts. determine
a line)
5. OB = OB (reflexive)
6. ÐOAB, ÐOCB are rt. Ðs (def. ^)
7. DOAB @ DOCB (HL, steps 6,
5, 3)
8. sAB @ sBC (CPCTC)
Sam Empson’s clever alternate version:
1. circle O (given)
2. sOA ^ sAB, sOC ^ sCB (given)
3. OA = OC (radii are @)
4. draw dotted segment from A to C (2 pts. determine
a line)
5. ÐOAC @ ÐOCA (base Ðs of isosc. DOAC)
6. ÐCAB compl.
ÐOAC, ÐACB
compl. ÐOCA
(def. ^, def. compl.)
7. ÐCAB @ ÐACB (compls. of @ Ðs are @)
8. sAB @ sBC (isosc. Û base Ðs @)
|
|
Practice 2 (tepee problem)
|
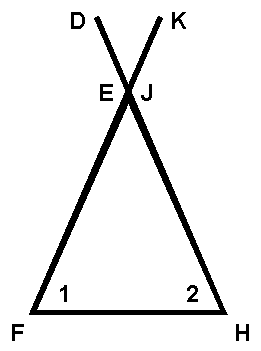
Given: Ð 1 @ Ð 2
DH = KF
Prove: DE = KJ
1. Ð1 @
Ð2 (given)
2. EF = JH (base Ðs @ Û
isosc.)
3. DH = KF (given)
4. DE = KJ (subtr. prop.)
|