Geometry / Mr. Hansen 5/16/2003

Name: _______________________

Two Proofs from §15.3 (Hinge Theorem)

	Note: These proofs should help you prepare for Monday’s test. In class on Friday, 5/16/2003, I did not cover these very well. In fact, the proof I gave for #14 in D period contained several errors: -- First, there is no need for an auxiliary segment from A to D. -- Second, the reason for step 5 (see line marked * below) is not Converse Hinge Thm. but the simpler result from §15.2. In fact, we have been using this principle since early last fall: In any triangle, the longer side is always opposite the larger angle and vice versa. -- Finally, the correct statement in step 5 is ÐC > ÐE. I think I may have written the reverse, and if so, I apologize. Please correct your notes accordingly, or if you did not take notes, please simply study the version below and ignore the original. Because of the unacceptably high number of mistakes I made in the chalkboard version of #14, I have decided to award a class typo point to everyone in both sections. The versions below should be correct and complete. If you find any additional errors or have any questions, please contact me by e-mail or voice mail. Note that #15 does not use the Hinge Theorem at all.
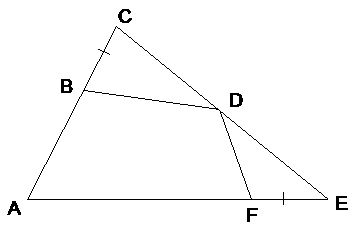
p.700, #14.
	1. AC < AE	1. Given
	2. D mdpt. of sCE	2. Given
	3. CB = FE	3. Given
	4. AE > AC [optional step]	4. Restatement of 1
*	5. ÐC > ÐE	5. Larger Ð opp. longer side [§15.2]
	6. CD = DE	6. Def. mdpt.
	7. BD > FD	7. Hinge Thm. (steps 3, 6, 5)
	Q.E.D.
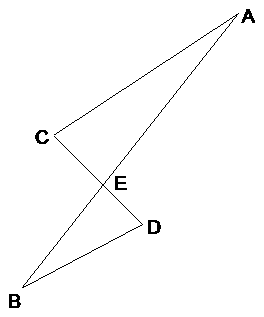
p.700, #16.
	1. ÐC > ÐA	1. Given
	2. AE > CE	2. Larger Ð opp. longer side
	3. ÐD > ÐB	3. Given
	4. EB > ED	4. Larger Ð opp. longer side
	5. AE + EB > CE + ED	5. Add. prop. [add inequalities in steps (2) and (4): “larger + larger” must exceed “smaller + smaller”]
	6. AB > CD	6. Subst. (def. of segment addition)
	Q.E.D.