|
Geometry / Mr. Hansen |
Name: _________________________ |
Example
of a “Diagramless” Proof
Where You Have to Create Your Own Diagram, “Givens,” and “Prove”
|
|
Note: The example posed in class (the proposition that if there are two congruent medians in a D, the D is isosceles) is really too hard to prove right now. By the end of the year we will be able to prove this quite readily using analytic geometry, but for now, let’s try another example. |
|
|
Problem. |
Show that an altitude of an equilateral triangle is also a median of the triangle. (This is #7 on p.159.) |
|
|
Solution. |
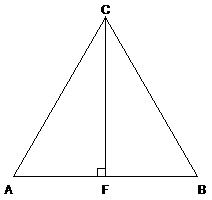
First, remember that you need to be totally general. However, use your common sense. What side is this altitude supposed to be the median of? Answer: obviously, the same side that it connects to as an altitude. When you draw the diagram of an equilateral D, notice that the side to draw the altitude to can be chosen at random since the D can be rotated wlog (i.e., without loss of generality). |
|
|
|
Second, draw a diagram and label all the points you are likely to need. Make your drawing fairly large, just in case you need to add an auxiliary (dotted) line later. |
|
|
|
|
|
|
|
Third, mentally reword the claim in the “Problem” to use “if-then”
wording. If there is an equilateral
triangle with an altitude drawn, then that segment is also a median. You
usually do not need to write this part out, unless it helps you. |
|
|
|
Fourth, write the “if” part as your “givens” and the “then” part as your “prove,” but this time using the labels in your diagram. Be concise, but be sure to cover everything! |
|
|
|
Given: DABC
is equilateral |
|
|
|
Look everything over very carefully before you begin your two-column
proof. Mark up a scratch copy of your diagram as you prepare to use some
combination of backward chaining and forward chaining to find a path that
leads to the conclusion. Ready? Go! |
|
|
Proof. |
1. DABC
is equilateral |
1. Given |