Answers to Selected Review Problems, Chapters 8 and 9

Geometry / Mr. Hansen
2/4/2003, rev. 2/22/2003

Name: _______________________

Answers to Selected Review Problems
Chapters 8 and 9

	pp. 361-363
1.	The means are b and c; the extremes are a and d.
3.	The geometric means (that’s the name we use) would be ±10. If this were a diagram where we were calculating h (altitude), we would just say 10, but as posed, the question must be answered by ±10.
4.	±3Ö2
5.	4/9
6.	DF = 9 EF = 7.5
9.	2br/(3a)
10.	20 m
12.	ST = 90/13 TV = 40/13 PT = 72/13
14.	x = 12 by ABT
15.	about 879 ft.
16.	EO = 6/5 EK = 9
18.	1. BRXZ is a parallelogram	1. Given
	2. ÐR @ ÐZ	2. Prop. parallelogram (opp. Ðs @)
	3. Ð3 @ Ð4	3. Given
	4. DRCW @ DZYA	4. AA~
	5. RC/RW = ZY/ZA	5. CSSTP
	6. (RC)(ZA) = (ZY)(RW)	6. Cross-mult.
	Q.E.D.
19.	(–13, 0) by ABT
20.(a)	A
(b)	A
(b.5)	If we are given only that an angle of one isosceles triangle is congruent to an angle of another isosceles triangle, are the triangles similar? Answer: The triangles may be similar as in parts (a) or (b), but it is also easy to construct a counterexample. Consider one isosceles triangle whose base angles are each 50° and another triangle whose apex angle is 50°; clearly these triangles are not similar. The answer to “b.5” is Sometimes.
(c)	N
(d)	S
(e)	N
(f)	A
(g)	A
(h)	S
25.	30 cm

	pp. 429-433
1.(a)	EG = 6 is the geometric mean between HG = 4 and GF = unknown. Therefore, 4/6 = 6/GF, from which GF = 9.
(b)	By Leg Facts, (EH)² = 4 · 16. Therefore, EH = 8.
(c)	By Leg Facts, (2Ö5)² = 4HF. Therefore, HF = 5 after you solve the equation. (Remember that when you square the 2Ö5, you must square both the 2 and the Ö5.)
(d)	This is the easiest of the group. Just use Pythag. Thm. to get HF = Ö13.
2.(a)	The clue is the hypotenuse that is twice the length of the short leg: 30°-60°-90° family.
(b)	3,4,5 family
(c)	5,12,13 family [missing side is 26]
(d)	8,15,17 family [missing side is 7.5]
(e)	45°-45°-90° family
3.(a)	30 [by inspection, using 8,15,17 Pythagorean triple]
(b)	base = 5, height = 5Ö3 The trick is to create a mirror image triangle so as to form a large equilateral triangle. Then, since we know the base is half of 10, we have 5² + h² = 10², which we solve for h to get h = 5Ö3.
(c)	7 [by inspection, using 7,24,25 Pythagorean triple]
(d)	15 [by inspection, using 3,4,5 family]
(e)	4Ö5 [same comment as for (d)]
(f)	9
(g)	5Ö3 and 10Ö3, respectively This is similar to part (b), only harder. Let the unknown leg be x. The hypotenuse must be 2x. Do you see why? Think of the trick we used in part (b). After you have figured out why the hypotenuse is 2x, you can write the equation x² + 15² = (2x)², which you can solve to get x = 5Ö3 as claimed.
(h)	12.5 [use 7,24,25 family]
(i)	26
(j)	4Ö2 for each
4.	40 [by inspection, since each hypotenuse is 10 by inspection]
5.	Draw an altitude to the base. This altitude bisects the base, creating 2 congruent 30°-60°-90° triangles with short leg of 3 and hypot. of 6. Altitude is 3Ö3 by inspection [using what we learned about 30°-60°-90° triangles].
6.	5 km [make a sketch and build a 3,4,5 right triangle]
6.(alt.)	If the person starts at the South Pole, the answer is 3 km, since “west” means traveling along the arc of a rather small circle. This would make a good brain teaser!
7.	7 ft. [by inspection, using 7,24,25 Pythagorean triple]
8.	This is reminiscent of #5. The altitude bisects the base [prop. of isosc. D], so we can examine the smaller right D having a leg of 3 and hypotenuse of 8. By Pythag. Thm., the other leg [i.e., the altitude of the original D] is Ö55 » 7.4.
9.	This is like #5, except in reverse. Since the altitude is 8Ö3, half the base must be 8 by inspection [prop. of 30°-60°-90° triangle]. The full base is therefore 16. Multiply by 3 to get perimeter = 48.
10.	Ö29 by Pythag. Thm.
11.	Ö85 [trick is to drop an auxiliary line from R that forms a right angle with the side of length 13] Many, many people missed test problem #20, which was slightly harder but of the same general type. In that problem, you had to drop 2 auxiliary altitudes to see that the same amount was being trimmed off the upper base of the trapezoid from both the left and the right. Make sure you know how to do this, since it’s a safe bet that another problem of this type will be appearing in your future.
12.	Drop an altitude from X down to segment VW, and call the point of intersection A. Then, because of the symmetry of an isosceles trapezoid, VZ = AW = 2, and TXAZ is a rectangle. Since mÐV = 30, DVTZ is a 30°-60°-90° triangle, and TZ = 2/Ö3 by inspection, which we simplify to (2Ö3)/3. TV is twice that, or (4Ö3)/3. [Because TVWX is an isosceles trapezoid, TV = XW. Since altitude TZ = XA, DTVZ @ DXWA by HL, and then VZ = AW by CPCTC. These are the details if you want a rigorous proof of why VZ = AW, which we glibly did above by appealing to “symmetry.”]
13.	By the procedure we learned in class, the long diagonal is the square root of (4² + 3² + 12²), or simply 13. [This generalizes to higher dimensions, too. For example, the distance between space-time coordinates (a, b, c, d) and (e, f, g, h) will be the square root of ((a – e)² + (b – f)² + (c – g)² + (d – h)²).]
14.	By inspection, RS = 15 [3,4,5 family], and RS equals half the length of a side of square JKMO [prop. of squares]. [Further explanation, in case you can’t see this immediately: Since line PR is the ^ bisector of segments KO and MJ, and since KO = MJ by prop. of squares, any point on line PR is equidistant from all 4 points J, K, M, and O. Therefore, point R, which is in plane OJK, must be the center of square JKMO. S is the midpoint of side JK by prop. of isosceles DPKJ, so segment RS, which connects the center to side JK, must form a 45°-45°-90° triangle, DRSK, as we have seen many times before. That means RS = SK, so each side of base JKMO must be twice that.] Since each side of square JKMO is twice RS, each side is 2(15) = 30. Perimeter is 4(30) = 120.
15.	This is like #13. The long diagonal is the square root of (length² + width² + height²). Answer: Ö209 » 14.5.
16.(a)	CB = 8 by inspection [8,15,17 family]
(b)	AD = 7.5 [by similar Ds]
(c)	AE = 8.5 [by similar Ds]
(d)	EB = 8.5 [by subtracting part (c) from 17]
(e)	DC = 7.5 [using parts (b), (c), (d), and Side Splitter]
17.	By distance formula, d = square root of ((Dx)² + (Dy)²), or the square root of (3² + 4²), or simply 5.
20.(a)	180 [technically, no degree symbol since “measure” was specified]
(b)	5p [diameter is 10 by Pythag. Thm., so circumference is 10p; final answer is half of that since arc RTC is a semicircle]
(c)	A = A_circle – A_square = pr² – wh = p(5²) – (8)(6) = 25p – 48 » 30.5
23.	After 3 hours, A is 60 km north of the harbor and B is 45 km west of the harbor. Hypotenuse is 75 km by inspection [3,4,5 family].
24.(a)	By Leg Facts, 10² = 8(8 + x), which we solve to get x = 4.5.
(b)	By Leg Facts, 6² = y(y + 9), which we solve to get y = –12 or y = 3. However, since the answer is a length, we reject the negative solution. Final answer: y = 3.
25.	If the stick figure boy swims along the hypotenuse, the distance is Ö10 » 3.162 mi. Because d = rt [distance = rate · time, which I hope you remember from algebra], the time required is d/r = 3.162 mi / 2 mph » 1.58 hr. However, if the boy swims along the 1-mile leg (which takes half an hour) and then walks to the Golden Arches (3/4 of an hour), his total travel time is only 1.25 hr. Clearly, it is better to swim straight across and then walk, even though that makes the total distance longer. If you take calculus, you will learn that better solutions are possible. In fact, the minimum time needed to reach the Golden Arches through a combination of swimming and walking is only about 1 hour and 11 minutes. How is this possible? Send me an e-mail giving the answer (for 2 bonus points) or an e-mail saying, “I don’t know, but I read the question” (for 1 bonus point). Either way, I’ll know that my time preparing this handout was well spent because students were benefiting from the solutions.
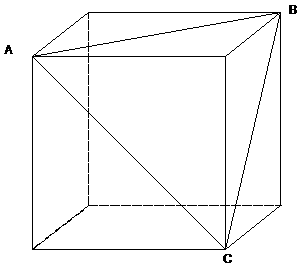
28.	Draw a picture. The digging point is 24 paces east (30 – 6) and 45 paces north (20 + 25). These legs of 24 and 45 give a hypotenuse of 51 paces [8,15,17 family]. Did you get this to work out? Please reread the solution to question 25 for a bonus point opportunity.
37.(a)	Let 1 = length of a side. [This is wlog, since we can choose any measurement units we like so that the side has length 1.] Then each face diagonal is Ö2, and the long diagonal is Ö3. Let us call these lengths f and d, respectively. If you draw them intersecting at a vertex of the cube, they form a right D with legs of 1 and f, and hypotenuse d. The angle between these two segments must be arcsin(1/d) » 35°. Note that there are other ways of getting the same answer: You could also use arcos(f/d), or you could use arctan(1/f).
(b)	This is really hard to visualize unless you are good with 3-D artwork, but since the face diagonals are meeting at a vertex, they must belong to different faces. If you connect their endpoints to form a triangle, the third side is also a face diagonal. Since all face diagonals of a cube are congruent, the triangle is equilateral. Answer: 60°. In the diagram below, segments AC and BC are face diagonals meeting to form ÐACB. Can you see why this is 60°?

	pp. 437
24.	Since face diagonals of a cube are congruent, DAHF is equilateral. [This is the same situation as in #37(b) from the previous set.] Since HE = EF = 6, we know HF 6Ö2 by our 45°-45°-90° properties. J is a midpoint, so JF = 3Ö2. Since DAJF is a 30°-60°-90° triangle, we can multiply by Ö3 to get AJ. Answer: 3Ö6.