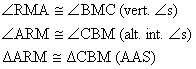Geometry / Mr. Hansen 4/9/2003 [rev. 4/19/2005, 4/10/2010]

Name: _________________________

Answer Key for Chapter 11 Review Questions
pp. 554-558

Note:

• In most cases, only the answers are shown below. On your test, you must also show clear, complete work for full credit. That generally means formula, plug-ins, and work leading to answer.
• If you have any questions, please send e-mail or voice mail. Both are available 24 hours. If I have gone to sleep, I will respond the next day.

1.	(a) 84 sq. units (b) 42 sq. units [half as much as (a)] (c) 75 sq. units (d) 52 sq. units (e) 20 sq. units (f) 8 sq. units
2.	(a) 63 sq. units (b) 33 sq. units
3.	(a) 70 sq. units [reason: BH – bh = (13)(7) – (3)(7) = 91 – 21 = 70] (b) 24 sq. units (c) 16 sq. units [Use any of the following methods, your choice: (1) standard formula with height of 4, (2) the equilateral area formula, or (3) Hero’s formula.]
4.	A = (20)(4) = 80 m^2 total cost = (unit cost)(area) = ($15/m^2)(80 m^2) = $1200
5.	48 sq. units
6.	288 sq. units
7.	18 sq. units
8.	A = Alternate method: A = Either way, total cost = (unit cost)(area) = ($.03/dm^2)(22.5 dm^2) = $0.675.
9.	196 sq. units
10.	64 sq. units
11.	81 m^2 [reason: perimeter is 36 m each side s is 9 m A = s^2 = (9 m)^2 = 81 m^2]
12.	d = 14 mm r = 7 mm Asemicircle =
13.	(a) 9 sq. units (b) 16 sq. units [reason: Aannulus = R^2 – r^2 = (5^2) – (3^2) = 25 – 9 = 16] (c) (100 – 25) sq. units
14.	(a) 24 sq. units (b) 16 sq. units (c) 4 sq. units [Note: Make sure that you can also solve for unusual central angles such as 57°30'.]
15.	(a) 5 : 8 (b) 9 : 16 [reason: corresponding sides are in ratio 18 : 24, or 3 : 4, so we square to get 9 : 16]
16.	(–2, 0)
17.	360 sq. units [by Hero’s Formula]
18.	Draw a sketch. Depending on which side you choose to call the “base,” height h is either or by properties of 45°-45°-90° s. These simplify to h = 3 or h = 3.5, using b = 7 or 6, respectively. However, regardless of which method you are using, A = bh = .
19.	120 sq. units
20.	sq. units
21.	A = sq. units perim. = 50 units
22.	By Pythag. Thm. (or distance formula, which is equivalent), r = . (a) C = 2r = 2 40.2 (b) A = r^2 = (41) 128.8 sq. units
23.	(a) each side s = [do not simplify, since we will be squaring in a moment anyway] A = s^2 = = 338 sq. units (b) A = s^2 = 18 s = [do not simplify, since we will be multiplying in a moment anyway] diagonal = s = = 6 units
24.	apothem = a = 18 by inspection By drawing 30°-60°-90° s, we see that half of any one side is . Thus each side is , and perimeter = p = . A =
25.	(a) = 40 – 6.4 = 33.6 sq. units [steps missing, but you should fill them in] (b) (27 – 9) sq. units (c) [A clever little problem!] By TTT, segments that appear to be 2 and 3 actually are 2 and 3, respectively. The 2 short segments in the lower left corner are both of length 1, since they form 2 of the 4 sides of a 1-by-1 square whose upper right corner is the center of the circle. Thus the is a 3-4-5 rt. having , and the circle clearly has area (1^2) = . Final answer: A = .
26.	(a) Ashaded = Aunshaded since same base and height, so Awhole : Ashaded = 2 : 1. (b) Let x = unmarked segment length. By ABT, Solve for x to get x = 1.2. Then Awhole = 4.2 [steps omitted] and Ashaded = 3 [steps omitted], so Awhole : Ashaded = 4.2 : 3 = 7 : 5. [It is acceptable to give answer as 4.2 : 3 if you cannot see the equivalent 7 : 5 ratio.] (c) By Midline Thm., each side of whole figure is twice as long as corresp. side in small . Therefore, ratio of areas is (2)^2 = 4 : 1.
27.	(a) (9p – 18) sq. units [same method as in §11.6 #11a] (b) (6p – 9) sq. units [same method as in §11.6 #11b]
28.	(a) 16 : 81 [reason: similar figures, so square the ratio of corresp. sides] (b) 4 : 9 [same reason as in part (a), but here the corresp. sides are 6 and 9] (c) 1 : 1 [regions are actually this time]
29.	Square is 25 by 25, or 625 sq. units. Circle has diam. of Answer: Circle has greater area.
30.	MR = MB (def. mdpt.) Therefore, ACAT = ABMAT + ACBM = ABMAT + AARM = ABRAT. (Q.E.D.)
31.	(a) (12, 13) (b) 156 sq. units
32.	(a) Since AII : Awhole = by similar figures, AI is of the whole. Therefore, AI : AII = 5 : 4. (b) Since AI : Awhole = by similar figures, AII is of the whole. Therefore, AI : AII = 100 : 156 = 25 : 39.
33.	Draw diagram with upper base of 2, lower base of x + 2 + x (with a segment of length x poking out to the left and right), and legs that must be each 2x (by properties of 30°-60°-90° s). Then perim. = x + 2 + x + 2x + 2 + 2x = 70, forcing x to be 11. [You must solve the equation.] Apply trapezoid area formula [steps omitted] to get A = .
34.	Join the triangles together so that the supplementary angles meet to form a straight angle. You then have a figure clearly showing two triangles having same base, same height. (Q.E.D.)
35.	(18 – 9) sq. units [hard]
36.	(a) (100 – 50) sq. units [hard] (b) [Another clever problem that is easy if you see the trick.] Draw an auxiliary segment from the center, upward and to the right until it meets the intersection of the chord and the circle. Now you have separated the shaded area into a 30°-30°-120° triangle and a sector. Ashaded = Atriangle + Asector = [You need to show that the rightmost central is 60°, but that is not hard to do]. After a bit of algebra, the sum above becomes 9 + =
37.	432 sq. units
39.	(72 – 24) sq. units [hard]
40.	Agrazing = (Acircle of radius 12) + (Acircle of radius 4) + (Acircle of radius 2) = (12^2) + (4^2) + (2^2) = 108 + 4 + =
41.	[Hard.] Let x denote double-tick length. By Pythag. Thm., you can prove that x = 4.5 [see steps below]. Ashaded = A“Batman” region – Acircle of radius 3 = Asemicircle of radius 9 – (3^2) = ((9^2)) – 9 = . [Note how we used §11.6 #13b as a lemma.] Explanation of why x = 4.5: Let C be the center of the radius-3 circle. Let B be the center of the large semicircle (i.e., the point directly underneath C). Let A be the center of the small semicircle on the right half of the diagram. Then ABC is a right triangle with right angle at B. Now observe that AB = large radius – 3 = 2x – 3, BC = x by inspection, and AC = x + 3 by inspection. By Pythag. Thm., (2x – 3)^2 + x^2 = (x + 3)^2. By algebra, this eventually simplifies to x = 4.5.