6.
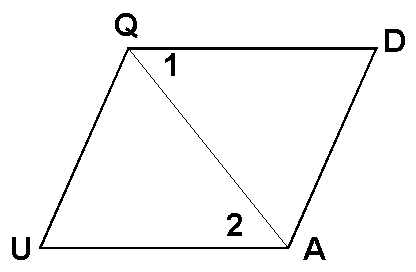
Given: line QD not || line UA
Prove: Ð1 not @ Ð2
Paragraph proof: Assume Ð1 @ Ð2 (indirect proof). Then line QD || line UA since alt. int. Ðs @ Þ || lines, a contradiction. Q.E.D.
Alternate "quickie" proof: We have the contrapositive of the "alt. int. Ðs @ Þ || lines" theorem. Q.E.D.
Two-column proof:
1. Assume Ð1 @ Ð2
1. For pf. by contrad. (negation of concl.)
2. line QD not || line UA
2. Given
3. line QD || line UA
3. From step 1, by alt. int. (contradicts step 2, Q.E.D.)
14.
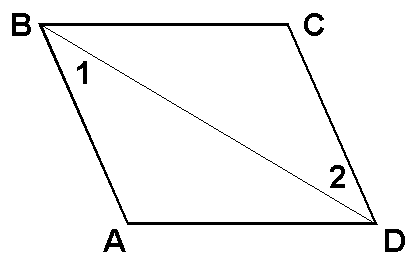
Given: sAB @ sCD, sBC @ sAD
Prove: sAB || sCD
1. sAB @ sCD, sBC @ sAD
1. Given
2. sBD @ sBD
2. Refl.
3. DBAD @ DDCB
3. SSS (steps 1, 2)
4. Ð1 @ Ð2
4. CPCTC
5. sAB || sCD
5. Alt. int. Ðs @ Þ ||
15.
mPQ = Dy/Dx = (4 – 1)/(2 – (–3)) = 3/5
mRS = Dy/Dx = (2 – (–2))/(7 – 1) = 4/6 = 2/3 ¹ mPQ
Segments are not parallel since their slopes are unequal.
16.
By vert. Ðs, 5x – 20 = x + 84
4x = 104
x = 26
\ x + 84 = 26 + 84 = 110
Since the Ð marked (x + 84)° is a corresp. Ð to the one marked 110°, and since these corresp. Ðs are @, m || n as claimed.
17.
As you discovered in the very beginning of Sketchpad Lab IV, an exterior Ð of a D always exceeds either of the remote interior Ðs. (In fact, the ext. Ð equals the sum of the remote int. Ðs.) We also know that the exterior Ð must be less than 180° since all Ðs involved with Ds are less than a straight Ð.
\ 30 < 3x – 18 < 180
48 < 3x < 198
16 < x < 66
18.
x = 14.5 Þ marked Ðs are 116° and 64°, respectively
\ we have int. Ðs on SSOT being supp., which means p || q
19.
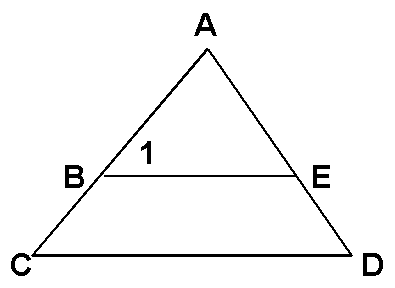
Given: ÐD @ Ð1, sBE not || sCD
Prove: AC ¹ AD
1. Assume AC = AD
1. For pf. by contrad. (negation of concl.)
2. sBE not || sCD
2. Given
3. ÐC @ ÐD
3. ITT
4. ÐD @ Ð1
4. Given
5. ÐC @ Ð1
5. Trans.
6. sBE || sCD
6. Corresp. Ð s @ Þ || (contradicts step 2, Q.E.D.)
22.
Since ÐLPM is an ext. Ð to DLKP, x > 81.
But more is true: Since the supp. of ÐLPM is an ext. Ð to DLPM,
180 – x > 37
180 – 37 > x
143 > x
x < 143.
To summarize, 81 < x < 143.
23.
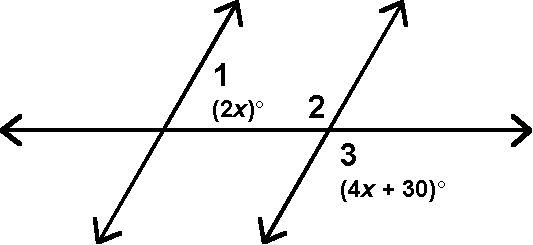
If x were 25, mÐ1 = 50 and mÐ3 = 130. But Ð2 @ Ð3 (vert. Ðs), so Ð2 supp. Ð1. That would force the diagonal lines to be ||, since you discovered at the end of Sketchpad Lab IV that int. Ðs SSOT supp. Þ
||.
Since the diagonal lines were given to be not parallel, we have a contradiction. What can we say? Clearly, x cannot be 25.