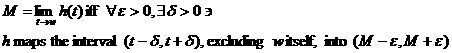Test #1 (Chapters 1 & 2), 9/24/2002

Honors AP Calculus / Mr. Hansen
9/24/2002

Name: ____________________
Test #1

Test on Chapters 1 and 2

Today’s test begins the long challenge of preparing you for the AP exam on Thursday, May 8, 2003. This test is like the AP exam in the following respects:

You may not use calculator notation in your written work. For example, you must write dy/dx or f¢ notation instead of nDeriv.
No questions will be taken once the test has started. If you believe you have found a misprint, answer the question to the best of your ability and indicate clearly what assumptions you are making in the problem in order to continue working.
If you make a mistake, you may mark an “X” through it instead of erasing. Work marked with an “X” will be ignored during grading.
Multiple choice: Work is not required in this section, but there is also no partial credit. Use any ethical means at your disposal, including any features available on your calculator, to answer the questions.
Free response: Show sufficient work and write legibly. Work systematically, one thought per line, so that the thrust of your argument is clear and logical. Circle answers and give units (ft., cm, etc.) if appropriate. Decimal answers should be rounded only at the very end and should be accurate to at least 3 places.
The test is too long to be completed in the time provided. Work as many problems as you can, and let the rest go. Do not guess, since guessing tends to be a waste of time and can certainly hurt you in the multiple-choice section, where there is a point penalty for each wrong guess. (If you can positively eliminate one or more choices, random guessing from among those that remain can help you. However, I have rarely known students who were willing to employ truly random guessing. By making “educated guesses,” they nearly always get the wrong answer.)
Time will end promptly at the end of the period. No work after that time will be graded.
You can miss some problems and still earn a high score.

This test is unlike the AP exam in the following respects:

The multiple-choice and free-response sections, instead of being weighted equally, are approximately 1/3 and 2/3 of this test, respectively.
In the interest of efficiency, we will not switch back and forth between “calculator not allowed” and “calculator allowed” sections. You may use your calculator, and anything stored in it, for the entire test.
Although the AP exam enforces separate time limits for the multiple-choice and free-response sections, you may subdivide your time today as you see fit. However, do not take much more than about 2 minutes, on average, for each multiple-choice question. In other words, you should allow more than half of your time today for the free-response portion.

Final thoughts:

Points will be rescaled to 100 points in order to recognize the length and difficulty of the test.
The test is long and hard. You do not need to tell me that, because I know it. Please have faith that there is a purpose (namely, training you for the AP examination) and that the scoring will be adjusted in an educationally sound manner. Historically, a large majority of my HappyCal students have earned grades of B+, A, or A+ for the course.

Honors AP Calculus / Mr. Hansen
9/24/2002

Please print your
name only on the cover sheet.

Test on Chapters 1 and 2

	Part I: Multiple Choice. 2 pts. for each correct answer, ½ pt. penalty for each wrong guess, 0 pts. for each omission
1.	Which of the following must be true if f is a continuous function of x for all x Î Â, f ¢¢(2.9) = –2, and f ¢¢(3.1) = 4.28? I. The point x = 3 is a point of inflection for f. II. Function f is differentiable at x = 3. III. Function f ¢ is differentiable at x = 3. A) I only B) I and II only C) I and III only D) I, II, and III E) none of the above

2.	equals A) the right-handed derivative of G at 2 B) the right-handed derivative of G at q C) G ¢(2) D) G ¢(q) E) none of the above

3.	If g is a continuous function of x for all x Î Â, then an antiderivative of g is A) the unique function G(x) such that B) any function G(x) such that , where any two possible candidates for G differ by a constant C) the unique function G(x) such that D) any function G(x) such that , where any two possible candidates for G differ by a constant E) none of the above
4.	The trapezoidal rule estimate of that uses 5 equally spaced subintervals (i.e., 6 mesh points) is A) 15.520 B) 23.254 C) 24.178 D) 25.822 E) 26.304

5.	Use your calculator’s numeric integration feature to calculate the expression in #4 to the nearest whole unit. (Hint: You will save time by computing only the accuracy requested.) A) 23 B) 24 C) 25 D) 26 E) 27

6.	Problems 4 and 5 are both examples of A) quadrature B) adaptive quadrature C) numeric differentiation D) symbolic differentiation E) antidifferentiation

7.	Suppose that for all x Î [a, b], f (x) > 0, f ¢(x) < 0 and f ¢¢(x) > 0. Which of the following must be true concerning S = ? I. The trapezoidal rule underestimates S regardless of the number of mesh points. II. The right endpoint rule overestimates S regardless of the number of mesh points. III. The right endpoint rule underestimates S regardless of the number of mesh points. A) I only B) II only C) III only D) I and II only E) I and III only

8.	The function y = x^2/3 has A) no cusps and no points of inflection B) no cusps and one point of inflection C) no cusps and two points of inflection D) one cusp and no points of inflection E) one cusp and one point of inflection

9.	What is wrong with the following definition of limit? A) Nothing is wrong; the definition is acceptable as it stands. B) The source interval (t – d, t + d) is wrong. It should be (w – d, w + d). C) The phrase “excluding w itself” is invalid. The definition must include the value of w itself. D) The destination interval (M – e, M + e) is wrong. It should be (h(w) – e, h(w) + e). E) The destination interval (M – e, M + e) is wrong. It should be (h(t) – e, h(t) + e).

10.	Consider the function for x ¹ 2, and define f (2) = 0. Which of the following are true? I. f is differentiable at x = 0 II. f has a left-handed limit at x = 0 III. f has a right-handed limit at x = 0 IV. f has a two-sided limit at x = 0 A) I only B) II only C) III only D) II and III only E) I, II, III, and IV

11.	If there exist values x₁ and x₂ within closed interval [a, b] such that f (x₁) is the maximum value of f on [a, b] and f (x₂) is the minimum value of f on [a, b], then which of the following must be true? I. f (x₁) > f (x₂) II. f (x₁) ³ f (x₂) III. f ¢(x₁) = f ¢(x₂) = 0 IV. f is continuous on [a, b] A) I only B) II only C) I and III only D) II and III only E) II, III, and IV only

	Part II: Free Response.
12.	Let P(x) = x³.
(a)	P is an example of a ____________ function.
(b)	Using the mechanical rule we learned in class, write an equation that states P ¢(x) for any x.

(c)	Use the limit definition of derivative to compute P ¢(2). Show all work. If you have forgotten how to factor a difference of cubes, you may compute P ¢(x) instead, using the limit definition, and plug in 2 at the end.

















(d)	Make a rough sketch of P and show that your answer to (c) is reasonable as a slope. If you could not solve (c), use (b) to compute P ¢(2) and use that value in your sketch.










(e)	Is the origin a point of inflection for P? Why or why not? (Write approx. 2 sentences.)





(f)	Write equations for P(1.55) and P(1.56). (No work needed.)

(g)	Use the result of part (f) as follows. Turn off your calculator and use a theorem we learned to estimate to the nearest tenth. ___________ What theorem are you using? ______________ Hint: Since P is continuous on [1.55, 1.56], and since 3.75 is between _____ and _____ , we know i.e., ___________ = .

13.	Let r(t) be a continuous function of t .
(a)
(b)
(c)
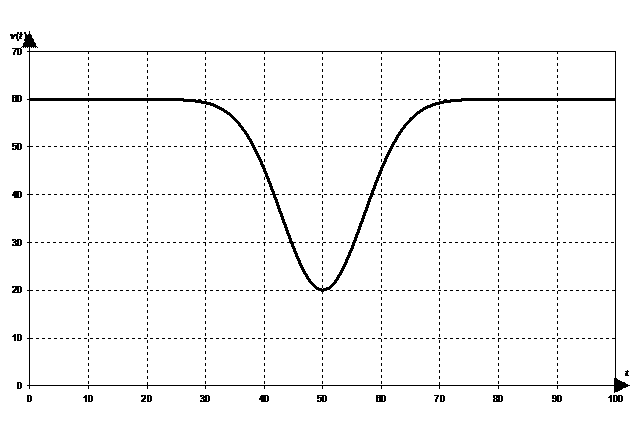
14.	The velocity of a car, v(t), in feet per second, is given by the graph below for time t measured in seconds.

(a)	How far did the car travel between t = 0 and t = 20 seconds? ______________
(b)	About how far did the car go between t = 30 and t = 70 seconds? ________________ What core concept of the calculus (one of the four main topic areas) is used to find this distance? ________
(c)	Tell what might have happened in the real world to make the car’s velocity-time graph look this way.



(d)	At time t = 60 seconds, was the car speeding up or slowing down? ____________ At approximately what rate? __________________________
(e)	Shortly after t = 100 sec., the driver is pulled over by a state trooper and ticketed for exceeding the posted speed limit of 40 mph (58 2/3 ft./sec.) during the interval 30 £ t £ 70. The driver objects and argues—based on part (b)—that his average velocity in the interval [30, 70] was much less. What is that average velocity? __________________________ (If you couldn’t get part (b), use 2000 ft. as an estimate for part (b).) Explain (in 1-2 sentences) whose argument is more valid, the trooper’s or the driver’s.