|
Honors AP Calculus / Mr. Hansen |
Name: _________________________ |
Test on Chapter 8
Instructions are the same as always, with one small modification.
- Today only, there will be partial credit awarded in the multiple choice section if you show your work. (This is because of the power failure that made it impossible to duplicate the entire test.)
- The sequence today will be 5 modified multiple-choice (as described above), 1 free-response question with calculator, and 1 free-response question without calculator (during which you may continue to work on both problems).
- You may use your calculator only during the first 30 minutes of the test.
- In free-response questions, justify steps and use standard math notation—not calculator notation.
- Work top to bottom, left to right, and write legibly.
- Mark with a single neat “X” any portion you wish to be ignored during grading. (Do not waste time with large erasures.)
- No questions will be taken once the test has started. If you believe you have found a misprint, answer the question to the best of your ability and indicate clearly what assumptions you are making in the problem in order to continue working.
- Time will end promptly at the end of the period. No work after that time will be graded.
- You can miss some problems and still earn a high score.
|
|
Section I: Multiple
Choice, CALCULATOR REQUIRED. Time limit: 15 minutes. |
|
|
1. |
Compute the area bounded by the curve xy = 4, the x-axis, x = e, and x = 2e. |
|
|
|
(A) 4.000 |
(D) 1.386 |
|
|
|
|
|
2. |
Compute the volume of the solid formed when the triangle defined by x = 3 and y = 8 ± 2x is revolved about the y-axis. |
|
|
|
(A) 17.5p |
(D) 70p |
|
|
|
|
|
3. |
Sketch a function that is continuous everywhere, has undefined derivative at x = 0, is increasing for x < 0 and 0 < x < 3, has inflection points at x = 0 and x = 2, and has a local max. at x = 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
For questions 4 and 5, consider the region in Quadrant II that lies between the first and second thread of the spiral r = 0.04e0.15q as it works outward. |
|
|
|
|
|
|
4. |
Compute the total length (all 4 pieces) of the region’s boundary. |
|
|
|
|
|
|
5. |
Compute the region’s area. |
|
|
|
Section II, Part A: Free Response, CALCULATOR REQUIRED. Time limit: 15 minutes. |
|
|
|
|
6. |
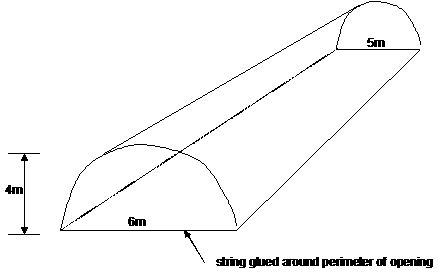
A 2000m tunnel having parabolic cross section is to be dug
through solid rock, following a straight path. At one end of the tunnel, the
opening has width 6m and height 4m. At the other end, the height is still 4m,
but the width is 5m (tapering in a linear fashion with respect to the length
of the tunnel). |
|
|
|
|
(a) |
Prove that the symmetric area inside a quadratic parabola of finite height equals 2/3 the length of the base (i.e., the distance between the “prongs”) times the height. Hint: You may wish to create a generalized parabola of the form y = c1x2 or, if you prefer, you may consider the area under the curve y = c2 – c3x2. (The ci denote positive constants. You may use other letters if you wish.) |
|
(b) |
Apply the result of (a) to show that the cross-sectional area of the tunnel has a mean value of 44/3 m2. [Remember, especially when you take the AP exam, that you can do this even if you were unable to answer part (a)!] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c) |
A piece of string is glued along the parabolic sides and flat bottom of the tunnel at the 6m-wide entrance. Compute the total length of the string. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(d) |
Compute the total volume of rock removed in constructing the tunnel. |
|
|
Section II, Part B:
Free Response, NO CALCULATOR PERMITTED. Time limit: 15 minutes. |
|
7. |
A long, flat, rectangular piece of sheet metal is to be fashioned into a V-shaped trough to carry rainwater. The width of the rectangle is 6 inches, and the length is more than 12 feet. Your task is to crease the rectangle in half lengthwise (forming two flaps of 3 inches each) in such a way that the water-carrying capacity of the V-shaped metal that results is maximized. This will be accomplished, in other words, by maximizing the area of the cross-section, which is an isosceles triangle having two legs of length 3 and a third leg (the length of the opening between the “points” of the V) of unknown length. |
|
|
|
|
(a) |
Write a function A(x) that expresses the cross-sectional area as a function of the length x of the unknown side. Justify your function with a diagram or other suitable work. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b) |
Sketch the graph of A(x) and indicate what the suitable domain for x is. |
|
(c) |
Find the global maximum possible cross-sectional area, and give your answer in square inches. Justify your conclusion analytically. Although you may refer to your graph in part (b) to guide your thinking, your justification must be completely supported through non-graphical means. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(d) |
Show that for any long rectangular piece of sheet metal fashioned into a V shape as in this problem, the maximum cross-sectional area occurs when the opening is w/Ö2, where w denotes the original width of the piece of sheet metal. |