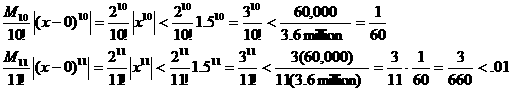Honors AP Calculus / Mr. Hansen
4/17/2003

Name: _________________________

Quiz/Check for Understanding on Chapter 12
Explanation of Question 2(b)

2.

Ungraded question (approx. 3 minutes).

 

 

(b)

Show that for –1.5 < x < 0, the error when estimating sin 2x by using 5 nonzero terms of your series in #1(a) is always less than .01 in absolute value.

 

 

Hints

310 < 60,000
10! > 3.6 million

 

 

KEY

The appropriate way to solve this problem is by using the alternating series error bound. We did this in class, and it was fairly quick and straightforward.

However, we encountered difficulty when a few students asked (innocently) what would be involved in using the Lagrange form of the remainder. I said, “Believe me, it’s a lot more work,” and then instead of moving on, I unwisely plunged right in and entered a festering swamp.

The problem can be solved using the Lagrange form, but you need to consider the situation more carefully than I did in class.

Let f (x) = sin 2x. Clearly Mn = 2n is an upper bound for the magnitude of the nth derivative, regardless of the value of the argument.

It may help, when visualizing the problem, to write out several terms of the Maclaurin series for f (x), namely

f (x) = f (0) + f ˘(0) · (x – 0) + f ˘˘(0)/2! · (x – 0)2 + f ˘˘˘(0)/3! · (x – 0)3 + . . .

Because of the way the derivatives of sin 2x work out, every even-degree term of this series is actually 0, and because x < 0 (given), the odd-degree terms are all nonzero.

Since we are to use 5 nonzero terms (given), the Maclaurin term involving x9 is the last nonzero one that we are using. Since the Maclaurin term involving x10 is 0, we have a choice for our Lagrange error bound of using eithe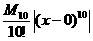r  or .

 

 

 

 

 

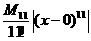We prefer the latter, since by inspection, the Lagrange error bound using M11 will be smaller.

But just for fun, let’s go ahead and compute both error bounds. Using the hints provided on the board (310 < 60,000 and 10! > 3.6 million) and no calculator, we have

 

 

 

 

 


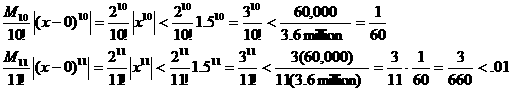
It is interesting to note that the first Lagrange error bound is not “tight” enough to solve the problem as posed, but the second one works nicely and in fact is numerically equal to the AST error bound.