|
1.
|
∫e2e
4/x dx = 2.773 by calc. (choice C).
|
|
2.
|
Washer method: V
= ∫28 p(R2
r2)dy + ∫814
p(R2 r2)dy. By symmetry, these are actually equal, so we can say V = 2∫814 p(R2 r2)dy = 2p∫814
(32 (y/2 4)2)dy = 2p(36)
by calc.
Shell method: V = ∫03
2prh dx = ∫03
2px((8 + 2x) (8 2x)) dx
= 2p∫03
x(4x) dx
= 2p(36)
by calc. or FTC.
Answer: 72p
(choice E).
|
|
3.
|
Many answers are possible. Normally you would have been
given 5 plausible choices and forced to reject all but one.
Here is an example that satisfies the conditions of the problem as stated but
has an additional place (namely x =
3) where the derivative is undefined:
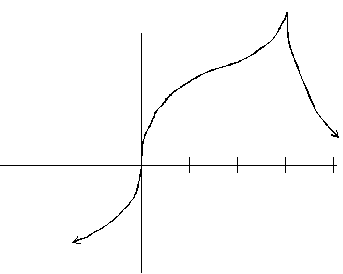
Here is another example that satisfies the conditions of the problem, except
this time there is an extra point of inflection somewhere between x = 2 and x = 3:
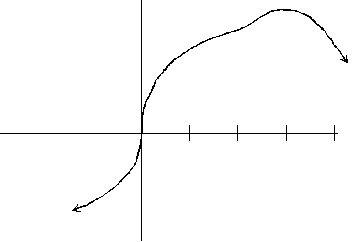
Finally, here is an example that satisfies the conditions of the problem
without having any extra features:
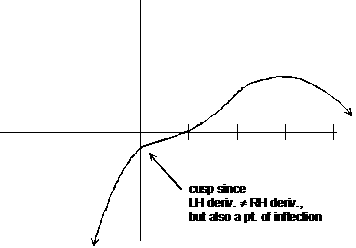
|
|
4.
|

The shaded region is bounded by two polar arcs and two line segments. The
polar arcs have length ∫p/2p
((dr/dq)2
+ r2)1/2 dq + ∫5p/23p
((dr/dq)2 + r2)1/2 dq = .090679... + .2327...
by calc. The exact keystrokes are as follows,
assuming you have already stored .04e.15q
into the r1 polar function:
fnInt(ึ(nDeriv(r1,q,q)2+r12),q,p/2,p)
to get .090679...
fnInt(ึ(nDeriv(r1,q,q)2+r12),q,5p/2,3p)
to get .2327...
For speed, you should enter the first one, store the result into a variable
such as A, and then use 2nd ENTRY to edit the second one without retyping.
Clearly, knowing how to use your calculator effectively is the main skill
here.
If you wish to use FTC, though you really shouldnt, (dr/dq)2 + r2
= .000036e.3q
+ .0016e.3q
= .001636e.3q,
which has a square root of .040447...e.15q,
which in turn has an antiderivative of .2696...e.15q.
Letting c = .2696..., we have c(e.15q)|p/2p
for the first polar arc length and c(e.15q)|5p/23p
for the second. These give the same values as the calculator results found
above. In a free-response question, you should show the integrand as the
square root of .001636e.3q
so that the grader can tell you know what youre doing, but on a
multiple-choice question that would be a waste of time.
For the two line segments, we need only compute the differences between the
polar radii, i.e., r1(5p/2)
r1(p/2)
and r1(3p) r1(p). These lengths are
.079... and .100369..., respectively. Adding all
four lengths gives .503 as the final answer.
|
|
5.
|
By the polar area formula, A = ∫5p/23p
r2/2 dq ∫p/2p
r2/2 dq = .0169... .00257...
= .014 by calc. Again, you could do this by FTC, but on a
multiple-choice question you would be wasting your time.
Reasonableness check: A ป
quarter circle of radius .15 = p(.15)2/4 = .018.
|
|
6.(a)
|
We did this in class. Here is a slightly different method
in the same general vein:
Wlog, let y
= ax2 be the parabola,
where a < 0. Parabola opens downward,
and if we go symmetrically outward from the origin ฑb units, where b >
0, the positive area above the parabola is ∫bb ax2 dx = 2∫0b ax2 dx = 2ax3/3|0b = 2ab3/3, which we can rewrite as |2ab3/3|. The area of the bounding rectangle is the width,
2b, multiplied by the height. Since
height is the absolute value of the y-value
of the parabola when x = ฑb, height is |ab2|, giving a rectangular area of |2ab3|. Since we showed
earlier that the area above the parabola is 1/3 of this, the area below the
parabola is 2/3 of this. Q.E.D.
|
|
(b)
|
Since width w
tapers linearly from 6 to 5, w =
5.5 at tunnels midpoint. By part (a), A
= 2/3wh = 2/3 ท 5.5 ท 4 = 44/3 m2
as claimed.
|
|
(c)
|
Easiest way is to place the origin at the midpoint of the flat
part of the opening. The tunnels arch then follows the parabolic function y = 4 cx2, where c
> 0 is a constant. You may be able to find c by inspection, but it is better to show your work: since y = 0 when x = 3, 0 = 4 9c,
which gives c = 4/9. Bottom part of
string is 6m by inspection, and the upper curved part is found by arc length
formula: ∫33(1 + (dy/dx)2)1/2 dx = ∫33(1
+ (dy/dx)2)1/2
= ∫33(1 + (2cx)2)1/2
= ∫33(1 + 4c2x2)1/2 =
10.4648...
Final answer: 10.4648... + 6 = 16.465 m.
|
|
(d)
|
V = ∫02000A(x)
dx where A(x)
= 2/3 wh
and w is a linear function of x. By inspection,
w = 6 x/2000.
If you wish to show more work, use the conditions w(0) = 6, w(2000) = 5 to develop the point-slope form of the linear
equation, namely
w w0 = (5 6)/(2000 0) ท (x x0).
This simplifies to w 6 = 1/2000
ท (x 0), or w = 6 x/2000 as
claimed above.
Plugging in, we have V = ∫02000(2/3 wh) dx = ∫02000(2/3
(6 x/2000) 4) dx = 29333.333 m3.
Fast alternate method [preferred]: Since w
varies linearly, cross-sectional area varies linearly. Thus the volume is
simply the length of the tunnel multiplied by the mean cross-sectional area
from part (b). We have V =
2000(44/3) = 29333.333 m3.
|
|
7.(a)
|
In an isosceles triangle of sides 3, 3, and x, where x< 6, altitude is h
= (32 (x/2)2)1/2
by Pythag. Thm. This
simplifies to h = (9 x2/4)1/2. By the
formula A = ฝ bh, we have
A(x) = .5x(9
x2/4)1/2.
|
|
(b)
|
Domain is 0 < x
< 6. Plug in integer values 0, 2, 4, and 6 to get a sense of the shape (a
rough sketch is clearly acceptable since this is a non-calculator section).
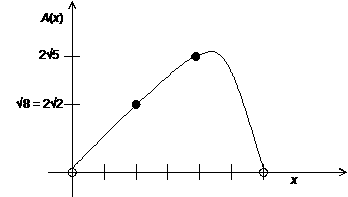
A(0) = .5(0) (9 x2/4)1/2 = 0
A(1) = .5(1) (9 12/4)1/2
= .5ึ8.75
A(2) = .5(2) (9 22/4)1/2
= 1ึ8
A(3) = .5(3) (9 32/4)1/2
= 1.5ึ6.75
A(4) = .5(4) (9 42/4)1/2
= 2ึ5
A(5) = .5(5) (9 52/4)1/2
= 2.5ึ2.75
A(6) = .5(6) (9 62/4)1/2
= 3(0) = 0
|
|
(c)
|
[There are many ways to work this problem, but one thing
you should not do is to try the
second derivative test. The algebra quickly becomes daunting.]
Assertion: There is only one place on the domain D = (0, 6) where dA/dx can change
sign.
Proof: By logarithmic differentiation, dA/dx
= A/x Ax/(36 x2).
[You need to show the steps.] We can rewrite this as dA/dx
= Ax(1/x2 1/(36 x2)), which clearly takes
its sign only from the second factor since Ax > 0 on D.
Let us analyze the second factor by comparing p = 1/x2 to q = 1/(36 x2). The derivative dA/dx is positive iff p > q iff x2 < 36 x2 iff
2x2 < 36 iff |x| < 3ึ2.
Similarly, dA/dx = 0 iff
p = q iff x = 3ึ2,
and dA/dx < 0 iff
p < q iff |x| > 3ึ2. Thus x =
3ึ2
is the only place in D at which a sign change can occur. Q.E.D.
In the process of proving that assertion, we also established that x = 3ึ2 gives a global max.
A(3ึ2)
= .5(3ึ2)
(9 (3ึ2)2/4)1/2
= (1.5ึ2)
(9 18/4)1/2 = 4.5 in2 by algebra.
[Simplification is not required, but you should include the units.]
[Note that if we peeked ahead to part (d), which is never a bad idea when
working an AP exam, we would know that x
= 6/ึ2,
which simplifies to 3ึ2, would provide our global max. That at least tells
us in what direction the solution lies.]
|
|
(d)
|
If you replace all occurrences of 6 in the original
problem with w, and if you repeat
the logarithmic differentiation as in part (c), you can show that dA/dx = Ax(1/x2 1/(w2
x2)) for x ฮ (0, w). The algebra is actually easier
with the parameter of w, as long as
you remember that w is not a
variable. By a similar analysis as the one used in part (c), dA/dx changes sign only once on
(0, w), in fact from positive to
negative, when x = w/ึ2. Therefore, x = w/ึ2
creates the maximum cross-sectional area. [Steps omitted.]
There is also an interesting non-calculus way of getting this. Observe that to
maximize the area of the triangular cross section, it suffices to maximize
the area of the following right triangle:
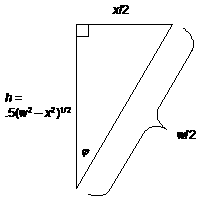
You may recall from geometry that area can be maximized by adjusting the
angle j
shown in the diagram. To see how, let us add an auxiliary perpendicular line,
an altitude of length a:
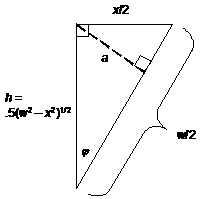
Now, sin j
= a/h and cos j = h/(w/2) = 2h/w.
Therefore, sin 2j
= 2 sin j
cos j = 2(2a/w) = (4/w)a,
which is simply a positive constant times a.
Let us say sin 2j
= ka, k > 0.
Maximizing the area of the large right triangle (if we view the base as being
the long side w/2 and the altitude
as a) involves a fixed base and an
adjustable altitude, so clearly we should maximize a if we wish to maximize area.
But maximizing a is
equivalent to maximizing ka in our
expression for sin 2j, and by inspection sin 2j is maximized when j = p/4.
That makes h = x/2, since we have an isosceles right triangle.
Since h = .5(w2 x2)1/2
by Pythag. Thm., we can solve the equation h = x/2 for x to get x = w/ึ2
as claimed.
|






