|
T 9/1/15
X
|
First day of class.
|
|
|
W 9/2/15
A
|
HW due: Send Mr. Hansen an
e-mail. (Refer to the contact information page
if you have forgotten the address.)
|
|
|
Th
9/3/15
B
|
HW due:
§0.1 (pp. 15-17) #1-8 all, 16, 20, 32, 38, 40, 52, 54, 64, 68, 78, 84, 88
§0.2 (pp. 25-27) #4, 6, 12, 20, 32, 38, 42, 72
§0.3 (pp. 35-37 #4, 12, 28
|
|
|
F 9/4/15
C
|
No class.
|
|
|
M 9/7/15
|
No school (Labor Day).
|
|
|
T 9/8/15
D
|
HW due:
§0.1 (pp. 15-17) #40, 68, 86
§0.2 (pp. 25-27) #30, 40, 46, 50, 74
§0.3 (pp. 35-37) #20, 32, 44, 56, 68, 76, 78
§0.4 (pp. 46-48) #12
|
|
|
W 9/9/15
E
|
HW due:
§0.3 (pp. 35-37) #24, 54, 64
§0.4 (pp. 46-47) #14, 26, 48, 66, 80
|
|
|
Th 9/10
15
F
|
No class.
|
|
|
F 9/11/15
G
|
HW due:
§0.3 (pp. 35-37) #62, 80
§0.4 (pp. 46-48) #32, 40, 50, 54, 64, 78, 86
§0.5 (pp. 60-61) #8, 16, 36, 40
|
|
|
M 9/14/15
A
|
HW due:
§0.5 (pp. 60-61) #6, 22, 28, 38, 48, 54, 66, 72, 80
§0.6 (pp. 71-73) #2, 12, 18, 26
|
|
|
T 9/15/15
B
|
HW due:
§0.5 (pp. 60-61) #26, 44, 64, 70, 82
§0.6 (pp. 71-73) #8, 20, 34, 44, 48, 54, 60, 64
|
|
|
W 9/16/15
C
|
No class.
|
|
|
Th
9/17/15
D
|
HW due:
1. Bring at least 3 good questions to class (can be from the book or from
your own mind). Questions must be written out, just like a standard HW question,
except that you can leave the answer blank.
2. Start working on §1.1 (pp. 97-99) #16, 22, 24, 26, 32, 34, 36, 42, 44, 48,
54, 60, 64, 70. These problems will be collected next Tuesday.
In class: Review.
|
|
|
F 9/18/15
E
|
Test on Unit 0 (§0.1–§0.6)
|
|
|
M 9/21/15
F
|
No class.
|
|
|
T 9/22/15
G
|
HW due:
§1.1 (pp. 97-99) #16, 22, 24, 26, 32, 34, 36, 42, 44, 48, 54, 60, 64, 70
(assigned last week)
§1.2 (pp. 110-113) #4-32 mo4
Note: “mo4” means “multiples of 4.”
|
|
|
W 9/23/15
A
|
HW due:
§1.1 (pp. 97-99) #30, 46, 52, 62
§1.2 (pp. 110-113) #6, 18
§1.3 (pp. 124-127) #10, 28, 62, 84
|
|
|
Th
9/24/15
B
|
HW due:
§1.2 (pp. 110-113) #22, 30
§1.3 (pp. 124-127) #32, 38, 46, 52, 66, 74, 76, 88
§1.4 (pp. 133-135) #2, 20, 26
|
|
|
F 9/25/15
X
|
Before school (7:00 a.m.): Optional Re-Test on Unit
0. If you choose to take this test,
and if your score is higher than your original score, some points will be
added to your final recorded score. (The weighting scale will be determined
later.) For example, if your original score was 59 and your re-test score is
89, you can count on having a passing score recorded. The 89 will not be
recorded, but it is a safe bet that something in the 70s will be recorded as
your final score, and that’s a lot better than 59.
If your re-test score is less than or equal to your original score, your
original score will be kept. In other words, the re-test cannot hurt you.
The re-test will end promptly at 7:36
a.m. (regular time) or 7:54 a.m. (extended time).
In order to prepare for the re-test, you should work through many of the
review problems at the end of Unit 0. Odd-numbered problems are best, because
the answers are found on p. 1200. (Note that #51 is essentially the same as
#12 on your test, with letters changed.) If you need more practice problems
of a certain type, go back to §0.1 through §0.6 in the textbook, and work
some of the odd-numbered problems found there. If you need more basic review
practice from Algebra I, additional practice and on-line quizzes are available
here.
HW due:
§1.3 (pp. 124-127) #8, 48, 56, 80, 92, 106
§1.4 (pp. 133-135) #22, 24, 34, 42, 62
§1.5 (pp. 142-145) #10, 38, 58, 64, 72
|
|
|
M 9/28/15
C
|
No class.
|
|
|
T 9/29/15
D
|
HW due:
§1.4 (pp. 133-135) #18, 30, 36
§1.5 (pp. 142-145) #16, 44, 56, 68, 82
§1.6 (pp. 154-156) #10, 24, 34
|
|
|
W 9/30/15
E
|
HW due:
§1.5 (pp. 142-145) #84, 92, 108
§1.6 (pp. 154-156) #18, 28, 32, 40
§1.7 (pp. 161-163) #10, 18, 34, 44, 48
|
|
|
Th
10/1/15
F
|
No class.
|
|
|
F 10/2/15
G
|
HW due:
§1.6 (pp. 154-156) #16, 20, 30, 36, 38, 64
§1.7 (pp. 161-163 #20, 28, 30, 40, 52, 58, 76
|
|
|
M 10/5/15
A
|
HW due:
Review (pp. 166-169) #8, 16, 22, 30, 38, 42, 46, 48, 54, 62, 68, 72, 80, 92,
108, 114, 122, 128, 130, 138, 140, 144
|
|
|
T 10/6/15
B
|
HW due:
§2.1 (pp. 178-182) #8, 18, 22, 46
|
|
|
W 10/7/15
C
|
No class.
|
|
|
Th
10/8/15
D
|
Test on Unit 1 (§1.1–§1.7)
As you prepare for the test (by working review exercises and the practice
test at end of Chapter 1), be sure to keep older material in mind. The
cumulative test on p. 171, excluding question #12, may be helpful to you.
|
|
|
F 10/9/15
|
No school (faculty
professional day).
|
|
|
M 10/12/15
|
No school (Columbus Day).
|
|
|
T 10/13/15
E
|
HW due:
§2.1 (pp. 178-182) #23, 29, 47
§2.2 (pp. 189-193) #4, 12, 20, 31, 33-38 all, 52, 62
§2.3 (pp. 205-209) #4, 24, 38
|
|
|
W 10/14/15
F
|
No class.
|
|
|
Th
10/15/15
G
|
HW due: “Half-back” test
corrections. Detailed instructions are given below. Everyone is required to
do these, even those students who had good scores on the test itself. Here is
an optional blank copy of
the Oct. 8 test in case yours is too marked-up to be legible.
Detailed Instructions:
1. Rewrite the answers for all
problems from page 1, regardless of whether or not you got them correct, on
the back of page 5. Rewrite the answers for all problems and work from page 2
on the back of page 4. Rewrite the answers for all problems and work from
page 3 on the back of page 3. Rewrite the answers for all problems and work
from page 4 on the back of page 2. Rewrite the answers for all problems and
work from page 5 on the back of page 1. Therefore, your corrected test will
read, in order, as you leaf from the back of page 5 to the back of page 1.
2. If you wish, you may disassemble your test so as to facilitate seeing the
problems and your work at the same time. However, if you do that, be sure to
re-staple your test in the upper left-hand corner of page 1 when you are
finished (i.e., in the original
configuration of the test).
3. You do not need to rewrite the questions for the multiple-choice questions
(and essay question, if you have one). Answers are sufficient.
4. For free-response questions (namely, questions 8 through 15), you do not
need to restate the entire question. However, you must write the starting equation or inequality.
5. Number all corrections, and work neatly. You must conform to the rules for
writing digits 0-9 and the “quite sizzly” rules for
variables.
6. Working with friends is permitted for
this assignment only. However, you must acknowledge their contribution.
Example: “Thanks to Fred S. for explaining why I had to set eqn. equal to 0.”
7. Your work will be spot-checked. If it passes the spot check, you will be
awarded 50% of your lost points. However, if any problem is found deficient during the spot check, the entire
test will be rejected. In the event of a rejection, you will still qualify
for some bonus points, but it may not be a full “half-back” bonus, and you
will have to present your corrections in person to Mr. Hansen (after school
or by appointment) until your corrections are completely correct.
|
|
|
F 10/16/15
A
|
HW due:
§2.2 (pp. 189-193) #3, 11, 19, 51, 61
§2.3 (pp. 205-209) #3, 23, 37
|
|
|
M 10/19/15
B
|
HW due:
1. Read §3.1 (pp. 226-238). Reading notes are required. (See the “HW
guidelines” link at top of schedule.)
2. Solve the following problems:
§2.1 (pp. 178-182) #49-52 all
§2.2 (pp. 189-193) #77, 79, 80, 81
§2.3 (pp. 205-209) #43-50 (oral preparation only—do not write anything for
these)
§2.3 (pp. 205-209) #51, 53, 55, 108
§2.4 (pp. 214-217) #1, 7, 47, 49
|
|
|
T 10/20/15
C
|
No class.
|
|
|
W 10/21/15
D
|
HW due:
Write: pp. 220-221 #1, 3, 9, 11, 15, 16, 24, 26, 29, 40, 45, 51, 55, 57, 71.
Prepare orally (do not write): p. 220 #35-44 all, p. 222 #19-20.
Write: p. 222 #5, 10, 12, 13, 15.
Write: p. 223 #2, 13, 16, 18, 19, 20.
Write p. 240 #45, 53.
If you cannot finish all the problems, do as many as you can and keep a time
log. (Then, do any remaining problems as part of your studying on Wednesday
night.)
In class: Review. We will cover all the even-numbered HW problems first,
followed by as many odd-numbered problems as possible.
|
|
|
Th
10/22/15
E
|
Test on Unit 2 (§§2.1–2.4)
Problems will be similar to those found on pp. 220-223, with the addition of
(1) at least one problem designed to see if you know what the square root of x2 is and (2) at least one
seemingly difficult problem that can be solved by inspection. Format will be
similar to the format of the Oct. 8 test (multiple choice and free response).
|
|
|
F 10/23/15
F
|
No class.
|
|
|
M 10/26/15
G
|
HW due:
1. Read §3.2 (pp. 244-258). Reading notes are required.
2. Write §3.1 (pp. 239-241) #1-14 all, 19-24 all, 31abc, 41-55 odd.
3. Prepare orally (do not write) #65-81 all in §3.1.
|
|
|
T 10/27/15
A
|
HW due:
1. Correct last week’s
test. Since this is not for “half-back” credit, you do not need to redo
the problems that you answered correctly. However, please use the same format
as before: corrections for page 1 on the back side of page 5, corrections for
page 2 on the back side of page 4, etc. Or, if you prefer, you can write your
corrections on a blank copy of the test.
2. Prepare orally (do not write) §3.2 #25-36 all on pp. 258-259.
3. Write #45-55 all on p. 259. The first one is done for you below as an
example, and you may copy it if you wish.
45. f (x) = x3
Avg. rate of change = 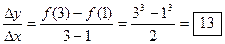
Notice how this work exhibits the “formula, plug-ins, and answer” format that
is typical of most high school math problems. This is a good habit to get
into. Show the steps above for each question. This is not busywork; it is a
way of reinforcing the correct procedures through repeated practice.
|
|
|
W 10/28/15
B
|
HW due:
1. Read §3.3. Reading notes are required, as always.
2. Write §3.2 (pp. 258-262) #81, 89, 90, 93, 94, 99, 100.
3. Write §3.3 (pp. 274-275) #1-12 all.
4. Prepare orally (do not write) §3.3 (p. 277) #51-72 mo3.
|
|
|
Th
10/29/15
C
|
No class. However, Joel, Jack, and Drew should plan
to come in during office hours. There’s no way to get “half-back” correction
points if you haven’t completed your corrections, and the quarter ends
tomorrow. If you have lost your test, then download a fresh copy
and redo the entire test.
|
|
|
F 10/30/15
D
|
End of first quarter.
HW due:
1. Read §3.4 (pp. 279-285). This is only 7 pages, but the reading material is
quite dense. Be sure to work all the “YOUR TURN” segments, and jot answers in
the margin of your book (in pencil). Reading notes are also required, as
always.
2. Make sure that you are up to date on all HW assigned since the beginning
of the year, since a random spot check is possible. All of your HW problems
for the quarter should be stored in your 3-ring binder. Your assignments
should be in order by date and should be easily retrievable on a moment’s
notice. (Some students prefer to keep their reading notes in a spiral
notebook. That is acceptable, but again, the notes for a specified day should
be easily retrievable on a moment’s notice.)
Note for Joel, Jack, and Drew:
Today is the last day that test corrections will be accepted for points.
Don’t miss out on your “half-back” points!
|
|
|
M 11/2/15
E
|
No additional written HW
due.
“Homework amnesty” is now in effect for the first quarter. You may save any
or all of your Q1 assignments if you wish, but they will no longer be
scanned. However, you need to keep all Q2 assignments in your 3-ring binder
until late January, the start of Q3.
|
|
|
T 11/3/15
F
|
No class.
|
|
|
W 11/4/15
G
|
HW due:
1. Write §3.3 (pp. 274-278) #25-47 odd, 49-83 eoo
(every other odd), 85-88 all.
2. Write §3.4 (pp. 286-289) #1-9 odd.
3. Write §3.5 (pp. 299-303) #1-4 all, 5-23 odd.
|
|
|
Th
11/5/15
A
|
HW due:
1. Finish yesterday’s assignment. For repetitious problems where you are sure you understand the concept, you
may use placeholders and shorthand notes to yourself (so that you can present
the problems orally) or short descriptions. For example, if you prefer to
write, “Move graph 2 units to the right, then flip about x-axis, then move entire graph down 3 units,” instead of making a
sketch, then that is acceptable for some of the problems. Make sure you do at
least a few sketches, though, since that is the skill that will be tested.
2. Add the following mixture and “rate of work” problems:
p. 166 #29, p. 167 #31-33
“Allie and Bob.” Allie can paint a
room in 3.2 hours. When she is assisted by her friend Bob, the two of them
working together can paint a room of the same size in 2.7 hours. How long
would Bob take to paint the room if he had to work alone?
“Cal and Doris.” Cal can dig 3
ditches in 2 hours. Doris can dig 7 ditches in 3 hours. If Cal and Doris work
together, how many ditches can they dig in 3.5 hours?
|
|
|
F 11/6/15
|
No school (teacher work
day).
|
|
|
M 11/9/15
B
|
HW due:
1. Read pp. 304-308. Reading notes are required (as always), and an
open-notes quiz on this material is likely. For example, you may be asked
what type of variation is shown by the function 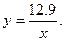
The answer is inverse variation. We
would say that “y varies inversely
with x,” since the form matches the
shaded box on p. 306.
2. Write §3.5 (p. 302) #65, 69, 71, 72.
3. “Edward and Frannie.” Edward
can dig a hole of a certain size in 30 minutes. Frannie can dig a hole of the
same size in 24.5 minutes. How long would it take the two of them to dig that
hole, working together, assuming that their shovels don’t get in the way of
each other?
4. “George and Hermione.” George’s
lemonade is 16% sugar, while Hermione’s is 10% sugar. How many milliliters of
each should be combined to make 250 ml of lemonade with a sugar concentration
of 11.35%?
5. “Ivan and Joan.” Ivan can do a
batch of easy, uniform algebra problems in 25 minutes. When Ivan works
together with his friend Joan, dividing the workload as they go, the entire
batch of problems is finished in 11 minutes. (Note: This is not a permissible way of doing algebra homework. In
Mr. Hansen’s class, you are allowed to check answers with friends, but all
the work shown on your HW paper must be your own work.) How long would it
have taken Joan to solve all the algebra problems if she had worked alone?
|
|
|
T 11/10/15
C
|
No class. However, you will
definitely want to get started early on Wednesday’s homework in preparation
for Thursday’s test.
|
|
|
W 11/11/15
D
|
HW due:
1. Let f (x) be the linear function defined by y = 3x – 7. Let g(x)
= x + 3 be another linear function.
(a) Fred Fumble claims that f and g are inverse functions. As “proof” he claims that if one starts
with the value x = 2 and plugs that
into the f “function machine,” the
result is –1. Then, plugging –1 into the g
“function machine” produces an output of 2. Voila! Right back where we
started! Therefore, g = f –1, i.e., function g is the inverse of function f. Right? Wrong? Prove Fred wrong.
(b) Greg Grimley
claims that Fred Fumble is wrong. Greg offers as “proof” the claim that the
function
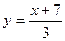 is the real inverse
function of f, since if we start
with x = 2 and plug it is the real inverse
function of f, since if we start
with x = 2 and plug it
into the f “function machine,” the
result is –1. Then, plugging –1 into Greg’s function, we get
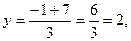 which leaves us
right back where we started. Therefore, Greg claims which leaves us
right back where we started. Therefore, Greg claims
that his function, not Fred’s, is
the true inverse function for f. Is
Greg correct? Explain briefly.
(c) Prove that 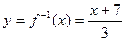 really is the
inverse function of f (x). In other words, really is the
inverse function of f (x). In other words,
prove that for any real number x, f (f
–1(x)) = x, and f –1(f (x)) = x.
(d) State the domain of function f.
(e) State the domain of function f –1.
2. On pp. 317-320, do as many of the odd-numbered review problems, 1-127 odd,
as time permits. Important note: If
you feel that you understand the concept, you may skip to the next group of
questions after getting the hardest one correct. For example, look at
questions 59-64 on p. 318. These are all quite similar, wouldn’t you agree?
Instead of doing 59, 61, and 63, you may decide that #61 is the hardest of the
group and do only that one. However, remember that if you need review on the
concepts involved, you should do all of the review problems in the given
section. Also note: For questions
1-15, 31-41, and 91-99, you may answer the questions orally if you wish.
|
|
|
Th
11/12/15
E
|
Test on Unit 3. There will be a portion with no calculator allowed, as well as a
portion that requires you to use a calculator. Here are some additional
review problems to work on. (Later in the evening, you will receive an e-mail
containing the complete solutions, showing all steps.)
1. Mixture problem. I have 8
liters of a 10% sugar solution. How many liters of 12% sugar solution must I
add to get a solution that is . . .
(a) 11.382% sugar?
(b) 11% sugar?
(c) k% sugar, where 10 < k < 12?
2. “Yancey and Zoe.” Working
together, it takes Yancey and Zoe 58 minutes to mow the lawn. Working alone,
Yancey takes 122 minutes. How long would Zoe take if she worked alone?
3. Let y = f (x) = x3 + x + 1. Let g(x) = 4x – 11.
(a) Plot f on your calculator and
sketch the graph on your paper. Plot the point (1,3), which is a point on the
graph. Show and label all salient points (the point (1,3) and all
intercepts).
(b) Does f appear to be invertible?
Give a reason for your answer.
(c) Prove graphically that g is not
the inverse of f.
(d) Prove algebraically that g is
not the inverse of f.
(e) Name at least 3 points that must be on function f –1.
(f) Sketch function f –1,
using an appropriate dotted line as a guide. (Show the dotted line also.)
(g) Warning: Rated X for extreme
fright. Visit wolframalpha.com and request the inverse of y = x3 + x + 1.
Do you see why sometimes we do not ask students to compute a formula for the
inverse of a function?
(h) Simplify the functions 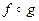 and and 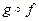 , and compute the value of g(f (–2)). , and compute the value of g(f (–2)).
(i) Is f
even, odd, or neither? Explain briefly.
(j) Function g is neither even nor
odd. However, some linear functions are odd. Give an example.
(k) How many linear functions exist that are even? Explain briefly.
4. Suppose that I have a list of all the ordered pairs that belong to a
relation. Assume that the list has been pruned to avoid redundancy. (For
example, if (1,3) is in the relation, we would list (1,3) only once.)
(a) Complete the sentence: This relation is a function if and only if no x-value __________________ .
(b) Briefly explain your answer to part (a).
(c) Complete the sentence: Assuming the relation passes the condition in part
(a) and is really a function, then the relation is one-to-one if and only if
_____________________________________________ .
(d) Give an example of a non-polynomial function that satisfies the condition
in part (c).
(e) Give an example of a polynomial function of degree 3 or higher that does
not satisfy the condition in part (c).
5. YAMP (Yet Another Mixture Problem).
(a) I wish to combine 5 kg of sand (density 3 times that of water) with 7.8
kg of a lead alloy (density 4.5 times that of water) and an unknown mass of
water to make a sloppy mess whose density is exactly 4 times that of water.
Find the mass of water needed.
(b) If I combine 250 cm3 of water with 750 cm3 of sand,
approximately what volume will the mixture occupy?
6. YASWP (Yet Another Shared Work
Problem). Kevin can build a snow fort of a certain size and quality in 19
minutes and 45 seconds. Laura is twice as efficient as Kevin, and Margaret is
1.5 times as efficient as Laura. If Kevin, Laura, and Margaret work together,
how long will it take them to build the snow fort? (Assume no loss of time
caused by miscommunication, arguments, snowball skirmishes, or interference
with each other.) Give answer in minutes and seconds, rounded to the nearest
second.
After you have worked on review problems, be sure to check all your answers
in the back of the book. Additional
worked solutions and solutions to all the recent problems above are now
available.
Note: The solution to #5(a) has
been revised. Look at the last page of the solutions for a 2-point bonus
opportunity.
|
|
|
F 11/13/15
F
|
No class. However, there is
a 2-point bonus opportunity (see last page of review
solutions) that you can submit by 3:00 p.m. today if you wish.
|
|
|
M 11/16/15
G
|
HW due: Read §4.1 (pp.
326-337). Work through the examples with pencil, paper, and calculator at the
ready. (You don’t have to re-work the examples, but read through the steps
and check them.) Also solve the one problem below.
7. YOMMP (Yet One More Mixture
Problem).
Irv is taking an algebra class in which HW and quizzes are each weighted as
25% of the course grade, tests are 40%, and class participation is 10%. His
quarter averages are 95 for HW, 78 for quizzes, 81 for tests, and “TBD” for
class participation. (The teacher is withholding a determination of the class
participation score until the very end of the quarter.) What score does Irv
need in class participation in order to earn
(a) an A for the quarter (90 or greater)
(b) a B+ for the quarter (85 or greater)
(c) a B for the quarter (80 or greater)
(d) a C+ for the quarter (75 or greater)
|
|
|
T 11/17/15
A
|
HW due: Correct last
Thursday’s test (Form A
or Form B) to 100%. Please
write corrections on a separate sheet of paper. Number each problem so that
the corrections are easy to spot-check at the beginning of class. Kevin, your
test will be scanned and sent to you. (Send e-mail to Mr. Hansen with __Test
Request as the subject line, and your test will be e-mailed back to you.)
|
|
|
W 11/18/15
B
|
HW due: Write §4.1 (pp.
338-342) #1-8 all, 9-30 mo3.
Note: For problems 9, 12, 15, 18,
and 21, use your calculator’s Y1= plotting feature after you have made your sketch,
simply to verify that you did it correctly. For problems 24, 27, and 30,
follow the example established on p. 331. (This is a review of completing the
square.)
|
|
|
Th
11/19/15
C
|
No class.
|
|
|
F 11/20/15
D
|
HW due: Read most of §4.2.
You may omit the Intermediate Value Theorem on p. 348.
In class: Guest speaker, Mr. Joe Morris of MITRE Corporation.
|
|
|
M 11/23/15
E
|
HW due: Write §4.2 #1-18
all, 27-43 odd.
|
|
|
T 11/24/15
F
|
No class.
|
|
|
M 11/30/15
G
|
HW due:
1. Read §4.3. Reading notes are required, as always.
2. Write §4.3 (pp. 364-365) #33-60 mo3. Note:
It is strongly recommended that you use synthetic division throughout.
However, since synthetic division works only if you have a linear divisor,
you will have to be creative when you get to #57.
Also note: You can check all of
your answers, even the even-numbered ones, by using wolframalpha.com.
3. Write §4.3 (pp. 364-365) #66-72 all. These are all suitable quiz or test
problems.
|
|
|
T 12/1/15
A
|
HW due:
1. Read §4.4, including the interesting footnote at the bottom of p. 366 and
the tan box (IVT) on p. 376. However, omit pp. 372-373 and the rest of pp.
375-379. We will not be discussing
Descartes’s rule of signs, the upper and lower bound rules, the bisection
method, Newton’s method, or any of the other advanced techniques for
factoring and graphing polynomials.
2. In the previous paragraph, it was stated that we will not be discussing a
whole group of topics. Why not? Write your answer (one sentence or fragment)
as your first HW answer. (Number this question as #2.)
3. Write §4.4 (pp. 380-381) #1-10 all, 11-19 odd, 73.
|
|
|
W 12/2/15
B
|
HW due:
1. Read §4.5. Reading notes are required, as always.
2. Write §4.5 (pp. 388-389) #1-31 odd, 57-64 all. Note: Exercises 59-64 should all be accompanied by a short
explanation. The first two are done for you below as examples.
59. False in general; true iff x2 – 1 is a factor of the original polynomial.
60. All real zeros of a polynomial
function correspond to x-intercepts.
False as originally stated.
|
|
|
Th
12/3/15
C
|
No class.
|
|
|
F 12/4/15
D
|
Class as usual. However,
Form IV students will not be attending because of House Tour duties.
HW is due for today and is
required. The assignment is the same assignment as in the 12/2 calendar
entry. Completion is expected. Please stop by Thursday after school if you
are having any difficulty completing your work. If you don’t stop by,
completion and correctness are expected when the problems are collected on
Monday.
Update: Nobody stopped by, which means that everyone must have complete
homework when this assignment is collected and/or spot-checked on Monday.
|
|
|
M 12/7/15
E
|
HW due:
1. Read §4.6 (pp. 390-404). Reading notes are required, as always. This is a
long chunk of reading, and you may need to read it twice to get some of the
ideas to settle in your brain. A quiet room and an uninterrupted block of
time are strongly recommended.
2. Be aware that your §4.5 assignment (originally due 12/2, then extended)
may be spot-checked for accuracy and/or collected in its entirety. Nobody stopped
by for help after school last Thursday, nor did anyone stop by during the
last part of the advisory period.
In class: We will begin working the exercises from §4.6, together as a group
and in pairs. Just as in college, you
are expected to have done the reading in advance. Questions will be
answered, of course, and tricky situations will be explained, but you should
not expect to be “spoon-fed” the material that is printed in your textbook.
For example, the definitions of proper and improper rational functions (p.
395) will not be retaught, since it is assumed that you can read those words
for yourself. Your teacher’s job is to clarify the situations in which those
definitions apply and to give you examples to help you work exercises and
progressively more difficult problems related to the material. Your teacher’s
job is not to read definitions out loud to you (nor to write definitions on
the board) in a way that duplicates what is already printed in the textbook.
|
|
|
T 12/8/15
F
|
No class.
|
|
|
W 12/9/15
G
|
HW due: Write §4.6 #1-8
all, 11-19 odd, 27-32 all, 71, 72.
|
|
|
Th
12/10/15
A
|
HW due: Write §4.6 #21-25
odd, 35-55 eoo, 59-62 all, 73-78 all.
|
|
|
F 12/11/15
B
|
HW due:
1. Finish yesterday’s assignment if you have not already done so.
2. Work a selection of the following review problems. Your test next week
will be assembled primarily from problems like these: pp. 414-417 #1-4 all,
5-23 odd, 26-29 all, 31, 33-51 all, 53, 56, 65-69 all, 71-75 all, 77-81 odd,
87-90 all, 95-99 odd (parts b, e, and f only), 109-115 odd, 117-130 all, 139,
140.
Note: You may use your calculator
for all problems except #117-128. For those problems, you need to do them
without your calculator (since that may be required on the test), but you may
use your calculator to check them afterward.
In class: Review.
|
|
|
M 12/14/15
C
|
No class.
|
|
|
T 12/15/15
D
|
HW due: Continue working on
a selection of review problems from those assigned last week. Maintain a time
log, and attempt to finish all of them. Remember, tomorrow’s test will
consist primarily of problems like those review problems.
In class: Review.
|
|
|
W 12/16/15
E
|
Test on Unit 4.
|
|
|
Th
12/17/15
F
|
No class.
|
|
|
F 12/18/15
G
|
Video presentation on chaos
and fractals. If you miss class for any reason, you will be required to view the video on your
own time. There is a technical glitch at 51:30, but when you get there, you
can work around the glitch by waiting a moment and then pressing the left
arrow key or by manually resetting the play point to 51:31. The line that is
partially garbled is this: “Math is our one and only strategy for
understanding the complexity of nature,” spoken by Dr. Ralph Abraham of the
University of California, Santa Cruz.
|
|
|
M 1/4/16
A
|
Classes resume. An
open-notes quiz on the fractals video is likely.
Optional HW: Take a look at this video of a tiny
portion of the Mandelbrot set.
|
|
|
T 1/5/16
B
|
HW due:
1. Complete #140 on p. 417. When you transfer the sketch from your graphing
calculator to your HW paper, use a different color of ink for f and f –1. Note:
Make your sketch fairly large, so that all the details can be seen clearly.
2. Add a dotted line of symmetry to show that your functions really are
mirror images of each other. Label the x-
and y-intercepts of each function.
3. What is the equation of your line of symmetry? Why?
4. Show that each of the following values, when run through the f machine (and then have that result run through the f
–1 machine) will return you to your starting point. Show work.
(a) 17 (a.k.a. Joel’s favorite number)
(b) 27 (a.k.a. Mr. Hansen’s favorite number)
(c) a real number of your own choice (but not an integer) that is in the
domain of f
(d) a general number x (use
algebra, and be sure to state any restrictions on x)
5. Repeat step 4 (parts a, b, c, and d), except this time use the f –1 machine first and the f machine second.
|
|
|
W 1/6/16
C
|
No class.
|
|
|
Th
1/7/16
D
|
HW due: Read through Mr. Findler’s excellent review packet for the midterm exam,
and make some excellent progress on
separate sheets of paper (not directly on the review packet sheets). Keep
a time log. You may omit some of the questions, especially in areas where you
are already skilled. Use standard HW formatting rules, and mark the problems
as 0.1, 0.2, 0.3, 1.1, 1.2, 1.3, etc., in order to indicate the chapter
number and problem number.
|
|
|
F 1/8/16
E
|
Before school, at 7:00 a.m. sharp, there will be a
special retest “by invitation only.” The purpose is to allow students who
failed the Dec. 16 test to have an opportunity to earn a low passing grade.
Invitations will be distributed by e-mail late Wednesday evening.
HW due: Continuation of Thursday’s assignment. A minimum of another 35
minutes of review must be documented.
|
|
|
F 1/15/16
|
Midterm Exam (20% of your semester grade), Trapier Theater, 11:00 a.m. to 1:00 p.m.
If I am still in town during the week of January 11-15, I will be happy to
hold a review session. However, since that is iffy, you should probably try
to see Mr. Findler or Mr. Henry if you have Algebra II questions. (Or, you
can send me an e-mail with a double underscore prefix in the subject line.)
Watch this space for further updates.
|
|
|
W 1/20/16
D
|
Classes resume.
|
|