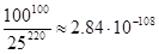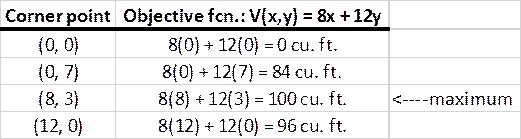|
Schedule
at a Glance (see archives for older entries)
Written assignments should follow the HW guidelines.
|
|
|
W 1/20/16
D
|
Classes resume.
|
|
|
Th
1/21/16
E
|
HW due:
1. If you did not have Mr. Hansen last semester, log in to the e-mail service
you check most frequently, and send Mr. Hansen an e-mail message with the
following subject line:
__Hello from [your name]
Be sure that you put 2 underscore characters before the word “Hello,” exactly
as shown. Be sure to include your name, since it is not always possible to
determine a person’s name from an e-mail address alone. In the body of your
message, please write something that Mr. Hansen should know about you.
2. Write §5.1 (p. 434) #1-25 odd, 27-32 all, 33, 35. Try to follow the HW
guidelines (see link at top of schedule). New students will have their HW
reviewed and critiqued; all others will be expected to follow the same
guidelines from last fall.
|
|
|
F 1/22/16
F
|
Snow day. The assignment
originally due today (Block 2) has been postponed until Monday. If Monday
also turns out to be a snow day, you will need to check this page for
additional assignments that will be due when school resumes.
|
|
|
M 1/25/16
G
|
Snow day. However, the
following assignment is still due today:
1. Read §§5.1 and 5.2 (pp. 422-447). Reading notes are required, as always.
2. Continue to monitor www.modd.net for additional assignments if the snow
break continues beyond the weekend.
|
|
|
T 1/26/16
A
|
Snow day. However, the
following assignment is still due today:
1. Make sure you have completed all the assignments above. The e-mail
requirement (see 1/21 calendar entry above) has not yet been met by Malcolm S.
2. Write §5.1 (p. 435) #49-59 odd, 66-74 all, 81. Yes, word problems with exponential functions are a little
trickier than the word problems you did last semester involving direct
variation, joint variation, and inverse variation. No, exponential models are not much trickier, and no, you do not have to have a special
class period taught by Mr. Hansen in order to figure out how to work with
them. You may copy the solution below for #49 if you wish (no penalty):
49. Given: Pop. doubles every 88
years.
Let x
= # of years elapsed since 2002 (0 means 2002, 1 means 2003, etc.).
Let y
= predicted pop. (millions)
Model: y = f (x) = k · 2x/88
[Reasonableness check: f (0) = k · 20/88 = k
· 20 = k, and f (88) = k · 288/88 = k
· 21 = 2k. Both OK.]
By insp., k = 7.1, since we want f
(0) = 7.1 and f (88) = 14.2.
Want pop. in 2050, i.e., f (48).
f
(48) = k · 248/88
=
7.1 · 248/88
=
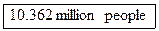
[Note: Clearly, rounding to 1
decimal place to get 10.4 million is appropriate. However, this is not a
science class. To train you for possible AP exams in calculus or statistics
that you may take someday, we will always give answers correct to at least 3
decimal places after the decimal point.]
Do you see how doing a problem like this is almost exactly the same technique that you used last semester
when solving word problems involving direct, joint, and inverse variation?
The only real change is that when writing down a model, you will write down
something like y = k · ax instead of y
= kx or y = k/x.
|
|
|
W 1/27/16
B
|
HW due:
1. Send e-mail to Mr. Hansen for any of the problems due Tuesday that you
were unable to solve. Use the following subject line:
__Section 5.1 Q&A from [your name]
Note that the leading two underscore characters in the subject line are required. Mr. Hansen receives hundreds
of e-mails in a typical day and will never find student e-mails amidst the
chaff unless you use a uniform convention to make your e-mails stand out.
Also, if your e-mail gets routed to the spam bin by mistake, having a uniform
subject line makes it much easier to find among the spam. Putting your name
in the subject line makes it much easier for Mr. Hansen to track threads from
multiple students.
Because you are all 15 or 16 years old and can follow instructions if you put
your mind to it, any e-mails whose subject lines do not conform to the
formatting requirement shown above may be ignored. If you do not receive a
response within a reasonable amount of time and have followed the
instructions for formatting your subject line, you may assume that your e-mail
has been incorrectly identified as spam, and you may leave a message on Mr.
Hansen’s voicemail. (See contact information on modd.net home page.)
2. Write §5.2 (pp. 447-448) #1-63 odd, 65-70 all. The first two in the first
two groups are done for you as examples, and you may copy them. Note that you
cannot simply write the answer, since the setup is part of what you must
write in each case. The symbol “ ” means “implies” and is a substitute for starting a
fresh line. ” means “implies” and is a substitute for starting a
fresh line.
1. log5 125 = 3 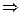 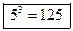
3. log81 3 = 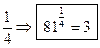
21. 83 = 512 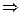 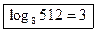
23. 0.00001 = 10–5 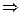 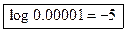 [no need to indicate
base since log means log10] [no need to indicate
base since log means log10]
|
|
|
Th
1/28/16
C
|
No class.
|
|
|
F 1/29/16
D
|
HW due:
1. Read §5.3 (pp. 451-457).
2. Write §5.2 (pp. 448-450) #72-80 eoe (use
calculator to check after you have
made each sketch by hand, with at least 2 points labeled in each case), 83,
89, 92 (OK to use 91 as a hint), 99, 102-108 all.
|
|
|
M 2/1/16
E
|
HW due:
1. Read §5.4 (pp. 460-467).
2. Write §5.3 (p. 458) #3-30 mo3, 45-54 all (OK to use calculator for #45-54,
but please do not use the logBASE function except
as a cross-check). Note: Show work
for those that cannot be solved by inspection. For example, #17 was not
assigned, but here is how you would do it:
17. 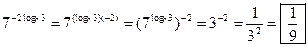
|
|
|
T 2/2/16
F
|
HW due (Block 2 only)
1. Write §5.3 (pp. 458-459) # 55, 56, 59-66 all, 68, 70.
Hint: #68 is rather tricky.
However, if you can’t get #68 to work out, you can still use it as a
corollary to solve #70 in a snap.
|
|
|
W 2/3/16
G
|
HW due (Block 3 only):
See yesterday’s calendar entry.
|
|
|
Th
2/4/16
A
|
HW due:
1. Without using WolframAlpha.com, prove that
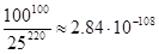 , ,
where the approximation is correct to 3 significant figures. You may use your
calculator and your knowledge of logarithms.
2. Write §5.4 (pp. 467-468) #5-75 mo5.
3. Use the Dep-Scribble-SwykEA
process to solve problems #85-88 all (all on p. 468).
|
|
|
F 2/5/16
B
|
HW due:
1. Finish the assignment that was due yesterday. Note: You cannot use a placeholder for credit today on problems such
as #88, which is easily solved using the 2nd CALC Intersect feature of your
calculator.
2. Write the following additional problems in §5.4 (pp. 469): #91-98 all.
|
|
|
M 2/8/16
C
|
No class.
|
|
|
T 2/9/16
D
|
HW due:
1. Read §5.5 (pp. 470-476). At the beginning of your reading, make the
following changes to your textbook in pencil (or in pen, if you prefer):
(a) For the first 4 standard models on p. 470, make a note in your textbook
that c > 0. These models are
virtually always used for positive quantities (population, density, mass,
etc.), and therefore c > 0
should be stated as a ground rule.
(b) For the second standard model on p. 470, exponential decay, delete the
minus sign and change the note to say that k < 0. In other words, we will make our lives simpler if we
consider only one standard model and let the sign of k determine whether we are modeling growth or decay. The standard
model for all exponential word
problems is y = cekx, and the only
thing we have to remember is that if k
> 0, we have growth, and if k
< 0, we have decay.
(c) For the fifth standard model on p. 470, cross out the function f (x)
= a + c log x. We never need
this, since the common log is simply a constant times the natural log (ln)
and can therefore be absorbed in the constant. Optional extra credit (1 point): Explain why the common log of
any positive number is always simply a constant times the natural log of that
number.
(d) For the fifth standard model on p. 470, change the c in f (x) = a + c ln x to b. In other words, the function should be f (x) = a + b ln x. (The reason
will become clear later on.)
(e) On p. 474, near the top of the page, cross out the solution to part (c).
This is not the correct way to find the predicted number of boys who weigh
between 94.5 and 95.5 pounds. The correct method is taught in AP Statistics
or in any college statistics class, and that will be at least 2 years in the
future for you. As a result, we will use Gaussian models only for sketching
the overall shape of a distribution, not for doing computations of the type
shown in part (c).
2. We have looked at exponential functions of the form y = Bx,
where B denotes a base that must be
positive but not equal to 1. Common values for B are 10, 2, and e. If 0 < B < 1, we have exponential decay, whereas if B > 1, we have exponential growth.
In §5.5, we will enlarge our definition of exponential functions to make them
more flexible to fit more real-world problems. Our new definition, found on
p. 470, is to rewrite all exponential functions in terms of e. As you can see on your marked-up
version of p. 470, all exponential growth problems can be modeled by a
function of type y = cekx,
where c and k are constants chosen to match the requirements of the problem,
with c > 0 and k > 0. Similarly, all exponential
decay problems can be modeled by a function of type y = cekx,
where c and k are suitable constants, with c > 0 and k < 0.
(a) Prove that for any positive real number q and for any real number r,
qr
= er
ln q. Note: This is a quick proof, but if you can’t get it, you are NOT PERMITTED to stop. Instead, you
should accept the fact that qr = er ln q
as a given and move on, since you will need this fact for parts (b) and (c).
(b) Consider the exponential growth equation y = 1.08x,
which models the value of a $1 investment at an 8% compound annual return.
Rewrite this equation in the standard form shown on p. 470 with k > 0.
(c) Show that the exponential decay equation y = 100 · 0.85x,
which models the percentage of unsold and unreplaced
inventory that remains in a store with a 15% annual “shrinkage” problem,
results in 85% remaining after year 1, 72.25% remaining after year 2, and
about 61.4% remaining after year 3. (“Shrinkage” refers to theft, breakage,
rotting, and all other losses except for legitimate sales.)
(d) Consider the exponential decay equation given in part (c). Rewrite this
equation in the standard form shown in your marked-up version of p. 470, with
k < 0.
(e) Let us accept as a given that all exponential growth or decay problems
can be rewritten in the standard form y
= cekx,
as listed on your marked-up version of p. 470. Prove that the inverse
function is always of the form y = a + b ln x, where a and b are constants.
Optional extra credit (1 point):
Prove that in part (d), the inverse function y = a + b ln x always has b < 0
if k < 0, whereas b > 0 if k > 0.
4. Write #7 and #13 on p. 477.
5. Comment briefly on #13. (Hint:
It helps if you paid attention to Mr. Hansen’s chapel talk on Dec. 7, or if
you have seen The Big Short, or if
you paid attention to anything happening during the year 2007.)
|
|
|
W 2/10/16
E
|
HW due:
1. Read the following solution by Mr. Hansen of #25 on p. 478. Then, apply
the same ideas to solve #26, #27, and #28.
25. Let TS = 72 = surrounding temp. (in °F.)
Let T0
= 325 = initial temp. of pie (in °F.), assuming the pie was in the oven for a
long time
Apply Newton’s model: T(t)
= TS + (T0 – TS)e–kt
Plug in to get T(t) = 72 + 253e–kt
SWYK: We know T(10) = 72 + 253e–k(10) = 200
Algebra: 253e–k(10) =
200 – 72
253e–10k = 128
e–10k = 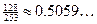 [Note: Three dots indicate additional accuracy stored in calc.] [Note: Three dots indicate additional accuracy stored in calc.]
ln
e–10k = ln(0.5059...)
–10k = ln(0.5059...)
–10k = –0.681...
k = 0.0681...
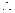 Particular model is T(t) = 72 + 253e–0.0681...t Particular model is T(t) = 72 + 253e–0.0681...t
Plug in t = 30 to get T(30) =
104.763... or 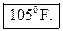 to nearest degree. to nearest degree.
2. Write the following chapter review exercises on pp. 484-487: #9, 11, 13-16
all, 25, 26, 29-40 all, 45-56 all, 68-94 even, 103, 105. Note: There are too many to do all in one night. This assignment
may be continued until Thursday if necessary. Keep a time log.
|
|
|
Th
2/11/16
F
|
HW due (Block 2 only):
Finish the problems assigned for yesterday.
|
|
|
F 2/12/16
|
No school (faculty
professional day).
|
|
|
M 2/15/16
|
No school (holiday).
|
|
|
T 2/16/16
G
|
HW due (Block 3 only):
Finish the problems assigned for last Wednesday.
|
|
|
W 2/17/16
A
|
HW due:
1. Finish any remaining problems from the review set assigned for last
Wednesday, a week ago. Correct answers are expected for all problems, since
you have had more than a week to work on these.
2. Skim §6.1 and §6.2 (pp. 492-520). You are not expected to read every word,
since virtually all of this material should be familiar to you from previous
classes. The only new terms are secant
(the reciprocal of the cosine function), cosecant
(the reciprocal of the sine function), and cotangent (the reciprocal of the tangent function). You are
expected to be familiar with the definitions and abbreviations of the 6
functions listed in the light brown box on p. 511. Reading notes are
required, as always.
Note: Form III students are
permitted to show extremely brief reading notes because of the class field
trip to Ford’s Theatre. We would have had the test today if it had not been for
that field trip.
|
|
|
Th
2/18/16
B
|
Test (100 points) on Chapter 5.
|
|
|
F 2/18/16
C
|
No class.
|
|
|
M 2/22/16
D
|
HW due:
1. Prepare for oral quizzing: §6.1 (p. 504) #1-15 all, §6.2 (p. 520) #13-24
all.
2. Write §6.1 (pp. 504-506) #17-69 eoo (“every other
odd,” i.e., 17, 21, 25, etc.)
3. Write §6.2 (pp. 521-523) #39-50 all, 55-62 all, 91-94 all.
There will be a 7:00 a.m. retest later this week for students who failed last
Thursday’s test. The date will be posted soon.
|
|
|
T 2/23/16
E
|
HW due:
1. Read §6.3 (pp. 524-531).
2. Prepare for a possible open-notes quiz on significant digits. (For
example, 0.04 has 1 significant digit, whereas 38 has 2 and 38.0 has 3.)
3. Prepare for a possible closed-notes quiz on basic calculator functionality
(understanding scientific notation, STOing values
into variables, evaluating functions accurately, plotting in a suitable
window).
|
|
|
W 2/24/16
F
|
Retest on Chapter 5: Required for all students whose
score written on the first page on last week’s test was below 65. The retest will begin in MH-102 at 7:30 a.m. sharp.
(This is a change, since the faculty meeting starts at 8:30 instead of the
usual 8:00.) Please arrive 5 minutes early so that we can start promptly at
7:30.
Note 1: After a review of all
scores for both classes (mean of 60 in Block 2, 68 in Block 3), it seemed
prudent to add a 5-point general curve to everyone’s score. Thus you should
not come at 7:30 if the score written on the first page of your test was 65
or higher. After the adjustment, your score will be 5 points higher than the
score written on the first page of your test.
Note 2: The retest is not intended
for everyone who wants to boost his score, since the classroom is not big
enough to hold everyone who wants to boost his score. The purpose of the retest
is to give people who had major difficulties on the original test a chance to
move into the passing zone, period.
Optional Point-Boosting Opportunity
for all other students will begin at 8:10 a.m. sharp. Please wait quietly in
the hallway until 8:10. At 8:10, the door will fly open, and you will have a
chance to do one or two problems or proofs. If you do well, points will be
added to your test score. If you do poorly, your test score will stay as it
is.
If you cannot attend either event, for
illness or appointment or other reason, please e-mail Mr. Hansen immediately
(with double underscore __ at the beginning of the subject line) to make
alternate arrangements. An alternate “point-boosting opportunity” will be
held in MH-102 during flex time, 11:25-11:45, by invitation only. Most people
who want to boost their score need to show up at 8:10.
Practice tests (blank copies) are available here: Version A (Block 2) Version B (Block 3)
Solution keys are available here: Version A (Block 2) Version B (Block 3)
HW due (Block 2 only): Write §6.3 #1-45 eoo.
|
|
|
Th
2/25/16
G
|
HW due (Block 3 only):
Write §6.3 #1-45 eoo.
|
|
|
F 2/26/16
A
|
HW due:
1. Read §6.4.
2. Be sure that you have completed all the previously assigned problems in
§6.3. (This assignment has been corrected in the previous calendar entries to
#1-45 eoo, not #1-47 eoo,
since #47 does not come up in the sequence.)
3. Prepare for oral presentation: §6.4 (p. 549) #1-17 all.
A special thank-you to Will P., Will A., and Matthew D. for teaching the
first 15 minutes of yesterday’s Block 3 class!
|
|
|
M 2/29/16
B
|
Before school, at 7:10 a.m. sharp: A special
“Re-Retest” will be held, by invitation only, for people who continued to
struggle on last Wednesday’s retest. Send e-mail if you are unsure as to
whether or not you qualify.
HW due:
1. Write §6.4 (pp. 549-551) #73-95 odd, 103-116 all.
2. (Optional, but well worth it.) Watch this
video about a scale model of our solar system. Note: At the same scale used in the video, the next closest
star, other than our sun, would be more than 10,000 miles away.
|
|
|
T 3/1/16
C
|
No class.
|
|
|
W 3/2/16
D
|
HW due:
1. Read §6.5 (pp. 552-564).
2. Write §6.5 (p. 564) #1-10 all. A sketch for each question is required.
|
|
|
Th
3/3/16
E
|
HW due:
1. Write §6.5 (pp. 564-565) #11-24 all, including the ones that we already
did in class.
2. Write §6.5 (pp. 565-567) #47-69 odd, 77, 78, 91, 104.
|
|
|
F 3/4/16
F
|
HW due (Block 2 only):
1. Read §6.6 and §6.7. Reading notes are required, as always. Most, but not
all, of this reading is review of the skills we already learned when building
the Trig Tracker card.
2. Be prepared for a quiz on trig facts. You will be permitted to use your
Trig Tracker card if you wish, but you must work toward performing the skills
without notes in the future.
Sample question: What angle(s)
having nonnegative radian measure less than 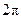 can satisfy the
equation sin can satisfy the
equation sin 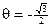 ? Give answer(s) in degrees and radians. ? Give answer(s) in degrees and radians.
Answer: Using our knowledge that 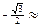 –0.866, we have –0.866, we have 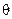 = 240° or = 240° or 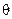 = 300° from our Trig
Tracker card. In radian measure, those angles are = 300° from our Trig
Tracker card. In radian measure, those angles are 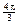 or or 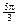 , respectively. , respectively.
Note: If the problem had not
specified the domain restriction for 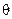 , we would have to consider adding or subtracting all
possible whole-number multiples of 360° from those answers, giving the
following solution set for , we would have to consider adding or subtracting all
possible whole-number multiples of 360° from those answers, giving the
following solution set for 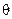 : {240° : {240° 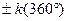 } }  {300° {300° 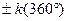 }. In radians, the solution set would be }. In radians, the solution set would be 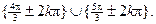 In both solution
sets, the letter k is used to
indicate all possible choices of whole numbers. (Recall that the set of whole
numbers is defined to be the set of nonnegative integers, namely {0, 1, 2, 3,
. . . }.) In both solution
sets, the letter k is used to
indicate all possible choices of whole numbers. (Recall that the set of whole
numbers is defined to be the set of nonnegative integers, namely {0, 1, 2, 3,
. . . }.)
|
|
|
M 3/7/16
G
|
HW due (Block 3 only): See
last Friday’s entry for the other class.
|
|
|
T 3/8/16
A
|
HW due:
1. Write the following review exercises. If you do not finish every last one,
leave placeholders and a time log. We will go over as many as possible in
class. You should be sure to do all the review problems before taking the
test on Wednesday.
p. 652 #5, 9, 13, 16, 18, 19, 25
p. 653 #55, 63, 97-110 all
2. Prepare orally:
p. 652 #35-46 all
p. 653 #67-72 all, 81-96 all
3. Write the following extra problems:
E1. Solve the right triangle having one leg of length 5 m and a hypotenuse of
length 7 m. Give angles in both degrees (nearest thousandth of a degree) and
radians (nearest thousandth).
E2. A car’s camshaft is rotating at 3200 rpm. Compute the angular velocity in
both radians per second and degrees per second.
E3 (Block 3 only, since the fire drill on 3/7 took part of our class period.)
Sketch the tangent function, y =
tan x, where x is in radians. You may use your calculator to help you if
necessary. Show that the domain on which the curve is one-to-one is almost
exactly the same as the domain on which y
= sin x is one-to-one. Use this
fact to sketch the graph of y = arctan x. (Note: The word “arctan”
is simply another name for the inverse tangent function. We say y = arctan x if y is the unique angle strictly between 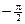 and and 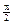 radians whose
tangent equals x.) radians whose
tangent equals x.)
In class: Review.
|
|
|
W 3/9/16
B
|
Test (100 pts.) on §§6.1 through 6.7. Angular
velocity is included, but only the easier types of problems (see, for example
#E2 in yesterday’s review set).
You will be permitted to use your calculator and Trig Tracker card for most
of the test, but a few problems at the beginning will be “no calc, no notes.”
|
|
|
Th
3/10/16
C
|
No class.
|
|
|
F 3/11/16
D
|
HW due:
Read §6.8 (pp. 595-615 and the summary on p. 618 only; skip addition of
ordinates on pp. 615-617). Much of this can be skimmed, since we have already
discussed it. However, you will definitely want to learn the tan box on p.
603, the four bullets at the bottom of p. 607, and the tan box on p. 608.
Reading notes are required, as always.
|
|
|
M 3/14/16
E
|
Pi Day. (Remember, 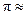 3.1416. Get it?) In
honor of Pi Day and the first warm weekend of the year, there is no
additional HW due today. Hooray! 3.1416. Get it?) In
honor of Pi Day and the first warm weekend of the year, there is no
additional HW due today. Hooray!
|
|
|
T 3/15/16
F
|
HW due (Block 2 only): Not
posted in time because of a technical glitch.
|
|
|
W 3/16/16
G
|
HW due (Block 3 only):
1. Read §6.9. You should read pp. 624-632 (middle) 638). Correct the typo in
the first sentence of p. 626: “increases” should be “decreases.” Reading
notes are required, as always, but you may skim the material from the middle
of p. 632 onward, since it is relatively less important than the earlier
material.
2. Write #41-48 all on pp. 619-620. Do all 8, including the ones that were
done in class. There is no need to show a sketch, but you do need to explain your reasoning. The
first one is done for you as an example:
41. Like sine, but flipped. Period = 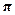 , or 2 times the usual freq. Answer: y = –sin 2x. , or 2 times the usual freq. Answer: y = –sin 2x.
3. Write #97, 98, and 109 on pp. 621-622.
|
|
|
Th
3/17/16
A
|
HW due:
Block 2: Do everything that was assigned for Block 3 (see yesterday’s
calendar entry), plus the following problems from §6.9 (pp. 639-641): #1-8
all, 56-68 all.
Block 3: Finish yesterday’s assignment if you have not already done so. Then,
write the following problems from §6.9 (pp. 639-641): #1-8 all, 56-68 all.
Bonus opportunity for both sections (2 points): Derive the equation 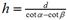 , the parameterized solution
that solves all problems of the type shown in the colorful mountain sketch on
p. 641. The only skills required are algebra and the ability to work with
tangent and cotangent functions. , the parameterized solution
that solves all problems of the type shown in the colorful mountain sketch on
p. 641. The only skills required are algebra and the ability to work with
tangent and cotangent functions.
|
|
|
F 3/18/16
B
|
HW due:
1. Read pp. 663-665, the box in the middle of p. 686, the box at the bottom
of p. 688, the shaded table on p. 695, and pp. 720-729 (only to the middle of
p. 729). That’s all we’ll be looking at in Chapter 7.
2. Write p. 760 #15-25 odd, 29-31 all, 107-111 odd, 119-130 all. Then, close
the book on Chapter 7. You may use your Trig Tracker card to help you.
|
|
|
Spring break
|
|
|
|
M 4/4/16
C
|
No class.
|
|
|
T 4/5/16
D
|
Classes resume. Come to
class with your learning attitude primed for extreme learning excitement in
Q4!
|
|
|
W 4/6/16
E
|
HW due:
1. Read §8.1. Reading notes are required, as always.
2. Write §8.1 (p. 781) #1-6 all, 13.
Note: You do not need to understand
the content of §8.1 (which will be taught today in class) in order to do #13.
All you need is an ability to sketch (a triangle with auxiliary lines) and a
recollection of your basic 30°-60°-90° facts from geometry.
3. Optional bonus (2 pts.): Use
trigonometry to solve #7. This is harder than #13, but again, it does not
require any of the advanced techniques taught in §8.1.
4 (required for everyone). In class yesterday, we saw that log5 x = 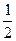 log25 x,
that log9 x = log25 x,
that log9 x = 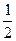 log3 x,
and that log27 x = log3 x,
and that log27 x = 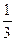 log3 x.
From these and other observations, we came up with a class conjecture: log3 x.
From these and other observations, we came up with a class conjecture:
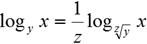
Your assignment:
(a) Be absolutely clear about what the acceptable values (the “givens”) are
for x, y, and z.
(b) Prove or disprove the class conjecture. I will not tell you whether it is
true or false, or whether it is true only for some values and false for
others.
Note: Working with classmates is
acceptable. For this problem (and this problem only), copying a line or two from someone else’s work is
permitted. However, each student must produce a full writeup
written from his own pencil, and the names of collaborators must be
acknowledged.
|
|
|
Th
4/7/16
F
|
HW due (Block 2 only):
1. Read §8.2. Reading notes are required, as always.
2. Write §8.1 (pp. 781-784) #11, 21, 27, 51, 52.
3. In the Tower of Pisa example (p. 780), the fifth substep
of Step 1 says, “Solve for 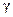 using the inverse
sine function.” However, there are actually two angles between 0 and 180
degrees that have a sine of 0.643619463. using the inverse
sine function.” However, there are actually two angles between 0 and 180
degrees that have a sine of 0.643619463.
(a) Find the other possible angle.
(b) Why did the book completely gloss over the angle you found (or should
have found) in part (a)? Write a complete sentence or two, in your own words.
|
|
|
F 4/8/16
G
|
HW due (Block 3 only):
1. Read §8.2. Reading notes are required, as always.
2. Write §8.1 (pp. 781-784) #11, 21, 27, 51, 52.
3. In the Tower of Pisa example (p. 780), the fifth substep
of Step 1 says, “Solve for 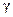 using the inverse
sine function.” However, there are actually two angles between 0 and 180
degrees that have a sine of 0.643619463. using the inverse
sine function.” However, there are actually two angles between 0 and 180
degrees that have a sine of 0.643619463.
(a) Find the other possible angle.
(b) Why did the book completely gloss over the angle you found (or should
have found) in part (a)? Write a complete sentence or two, in your own words.
|
|
|
M 4/11/16
A
|
HW due:
1. Read §8.3 (pp. 796-800). Reading notes are required, as always.
2. Write §8.1 (p. 782) #41, using the Law of Sines. A diagram is also
required.
3. Write §8.2 (pp. 792-795) #17ab (see below), 25, 47, 61, 62.
Note: For #17, solve the problem
two ways:
(a) by using the Law of Cosines
(b) by using a faster method (explain your reasoning).
|
|
|
T 4/12/16
X
|
Diversity Forum (no class).
|
|
|
W 4/13/16
B
|
HW due:
1. Read §8.4 (pp. 804-814). Reading notes are required, as always.
2. On the middle on p. 804, change the word “former” to “latter.” We will use
the notation ||u|| for the
magnitude of vector u, despite
what your book says.
3. On p. 804, change the notation for the vector magnitude from |u| to ||u|| for both occurrences on that page.
4. Near the top of p. 805, change |u|
and |v| to ||u|| and ||v||.
5. On p. 806, change all 7 occurrences of |u| to ||u|| on that
page. Note: Hereafter, whenever we
see the notation |u| being used to
refer to the magnitude (a.k.a. norm) of a vector, we will think of ||u||, but we won’t take the time to
make the change in our textbook.
6. You may wonder how we will indicate boldface type in our written work when
we refer to vectors by their letter names. (No, we won’t bear down harder to
make boldface pencil letters!) The standard used by most mathematicians and
engineers is to put a little arrow over the letter name of the vector, like
this:
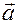
If you prefer, you can make a “shortcut arrow,” like this:
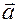
That gives us a way of distinguishing between the variable 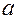 , which is a number, and the vector , which is a number, and the vector 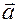 , which is a vector with two components, for example,
<3, –4>. , which is a vector with two components, for example,
<3, –4>.
Your exercise is to prove that for any two vectors, 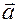 and and 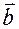 ,
we have ,
we have 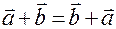 . Be sure to state the “givens” and the “prove” statement
before you begin your proof. Hint:
Without loss of generality, put as the second step in your proof that . Be sure to state the “givens” and the “prove” statement
before you begin your proof. Hint:
Without loss of generality, put as the second step in your proof that 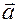 is represented by the coordinates <w, x>
and is represented by the coordinates <w, x>
and 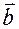 by the coordinates <y, z>. by the coordinates <y, z>.
7. Write the coordinates of the zero vector, namely 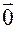 .
Remember to put angle brackets, not regular parentheses, around your answer. .
Remember to put angle brackets, not regular parentheses, around your answer.
8. Your book deals only with vectors in 2 dimensions, but there is nothing to
stop us from having 3, 4, 5, or even 100 or more dimensions. (There are even
infinite-dimensional vector spaces!) Although we will usually stick to 2
dimensions to keep things manageable, write the formula for ||u|| if u is the 3-dimensional vector <3,–4,12>. Show work and
simplify your answer. Hint: Think
back to geometry class. The norm of a 3-dimensional vector is the same as the
diagonal length for a 3-dimensional rectangular solid.
|
|
|
Th
4/14/16
C
|
No class.
|
|
|
F 4/15/16
D
|
HW due:
1. Write §8.3 (pp. 800-801) #1, 7, 13, 19, 25, 40, 43.
2. Write §8.4 (pp. 814-815) #1-5 odd, 17-23 odd, 35-43 odd, 51-55 odd.
3. Write an answer to the Monty Hall
problem. Be prepared to justify your reasoning.
4. Write answer to both versions (A and B) of the Chest of Drawers problems. Be prepared to
justify your reasoning.
|
|
|
M 4/18/16
E
|
HW due:
1. Download and print out this
worksheet. Punching the edges with a 3-hole punch is recommended (so that
you can keep the worksheet in your 3-ring binder), but there will be no point
deduction if you skip that step. If you don’t have a printer, it is
acceptable to write the setups and answers on a regular set of HW sheets.
2. Despite what the instructions say, do not write your name where indicated
on page 1. Instead, write your name in the upper right corner of page 1 (as
you always do), along with the word “due” and the due date:
due
20160418
3. If you get stuck on the Venn diagrams on page 1 or 3, read the material below.
If you still can’t figure out how to fill in the Venn diagrams, phone a
classmate or send e-mail to Mr. Hansen. Be sure to include a double
underscore (looks like this: __ ) at the beginning of your subject line so
that your message is less likely to be rejected as spam.
4. On the final page, there is a typo in question #4(b). Add a vertical bar
(the “given” bar) as shown here:
(b) P(2nd card is a jack | 1st card
is a jack)
5.
For question #4(c), note that we already solved the problem in class, both by
a priori analysis and with a
computer simulation. You should certainly be able to answer this one
correctly!
6. In question #4(e), if you are not a card player, you may not know what the
phrase “two of a kind” means. The question is asking for the probability that
you obtain two cards of the same value (for example, ace of clubs and ace of
spades, or 10 of diamonds and 10 of spades). One way to analyze this problem
is to imagine that the first card has been chosen, whatever it happens to be,
and you have to draw as your second card one of the other 3 cards of that
same value from the remaining cards. Better yet, run a simulation!
7. You have probably seen Venn diagrams in previous classes, but if not, here
is a filled-in Venn diagram that you can use to get started on your
assignment:

The letter U denotes the universe
of all 50 students. Circles denote the subsets of students who play baseball
and basketball, respectively. Note that 29 (a total of 19+10) students play
baseball, while 16 (a total of 6+10) play basketball, as required. The
diagram also shows 10 students in the intersection region, namely (baseball 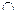 basketball).
Finally, since the problem told us that there are 50 students, we have to
stick the leftover 15 students in a portion of the diagram that is outside
both the baseball and the basketball regions. In other words, there must be
15 students who play neither baseball nor basketball. basketball).
Finally, since the problem told us that there are 50 students, we have to
stick the leftover 15 students in a portion of the diagram that is outside
both the baseball and the basketball regions. In other words, there must be
15 students who play neither baseball nor basketball.
8. (Optional.) The challenge problem is optional but is strongly recommended
for those who have spoken to Mr. Hansen about possibly jumping to the honors
track next year. For the challenge problem, assume that the value of an ace
is 11. The 10, jack, queen, and king all have a value of 10.
|
|
|
T 4/19/16
F
|
HW due (Block 2 only):
1. Read §12.6 (pp. 1167-1174), especially the calculator “Technology Tips” in
the margins of pp. 1172-1173. Reading notes are required, as always.
Note: There is a typo in the
Technology Tip in the margin of p. 1171. The first “6” under the section
marked “Graphing calculators:” should be 13, not 6.
2. Write answers to the following questions. Use your calculator. Your “work”
should consist of your setup, using standard notation. The first one is done
for you as an example. For problems involving combinations, please show both
the “nCr” format and the
“parentheses” format for combinations, since as shown at the top of p. 1172,
the notations are equivalent. You should be equally comfortable with both
formats, though, since both are in common use.
(a) How many 13-card bridge hands are possible?
Solution: 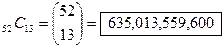
(b) How many 5-card hands are possible in draw poker, with no jokers?
(c) How many Virginia license plates of the form XXX #### are possible?
(Here, “X” denotes a letter, and “#” denotes a digit, 0-9.)
(d) How many 3-student student council delegations (with all ranks considered
equal) can be chosen from a Form IV class of 79 students?
(e) How many 5-student student council delegations (with distinguishable
ranks of Head Prefect, President, Vice President, Prefect 4, and Prefect 5)
can be chosen from a Form V class of 80 students?
(f) How many 5-digit student IDs are possible if the first digit must be a 2
or a 3, and if the remaining digits are allowed to be any digit, 0-9?
(g) How many Internet addresses are possible if an address consists of 4
integers, separated by dots? (For example, 172.8.15.255 is an Internet
address.) Each of the 4 integers must be between 0 and 255, inclusive.
(h) How many different ways can a hamburger be assembled if each burger may
include (or not include) any or all of the following toppings: ketchup,
mustard, lettuce, tomato, grilled onion, raw onion, mayonnaise, grilled
mushrooms, cheese, jalapenos? Note:
All burgers must include a bun and a beef patty. Those are the only required
elements. All of the toppings are optional. The order in which toppings are
applied does not matter. For example, lettuce with tomato and then ketchup
applied over the top of the tomato is considered equivalent to ketchup
directly on the patty and lettuce and tomato piled on top.
(i) If the only possible Republican presidential
candidates for 2016 are Trump, Cruz, and Kasich, and if the only possible
Democratic presidential candidates for 2016 are Clinton and Sanders, how many
different 2-way contests are possible?
|
|
|
W 4/20/16
G
|
HW due (Block 3 only):
See yesterday’s calendar entry.
|
|
|
Th
4/21/16
A
|
HW due:
1. Write §12.6 (pp. 1174-1175) #19, 27, 41-46 all.
2. Write §12.7 (pp. 1184-1185) #27abc, 33, 39, 43, 44-46 all, 59. Note: For #59, interpret “birthday” to
mean month and day of birth, and treat all 365 days as being equally likely.
This is not true in the real world, where August and September are more
popular.
3. Read the Excelcise and practice going through the steps. You
will eventually have to execute all the steps in 5 minutes, and to do that,
your skills will need to be sharp. Note:
Not all instructions are shown on the sheet. You are expected to know certain
standard tricks, such as Shift+arrow key for
selecting cells and Ctrl+B for bold.
|
|
|
F 4/22/16
B
|
HW due:
1. Read this handout. As you
come across unfamiliar terms, read the material below.
Interpolation is one way of
estimating a y-value on a graph. If
you want to estimate the y-value
corresponding to a certain x-value,
you can use x-values to the left
and right (and their corresponding y-values)
to pick a y-value that seems to
make sense. For example, if the temperature at 6 p.m. is 62 degrees, and the
temperature at 9 p.m. is 57 degrees, we can estimate the temperature at 7
p.m. as being about 60 degrees. Here, “time” is playing the role of x, and “temperature” is playing the
role of y. Note that our estimate
for the temperature at 7 p.m. is closer to 62 than to 57, because 7 p.m. is
closer to 6 p.m. than to 9 p.m. If you wanted to
make a linear equation and come up with a more exact estimate, you would look
at the change in temperature (namely, –5 degrees) and allocate that on a
per-hour basis to be 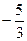 degrees per hour.
The number degrees per hour.
The number 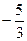 is actually the
slope of the line that interpolates between the points (6, 62) and (9, 57).
The “exact” linear estimate for 7 p.m. would therefore be is actually the
slope of the line that interpolates between the points (6, 62) and (9, 57).
The “exact” linear estimate for 7 p.m. would therefore be 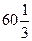 degrees. degrees.
Note: Linear interpolation is valid
only for situations where the change is approximately linear.
Extrapolation is another way of
estimating a y-value on a graph. If
you want to estimate the y-value
corresponding to a certain x-value
that lies outside the domain of data that you have, you can use the trend
line already established and “continue to the trend” to make your estimate.
For example, if the temperature at 6 p.m. is 62 degrees, and the temperature
at 9 p.m. is 57 degrees, what will the temperature be at midnight? If the
trend continues (i.e., dropping 5 degrees per every 3 hours), the answer is
52 degrees.
Note: Linear extrapolation is valid
only for situations where the change is approximately linear and you can reasonably expect that a
trend will continue. If the trend cannot be relied upon, or if the x value you are using makes no sense
in the context of the problem, don’t extrapolate!
Here is an example of extrapolation that makes no sense. When Mr. Hansen was
10 years old, he weighed about 90 pounds. When he was 50 years old, he
weighed about 180 pounds. If the trend continues, what will Mr. Hansen weigh
at age 90?
The “answer” by linear extrapolation is 270 pounds. Clearly, this makes no
sense, since Mr. Hansen may not live to age 90, and it’s especially unlikely
to happen if he weighs 270 pounds.
The “answer” by geometric extrapolation (i.e., doubling weight every 40
years) is even more ridiculous: 360 pounds!
A scatter plot (also called scatterplot) is a graph of x-values versus y-values. You place a dot for each ordered pair that associates
an x-value with a y-value. For example, a scatterplot of
the temperature data given above would require you to plot points at (6, 62)
and (9, 57). That’s all it is. A scatterplot allows us to understand the
trend (if any) in an immediate, visual way. A scatterplot is much better than
a data table for most purposes.
The line of best fit is a line that
minimizes some of the errors that inevitably occur when we use a straight
line in trying to model bumpy, real-world data. You can estimate the line of
best fit by sketching it on a scatterplot, but a better way is to enter the x-values into list L1 on
your calculator (keystrokes: STAT EDIT to display L1, up and down
arrow to enter values into cells) and to enter the y-values into list L2 (same basic technique). Then,
you must press 2nd QUIT to return to the main calculator screen. Finally,
press STAT CALC 8 L1,L2 ENTER. (Note that you must use
the comma key to separate L1 and L2. You enter the
names L1 and L2 by using the 2nd function of the
numbers 1 and 2 on your calculator keypad.)
Note: If you have one of the newer
calculators that uses fill-in screens for all the complicated operations,
such as STAT CALC 8, you should simply press STAT CALC 8 and then tell your
calculator that you want to use L1 for your x-values (“Xlist”) and L2
for your y-values (“Ylist”). Leave “FreqList” and
“Store RegEQ” blank. Highlight the word “Calculate”
and press ENTER to calculate the line of best fit.
Your calculator tells you the line of best fit in a cryptic way: a indicates the y-intercept, and b
indicates the slope. So, you have a line, y
= a + bx, which you can graph on your
calculator as well as on your paper.
2. After you have read the handout
and the explanatory paragraphs above, try to complete the handout. You will
definitely get stuck. This is normal. Do the best you can, and we will
complete the handout in class. Please write a list of specific questions in
the margins of your handout or on the reverse side.
3. Continue practicing for the Excelcise.
We will conduct our first timed trials during class on Friday. Some people
may even pass on the first round!
|
|
|
M 4/25/16
|
No school (Phi Beta Kappa
Day).
|
|
|
T 4/26/16
C
|
No class.
|
|
|
W 4/27/16
D
|
HW due:
1. Continue practicing for the Excelcise.
2. Correct your scatterplot handout
(the one you did for last Friday’s class) to 100% perfection by using this solution key. For full
credit, please follow these guidelines:
(a) Use a different color of ink for your corrections.
(b) Write kind but detailed notes to yourself in the margins, addressing yourself
by name.
BAD EXAMPLE: “Fred, don’t be such
a knucklehead!”
SLIGHTLY BETTER EXAMPLE: “Fred,
don’t be such a knucklehead! Slope is always the value that is being
multiplied by x.”
GOOD EXAMPLE: “Fred, remember that
in the a + bx function that STAT CALC 8
produces, a is the intercept and b is the slope. The slope is always
the value that is being multiplied by x.”
|
|
|
Th
4/28/16
E
|
HW due:
1. Continue practicing for the Excelcise.
A timed trial will be held in class.
2. Complete this worksheet.
In #4, you may omit the box plot if you wish. You can answer everything else,
however. Feel free to use your calculator or Excel to compute the median, the
quartiles, the standard deviation, and so on.
|
|
|
F 4/29/16
F
|
HW due (Block 2 only):
1. Read §9.1 (pp. 876-888). Reading notes are required, as always.
2. If you have not already done so, finish the descriptive statistics worksheet
that was previously assigned. In particular, make sure in #4 to draw the box
plot requested and to compute the interquartile range (IQR). IQR is defined
to be Q3 – Q1, i.e., the value at the 75th percentile minus the value at the
25th percentile.
In #5b and #6a, note that range
(just regular range, not interquartile range) has a different definition in
statistics. The definition is max – min, i.e., the largest value in the data
set minus the smallest value. You should compute answers for #5b and #6a if
you have not already done so. Also note that the definition of the word range in statistics is different from
the definition you learned last fall. In statistics, range is a number . . . not an interval or a set
of values, the way we would use the word range
when talking about the domain and range of a function.
You are encouraged to use your calculator to assist you in sketching the box
plot. (Use your calculator to display the box plot, and then transcribe a
reasonable copy to your HW paper.) Your calculator automatically scales the
box plot correctly if you use 2nd STATPLOT and ZOOM 9.
3. Complete this
worksheet on lines of best fit and their slopes.
|
|
|
M 5/2/16
G
|
HW due (Block 3 only):
See calendar entry for 4/29.
|
|
|
T 5/3/16
A
|
HW due: Review problems. Do
as many of the problems listed below as you can. Keep a time log. For any that
you do not finish, be sure to work them before the test on Wednesday as part
of your study and preparation.
1. Chapter 8 review (pp. 869-870): #1-19 odd, 23, 27, 41, 45, 51, 53, 59, 60,
67, 68.
Probability review:
2. Three fair coins are flipped. Compute
(a) the probability of three heads
(b) the probability of at least one head
(c) the probability of obtaining head, head, tail (in that exact order).
3. Five cards are drawn from a well-shuffled deck (without replacement).
Compute
(a) the probability that
all of them are face cards (J, Q, or K)
(b) the probability of at
least one face card
(c) the probability of at least one ace.
4. Assume that the probability of mumps is 0.1, the probability of chicken
pox is 0.2, and the probability of both diseases is 0.05.
(a) Are the events of mumps and chicken pox independent? How can you tell?
(b) Compute the probability of having neither disease. Make a Venn diagram to
help you.
(c) Compute the probability of having at least one of the two diseases.
(d) Give the correct notation (using union or intersection symbols) for the
probability requested in (c).
Statistics review:
5. Bamboo grows incredibly fast. Some species can grow several feet per day.
Here is a dataset of x-values
(elapsed time in days) versus y-values
(height of bamboo stalk in inches).

(a) Compute the mean, mode, median, and standard deviation of the bamboo
height measurements. Use the following notation to label your answers:
sample mean = 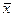 = ____________ = ____________
mode = ____________
median = Q2 = ____________
sample s.d. = s
= ____________
(b) Compute the 5-number summary of the height measurements, and make a
modified boxplot.
(c) Find the line of best fit (linear regression line), and give its
equation.
(d) Use the line of best fit to estimate the bamboo height at 6 days and at
15 days.
(e) Which estimate in part (d) do you trust more, and why? Use the terms interpolation and extrapolation in your answer.
(f) Make a scatterplot with the line of best fit overlaid. Be sure to label
your axes appropriately.
(g) State the slope of the line of best fit. What are its units?
(h) Interpret your answer to part (g) in context. (Note: This is an essential
PSAT/SAT skill.)
In class: Review. Here is a solution
key to many of the review problems.
|
|
|
W 5/4/16
B
|
Test (100 pts.) on 3 of the following 4 topic areas:
Trig, Vectors, Probability, and Statistics.
The fourth topic area will be given to you as a take-home worksheet.
To help you in your study: solution
key to many of the review problems.
Important ROOM CHANGE announcement:
Because our regular classroom will be unavailable today (on account of a
Japanese AP exam), your test will be held in a different location. The Block 2 test will be
held in MH-314. The Block 3 test will be held in LJ-302 (the room at the top
of the stairway found at the extreme end of the Red Hallway of the
Lane-Johnston Building).
|
|
|
Th
5/5/16
C
|
No class.
|
|
|
F 5/6/16
D
|
HW due: Your take-home
portion of Wednesday’s test was e-mailed to you on Thursday morning and is
due at the start of class today. Click here
for instructions.
|
|
|
M 5/9/16
E
|
HW due:
1. Read §9.2 (pp. 893-900). Reading notes are required, as always.
2. Write #5 and #31 on p. 901. Do both problems by hand, using the
adding-and-subtracting techniques illustrated in class last Friday.
3. Use your calculator (see instructions in margins of pp. 894-897, or watch this 4-minute video)
to solve #8 and #12. No need to show any work; simply write your answer as a
set of ordered triples, using the format {(##, ##, ##)}. For example, if your
solution is x = 2, y = –14, and z = 3, you would write
{(2, –14, 3)}
as your answer, since that is a set of ordered triples.
|
|
|
T 5/10/16
F
|
HW due (Block 2 only):
1. Read §9.5 (pp. 928-933). Reading notes are required, as always.
2. Write §9.2 (pp. 901-904) #8-32 eoe, 37, 38, 47,
48, 52. Use your calculator’s rref feature to do
all the heavy lifting, but do show
all your setup work, especially the process of obtaining the linear system
for #32, 37, 38, and 52. “I don’t know” and placeholders will not be accepted
as adequate for #32, 37, 38, and 52. At a minimum, you must send an e-mail
describing the nature of your confusion, speak with a classmate, or consult
some of the example problems earlier in the section.
|
|
|
W 5/11/16
G
|
Field Trip.
Depart STA (bus on service road near Martin Gym) shortly after 8:00 a.m.
Regular school dress is required. We will be back by 1:00 p.m., in time for
lunch and your regular Block 6 class period.
Any Block 3 student who does not go on this field trip should report to
MH-211 (the STAySmart Center, Mr. Findler’s room) at the usual time for roll call and an
assignment that you will work on in the library. Your assignment is to write
the inequalities that produced each of these graphs, and
then begin working on the
rest of tomorrow’s assignment.
HW due (will be collected tomorrow from Block 3): See calendar entry for
5/10.
|
|
|
Th
5/12/16
A
|
HW due:
1. Write the inequalities that produced each of these graphs,
2. Write problems 1, 2, 3, and 4 from this
worksheet. Note that #1 and #3 have already been largely done for you;
try to do the problems on your own, but if you get stuck, you can refer to
the hints at the end for help. A writeup is
required for all 4 problems. Important:
Your writeup must include a list (or table) of
corner points and the objective function value for each corner point; those
are not provided in the hints at the end of the worksheet.
Inequality sketches should be neat (no scribbling) but are not required to be
on graph paper. The purpose of the diagrams is to help you find the corner
points so that you can check each corner point in the objective function to
find the maximum (or minimum).
You are allowed to use desmos.com/calculator
to double-check your graphs. Remember, though, that on the final exam, you
will be required to do all work either by hand or with your graphing
calculator.
3. Finally, remember that if you are in Block 3, there was an additional
assignment that was due yesterday. (See the calendar entry for 5/10.)
|
|
|
F 5/13/16
B
|
HW due:
1. Finish the inequalities
worksheet and the linear
programming worksheet that were due yesterday. Make sure that for each
linear programming problem, you include a table similar to the following
example for #1:
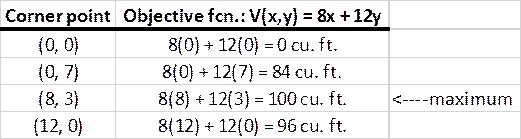
As shown in the example above, please use an arrow to mark the maximum (or
minimum, depending on the problem).
2. Answer this question: Why does it suffice to check only the corner points
of the feasible region? After all, the feasible region in problem #1 (as in
most linear programming problems) includes infinitely many points. Why are we
able to get away with checking only the corner points? A few complete
sentences are expected.
3. Also answer this question: What if the corner point having maximum value
of the volume objective function in #1 had had coordinates of (8, 2.7)
instead of (8, 3)? Would you still accept (8, 2.7) as the solution for (x, y),
or would you require your solution to have both x and y be integers?
Note: Optimization problems in
which one or more of the variables are required to be integers are called integer programming problems. If the
objectives and constraints are all linear, but one or more of the variables
are required to be integers, the problem is called an integer linear programming or ILP problem. We will not study ILP
or integer programming in general, because those topics are too advanced for
Algebra II. However, as you might imagine, ILP and integer programming have
many real-world applications. (Think: airline scheduling, concert tour
scheduling, contingency staffing, emergency response planning, traffic light
timing, urban design, warfighting, political science, marketing, etc., etc.)
|
|
|
M 5/16/16
C
|
Field Trip (alternate date). Depart STA (bus on service road near Martin Gym) at
8:00 a.m. Regular school dress is required. We will be back by 1:00 p.m., in
time for lunch and your regular Block 1 class.
|
|
|
T 5/17/16
D
|
Quiz (40 pts.) on Inequalities, Linear Systems, and
Linear Programming.
You will use your calculator for most of the questions. However, there will
be a few questions in which you are required to do something without your
calculator. For example, you may be required to solve a system of 2 equations
in 2 unknowns by hand, or you may be required to graph the solution set of a
system of inequalities. All linear programming questions will be done with
calculator.
|
|
|
W 5/18/16
E
|
No additional HW due today.
In class: Review, followed by the Scale Model of the Solar System!
|
|
|
Th
5/19/16
F
|
HW due (Block 2 only):
1. Write p. 943 #1-25 all. Calculator is permitted for questions 12, 13, 14,
21, 22, and 24 ONLY. All other questions are to be done without calculator
(except possibly to check your answers).
2. Note: Some of these problems have
already been done in class. That does not matter; write them up neatly on
your HW paper. At least you should be able to get those ones correct!
3. For a few of the questions, which are from the precalculus
curriculum, exercise your metaknowledge and simply
write, “PRECAL.” Do not solve these problems.
4. Keep a time log. Your homework will be graded, not merely spot-checked.
In class: Review.
|
|
|
F 5/20/16
G
|
End of Q4. All bonus points (crossword puzzles,
etc.) must be submitted by 3:00 p.m. today.
HW due (Block 3 only): See calendar entry for 5/19.
In class: Review.
|
|
|
T 5/24/16
|
Final Exam, 2:00–4:00 p.m., Trapier
Theater.
Mr. Hansen’s office hours for exam week are Monday 10:00-2:00, Tuesday
10:00-1:45, and Thursday 10:00-2:00. If you can’t finish your Excelcise and/or Must-Pass Quiz during those times, you
need to contact Mr. Hansen ASAP!
Resources
To assist you, here are some resources you may find helpful:
·
May 4 test on vectors,
trig, probability, and statistics: Blank (Block 2)
·
May 4 test on vectors,
trig, probability, and statistics: Key (Block 2)
·
May 4 test on vectors,
trig, probability, and statistics: Blank (Block 3)
·
May 4 test on vectors,
trig, probability, and statistics: Key (Block 3)
·
May 17 quiz on inequalities,
linear systems, and linear programming: Blank (form A)
·
May 17 quiz on inequalities,
linear systems, and linear programming: Blank (form B)
·
May 17 quiz on inequalities,
linear systems, and linear programming: Blank (form C)
·
May 17 quiz on
inequalities, linear systems, and linear programming: Key (form C)
·
May 17 quiz on inequalities,
linear systems, and linear programming: Blank (form D)
Study Guide
In addition to the cumulative sample test on p. 943, you will want to make
sure you have covered the following areas/topics in your exam review:
·
Probability
(including permutations, combinations, counting rules, Venn diagrams,
multiplication rule, general union rule, general intersection rule, and
conditional probability)
·
Statistics
(including mean, mode, median, standard deviation, scatterplots, boxplots,
and interpretation of the slope of the line of best fit)
·
Linear
programming (including definition of variables/“Let” statement, plotting of
the feasible region, and evaluation of the objective function at each corner
point)
·
Rules of
logarithms (including LPSL, “house rule,” and LQDL rules:
log ab = log a + log b, log xa =
a log x, and log of a quotient equals difference of logs)
·
Solution of
exponential and logarithmic equations
·
Solution and application
of trigonometric equations
·
Conversion
between radian and degree measure (for example, 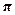 radians = 180°) radians = 180°)
·
Plotting of
trigonometric functions (for example, why does y = 3 sin 2x have a
period of only 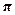 ,
when a typical sinusoid has a period of 2 ,
when a typical sinusoid has a period of 2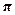 ?) ?)
·
Hero’s Formula,
law of sines, law of cosines, area of triangle by trigonometry (finding
altitude by using a sine function as multiplier)
·
Basic knowledge
from semester 1 (including rules of exponents, simplification of expressions,
quadratic formula, factoring, inverse functions, and domain and range of
functions)
|
|
|
F 5/27/16
|
Update!
There will be additional office hours on Friday, May 27, from 7:30 a.m. to
12:30 p.m. The following people need to be sure to stop by during that window
in order to pass the Excelcise:
Collin
Drew
Joel
Julian
Michael
|
|