|
1.
|
(a) Like all statistics, this sample proportion is a
number computed from data. However, the long-run relative frequency of heads
in the infinite collection of possible coin flips cannot be computed,
although we can estimate the value of that parameter.
(b) a parameter
|
|
9.
|
(a) 0.5, 1.1, 2, 2.5, 2.5
71, 76, 81, 87.5, 93
(b) 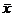 = 1.77 hrs./night [1.8
is acceptable; units are desirable, but no penalty if omitted here] = 1.77 hrs./night [1.8
is acceptable; units are desirable, but no penalty if omitted here]
(c) s = 6.6 dB [units may be
omitted here without penalty]
(d) [checked in class]
(e) The center (median) is about 81 dB. The data show right skewness, with no notable gaps or outliers. The IQR is
about 11.5 dB, and the range is 22 dB. Since the IQR is small relative to the
median, we can say that the data are fairly compressed. [Less thorough
answers that clearly speak to center, shape, and spread of the distribution
are also acceptable. Also, be aware that a 22 dB range, while not excessively
large in terms of human hearing perception, represents a factor of about 150
in terms of power levels.]
(f) [Almost everyone got all the points here. The x-axis must be marked with at least 2 numeric values and the
caption “HW (hrs./night).” The y-axis
must be marked with at least 2 numeric values and the caption “Whininess (dB).”
Note: The y-axis caption should read from bottom to top. However, there is
no penalty if you oriented it from top to bottom.]
(g) negative
(h) Larger values of HW are associated with generally smaller values of
whininess, and vice versa. [Note:
There is a point penalty if you wrote anything about larger values of HW
“causing” generally smaller values of whininess.]
(i) 90 dB [any answer in the upper 80s is also
acceptable]
(j) Insufficient information [not an experiment]
(k) Insufficient information [not an experiment]
(l) Yes
(m) Yes [simply read value on the y-axis
and follow to x-axis value below]
(n) 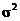 ; dB2 ; dB2
(o) n = 17; convenience sample
Number the students from 1 to 269, write each number on a uniform slip of
paper, mix the numbers up, and draw the desired number of slips from a hat.
Alternate method: Number the
students from 1 to 269, associate each number from 1 to 269 with a
pseudorandom real number (generated by TI-83/84 or by Excel), and use the
column of pseudorandom values as a sort key to reorder the list of 269
integers. Then, choose the desired number of students as the first n values in the newly sorted list.
This method provides an SRS.
|