|
M 3/2/15
A
|
HW due (both
blocks):
1. Read pp. 619-626. Reading notes are required, as always.
2. Write #11.46 on pp. 626-627. Full PHA(S)TPC procedures are required (S
optional).
3. For problems #11.61-11.90 on pp. 634-641, do not solve the problems. Instead, write for each problem a
statement of what type of test procedure is appropriate. Usage of a tabular
presentation and/or ditto marks is permitted in order to reduce busywork. (For
example, a table with columns labeled by test procedure and cells that
contain either a checkmark or no checkmark would be completely adequate.) To
get you started, the first set of answers is provided below:
#11.61(a) 2-sample t test
(b) ditto
(c) ditto
4. What is the purpose of the table you made in the previous exercise? Write
a sentence or two.
|
|
|
T 3/3/15
B
|
Block 3 HW due:
Read the BASP
editorial banning P-values and
confidence intervals, as well as the American Statistical Association’s preliminary response. Optional reading: “Why
Most Published Research Findings Are False.”
In class: Review for test.
Block 4: No class.
|
|
|
W 3/4/15
C
|
Block 3: No
class.
Block 4: Review for test. If you have not already read the articles whose
links are provided in yesterday’s calendar entry for the other section, you
are expected to do so. The third article is optional.
|
|
|
|
Original Test Announcement:
Test (100 pts.) on all recent material. Some older material, dating back to the beginning of the
year, will also be included. However, the only older material that will be
included on this test will be AP-type content. Therefore, you can use your
Barron’s review book (any questions except for 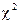 and LSRL t-test) in order to prepare for the
test. and LSRL t-test) in order to prepare for the
test.
Among the older terms that you definitely need to know are the following:
Type I and Type II errors, standard error, confidence interval, confidence
level, test statistic, P-value.
As always, you will be provided with a standard AP formula sheet during the
test. As you probably know, there is virtually no benefit in memorizing
formulas. What you need to know—cold—is what the formulas mean and when to use them.
Assumptions, however, do need to be
memorized:
1-sample t: SRS, normal population
2-sample t: two independent SRS’s,
two normal populations
Paired t test: SRS, normal
population of differences
1-proportion z: SRS, N 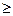 10n, np 10n, np
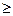 10, nq 10, nq 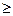 10 10
2-proportion z: 2 independent
SRS’s, N1 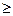 10n1, N2 10n1, N2 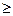 10n2, n1p1 10n2, n1p1
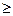 10, n1q1 10, n1q1 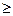 10, n2p2 10, n2p2 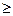 10, n2q2 10, n2q2 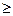 10 10
Note: The assumption of normality
in the t tests can be relaxed if
(1) we can rule out extreme skewness or outliers,
and (2) the sample is “large” (rule of thumb: n 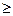 about 30). In the
2-sample t test, we can count both
sample sizes toward meeting the rule of thumb. about 30). In the
2-sample t test, we can count both
sample sizes toward meeting the rule of thumb.
Rules for df:
1-sample t: df
= n – 1
2-sample t: df
= (horrible mess; use calculator)
Paired t test: df
= number of differences – 1
|
|
|
Th
3/5/15
D
|
Snow day for
both blocks.
Test Instructions: Your
“do-at-home” mini-project is here.
Deadline is 3:00 p.m. Friday. (If school is canceled Friday, the deadline
will be extended until 3:00 p.m. on Monday.) The rest of the points on the
test will come from a 20-minute in-class quiz on Tuesday.
|
|
|
F 3/6/15
E
|
Another snow
day.
This is a genuine snow day: a day off with nothing to do. We all know how
depressing that can be. If, instead of vegetating all day, you would like to
spend 65 minutes working on AP review problems, it will be worth your while.
(It’s a fair trade; you would have been in class for 65 minutes today anyway
if the white stuff hadn’t fallen from the sky.) Simply keep a written log of
all your problems, in the place where you keep all your AP review work. Keep
a date and time log, and show your work in class on Tuesday for a few bonus
points.
|
|
|
M 3/9/15
F
|
No class. However,
your “do-at-home” mini-project is due by 3:00 p.m., which is an extension
from the original Friday due date. Submit your papers in person in MH-102.
|
|
|
T 3/10/15
G
|
In-Class Quiz (both blocks),
approximately 50 points.
This will consist of the remaining points from last week’s test.
|
|
|
W 3/11/15
A
|
HW due (both
blocks): Read pp. 629-632, 647-656. If you did not give an oral presentation
yesterday, be prepared to do that also.
|
|
|
Th
3/12/15
B
|
HW due (Block
3):
1. Read pp. 660-671, 677-680, and the summary of key concepts and formulas on
p. 681.
2. Perform Activity 12.1, working alone. If you did not start this activity
before leaving school on Wednesday, you may ask 5 people 5 digits each, since
it would be difficult for you to find 25 people. Surely you can find 5
people, even if you have a small household. Use the Internet if necessary. In
#5 (carrying out the hypothesis test), be sure to show all your work. You may
adapt the following table for your purposes. (Your raw data and category/bin
counts will be different, of course.) Test at the 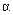 = 0.05 level. = 0.05 level.

3. Think about: An interesting question was posed in Block 3 on Wednesday,
3/11. The t* value for a 99%
confidence interval is much larger than the t* value for a 98% confidence level. How can this be? (For df = 1, the difference is a whopping factor of 2. However,
even for df = 10, the difference is still large,
with the 99% value being almost 15% larger than the 98% value. The difference
between t* values for 99% vs. 98%
is always more than 10%, regardless of the df.)
Since m.o.e. is the product of t* and s.e., and since the confidence
level (percentage) does not affect s.e., we can
conclude that m.o.e. is directly proportional to t* when the only thing changing is the
confidence level. But how can this be? How
can such a small change in confidence level (namely, a change from 98% to
99%) make such a large change in the width of the confidence interval?
Your answer to #3 will not be collected, but you may be randomly called upon.
Block 4: No class.
|
|
|
F 3/13/15
C
|
Last day of Q3.
Block 3: No class.
Block 4 HW due: See yesterday’s calendar entry for Block 3.
|
|
|
|
Spring break.
|
|
|
M 3/30/15
D
|
Classes resume.
Quiz or Graded Discussion on your
spring-break reading book is possible today or later in the week. Most of you
read How to Lie with Statistics,
which is a quick read (and very timely, despite its seemingly dated
illustrations and dollar values). Some of you read other books, and those
will require an alternative form of assessment.
|
|
|
T 3/31/15
E
|
HW due (both
classes): Pretend that you were given 11 SRS’s of M&M’s from different
parts of the country and that you were asked to see if there was enough
evidence to reject this null hypothesis:
H0: The true (unknown)
proportions of colors for the 11 populations from which these samples were
drawn follow the same pattern. [In other words, the true color proportions
are homogeneous across the 11
populations.]
Ha: The true proportions
of colors are not homogeneous across the 11 populations.
Here are the data you are given to work with:
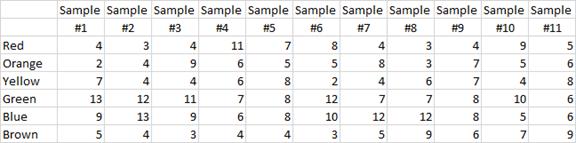
Perform the test, showing at least part of the computation of the 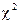 test statistic.
(Don’t show all the work; that would be cruel! Let your calculator’s 2-way test statistic.
(Don’t show all the work; that would be cruel! Let your calculator’s 2-way  procedure do most of
the work. Remember that the expected count for each cell is given by the
formula rowtot · coltot/grandtot.) procedure do most of
the work. Remember that the expected count for each cell is given by the
formula rowtot · coltot/grandtot.)
Execute all the PHA(S)TPC steps, and explain why df
= 50 in this problem. Be sure to check assumptions; you need 11 independent
SRS’s and all expected counts equal to 5 or more.
|
|

