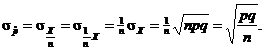|
M 12/2/13
|
Classes resume. No
additional HW due.
|
|
|
T 12/3/13
|
No additional HW due. Get plenty
of sleep. The busiest 3 weeks of the school year are upon us, and we need as
much energy as possible.
If you wish to study the probabilities of the hands of 5-card draw poker
(widely available via Google searching), you will have a leg up on everyone
else. However, that is optional.
|
|
|
W 12/4/13
|
HW due: Read pp. 414-421;
write p. 423 #7.88abc.
|
|
|
Th
12/5/13
|
HW due: Read pp. 445-449
twice; write pp. 449-450 #8.3, 8.4.
|
|
|
F 12/6/13
|
HW due: Read pp. 450-459;
write pp. 460-461 #8.11, 8.12, 8.14, 8.18, 8.20. Important: Insert the word “infinite” before the word
“population” in #8.18.
|
|
|
M 12/9/13
|
HW due:
1. Read pp. 461-466.
2. Rewrite the tan and green boxes on p. 465 in “AP style” as described in
the handy translation guide below. (You can make the edits directly in your
textbook if you prefer.)
3. Write pp. 466-467 #8.23, 8.24.
4. Use additional time (and you should have some) to finish up any missing
problems from Friday’s assignment.
HANDY TRANSLATION GUIDE (previously
presented in class)
When your book says . . . 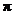
. . . AP students need to write p
instead. In other words, the population parameter (true probability) equals p.
When your book says . . . p
. . . AP students need to write 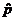 instead. In other
words, the statistic (sample proportion) equals instead. In other
words, the statistic (sample proportion) equals 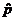 . .
Note: When answering question
#8.24, use the rule of thumb that np and nq must both be at least 10. Our standard notation for
population size is N, and our standard
notation for sample size is n. Also
note that the book has implicitly assumed that all of the populations are at
least 10n. Why? Answer: We learned
earlier that sampling with replacement (i.e., independent trials) is closely
approximated by sampling without replacement when 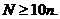 That should already
be in your class notes. That should already
be in your class notes.
|
|
|
T 12/10/13
|
No school (snow day).
Note: Wednesday’s assignment is still
due on Wednesday.
|
|
|
W 12/11/13
|
HW due: Read chapter
summary (pp. 469-470); write p. 470 #8.32-8.37 all.
|
|
|
Th
12/12/13
|
HW due: Read pp. 475-480;
write pp. 481-482 #9.1-9.4 all, 9.7abc.
|
|
|
F 12/13/13
|
HW due: Read pp. 482-492. Do
the reading twice if possible, and read the paragraphs below. Figure 9.4 on
p. 487 is of key importance.
Paragraph of High Importance:
When we compute a confidence interval for a parameter, we do not say that the
probability is 95% (or whatever the
confidence is) that the interval contains the true parameter, because probability is long-run relative
frequency, and if we are talking about a single confidence interval, there is
no “long run” involved. Instead, we say we are 95% (or whatever the
confidence level is) confident,
because we have used a method that gives correct results 95% of the time.
That’s what you need to remember. We reserve the word “probability” for
situations that involve a long-run relative frequency, and we use the less
precise words “chance” or “likelihood” or “confidence” when we do not have a
long run.
Tying Up Loose Ends from the End of
Class on 12/12:
For a normal data distribution, where the mean is 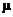 and the s.d. is and the s.d. is 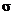 , the sampling distribution of , the sampling distribution of 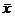 has mean has mean 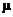 and s.d. and s.d. 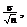 as we learned. (For
non-normal distributions, the sampling distribution of as we learned. (For
non-normal distributions, the sampling distribution of 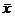 has mean has mean 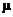 and s.d. of approximately and s.d. of approximately 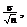 and by the CLT, that
approximation gets better and better as n
grows larger.) and by the CLT, that
approximation gets better and better as n
grows larger.)
But what about the sampling distribution of 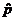 ? Does the same rule still hold? ? Does the same rule still hold?
Well, let’s think about this. The sample proportion, 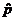 , is computed as , is computed as 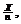 where X denotes a random variable that
counts the number of successes in n
independent trials. Since X is binomial,
and since the binomial approximation is approximately normal as long as np and nq are both at
least 10, we can say that the sampling distribution of where X denotes a random variable that
counts the number of successes in n
independent trials. Since X is binomial,
and since the binomial approximation is approximately normal as long as np and nq are both at
least 10, we can say that the sampling distribution of 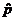 is approximately
normal with mean equal to the expected value of is approximately
normal with mean equal to the expected value of 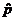 and s.d. equal to and s.d. equal to
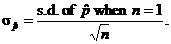
Using the formula we learned previously for the s.d.
of a binomial random variable, the numerator of that expression is 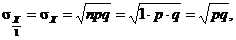 and when we divide by
the denominator as shown, we get and when we divide by
the denominator as shown, we get
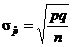 as claimed. (Q.E.D.) as claimed. (Q.E.D.)
This resolves the question that Nathan G. asked at the end of class
yesterday.
Not convinced yet? Here is a somewhat easier proof. Remember that 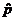 , the sample proportion, is defined to be the number of
successes (X) divided by the number
of trials (n). We learned in a
previous chapter that the standard deviation of a constant multiple of a
random variable is equal to the constant times the s.d.
of the random variable. (This is common sense: For example, the s.d. of a collection of heights measured in inches is 12
times the s.d. of the same data measured in feet.) , the sample proportion, is defined to be the number of
successes (X) divided by the number
of trials (n). We learned in a
previous chapter that the standard deviation of a constant multiple of a
random variable is equal to the constant times the s.d.
of the random variable. (This is common sense: For example, the s.d. of a collection of heights measured in inches is 12
times the s.d. of the same data measured in feet.)
Therefore, 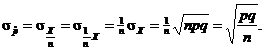 (Q.E.D.) (Q.E.D.)
|
|
|
M 12/16/13
|
HW due:
1. Write pp. 492-493 #9.11-9.15 all.
2. Start Tuesday’s assignment, since it will take you more than one evening.
|
|
|
T 12/17/13
|
HW due: Prepare a review
sheet for Wednesday’s test. If it is worthy, you will be allowed to use it as
a reference during the test. Limit yourself to one sheet, front and back. You
may write as large or as small as you wish.
In class: Inspection of study guides, followed by general review.
|
|
|
W 12/18/13
|
Test (100 pts.) through §9.2.
|
|
|
Th
12/19/13
|
No additional HW due.
In class: Guest speaker, Ms. Suzanne Schroer from the Nuclear Regulatory
Commission.
Tonight: Please attend Lessons & Carols.
|
|
|
F 12/20/13
|
Make-up test in MH-102 for Alex, Karan, and Marcelo,
7:00 a.m. sharp.
Anyone else who was grossly dissatisfied with how he did on Wednesday is
welcome to take a short “booster problem” at 7:30 a.m. to demonstrate
knowledge and ameliorate the grade. This is not for people who got a B but
wish they had received an A; this is for people who got a D or an F but wish that
they had passed. If you show up at 7:30 and are not in the “desperately
needing grade help” category, there is no penalty, but you will probably be
politely sent off to your A period class. If you fail to appear but are in the “desperately needing grade
help” category, your semester comment will convey that your metaknowledge is also poor.
In class: Moderately Fun
Friday! (No additional HW due.)
|
|