1. 0x1A0721237972616E6942

2. 2⁴⁰ or approximately 10¹² (about a trillion)

3. Throughput is about 50 MB/sec after deducting for error-correcting overhead. Divide 45 MB by (50 MB/sec) to get 0.9 seconds.

4. or almost 600,000 times larger


5. 2400 THz = 2.4 PHz = 2,400,000,000,000,000 cycles per second [deduct 1 point if commas are missing], or you could say 2.4 quadrillion cps

6.(a) Lead digit is 8 or greater.
   (b) Twos complement is 0x7000000000000557 = 7(16¹⁵) + 5(16²) + 5(16) + 7 = 8,070,450,532,247,930,199, but we must use a negative sign.
       Final answer: –8,070,450,532,247,930,199.
       [Note: There will be no qword conversions on the real test, since most calculators can’t handle
       that many significant digits.]

7. –8,070,450,532,247,930,198 = 0x8FFFFFFFFFFFFAAA

8. adding the twos complement of Y to X [deduct 1 point if “complement” is misspelled with an “i”]

9.(a) dword
   (b) 0000 0000 0000 0001 1100 0101 1000 1101
   (c) 1(16⁴) + 12(16³) + 5(16²) + 8(16) + 13 = 116,109

10.(a) –229
   (b) –174 = 0xFF52
   (c) See work below. Answer is 0xFF1B since we discard the leftmost carry, the one that exceeds
       the capacity of the “word” format that we are using. That’s the rule for twos complement.

  111
 0xFFC9
+0xFF52
0x1FF1B

   (d) How do we decode 0xFF1B? First, note that the lead digit is 8 or greater.
       Take the twos complement to get 0x00E5 = 14(16) + 5 = 229.
       Since the answer must be negative, we have –229 as required. Hooray!

11. Unicode, 16, double
     8, 2
     2¹⁰²⁴ = 2^{10 · 102.4} = (2¹⁰)^102.4 (10³)^102.4 = 10^{3 · 102.4} = 10^307.2 10³⁰⁷
MoDd

12. faster, parts, crash
     0110 0011 0110 0001 0111 0010 = 0x636172
     car
steganography

13.(a) 0 revolutions per second, since each new frame will “see” an identical-looking wheel after
       exactly 2 spokes have passed
   (b) 60/24 = 5/2 = 2.5 spokes per frame, which looks like 0.5 spokes per frame since the eye can’t
       see anything between frames
       Answer: 0.5 spokes per frame = 12 spokes/sec = 2 revolutions per second
   (c) If the wheel seemed to advance less than half a spoke per frame, the eye would interpret the
       closer of the two nearest spokes in the next frame as being the indicator of the direction of
       motion. However, with each frame advancing exactly half a spoke, the eye cannot decide
       which direction the wheel is moving without additional context clues. [The general term
       for a situation in which undersampling leads to misinterpretation of frequency is called
aliasing. A synonym that one occasionally encounters for aliasing is foldover (especially,
       as we saw in class, in the case of audio aliasing, where musical notes are rendered at the
       wrong pitch because of undersampling).]

14.(a) 0x464C414E
   (b) 0x53544131
   (c) Bitwise XOR produces 0x1518007F
       [It is not necessary to show all the work, but we’ll show a few of them. Remember that the
       symbol means the same as XOR. The first pair of hex digits, 4 XOR 5, would give us
       4 5 = 0100 0101 = 0001 = 0x1.
       The second pair, 6 3, gives us 0110 0011 = 0101 = 0x5.
       The final pair, E 1, gives us 1110 0001 = 1111 = 0xF.
       As for the rest, you can do them on your fingers.]
   (d) Suppose that the hacker knows both the key (K = 0x53544131) and the encrypted message
       (E = 0x1518007F). Since the plaintext message P satisfies the equation P K = E, and since
       the operation is both associative and commutative, we can easily solve this equation with
       algebra (believe it or not!):
P K = E
          (P K) K = E K      [XORing each side of the equation with K]
P (K K) = E K      [since XOR is associative]
P 0 = E K              [since anything XORed with itself is 0]
P = E K                    [since 0 XORed with anything does not change the original message]
P = 0x1518007F 0x53544131 [by substitution]
P = 0x464C414E              [by performing the bitwise XOR]
P = “FLAN”                   [by ASCII table]
       [Or, since we learned in class that the operation is its own inverse, you could simply XOR
       the encrypted text with the key, and your work would consist of showing some of the bitwise
XORing and explaining why you were doing that. Most of the work of XORing can be done
       on your fingers; there is no need to show all of it on your test paper.]

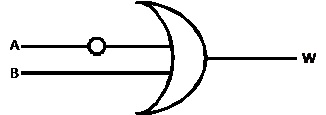
15.(a)


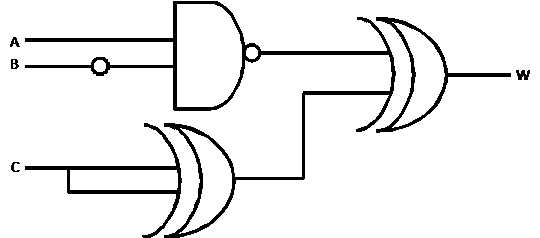
   (b) Since anything XORed with itself is 0, we have this:






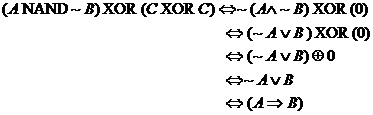
       (Q.E.D.)
       That’s the end of the proof if you recall the IMP gate’s definition: “A IMP B” is equivalent to
       saying that A is false or B is true.

       Or, if you prefer a truth table proof, you can certainly do it this way:

A	B	C	C	~B	A ~B	A NAND ~B	C XOR C	(A NAND ~B) XOR (C XOR C)	A B
1	1	1	1	0	0	1	0	1	1
1	1	0	0	0	0	1	0	1	1
1	0	1	1	1	1	0	0	0	0
1	0	0	0	1	1	0	0	0	0
0	1	1	1	0	0	1	0	1	1
0	1	0	0	0	0	1	0	1	1
0	0	1	1	1	0	1	0	1	1
0	0	0	0	1	0	1	0	1	1

       Since the last two columns are the same in all cases, the expressions are equivalent. (Q.E.D.)

   (c)

Scoring Guidelines

Note: The “points possible” add up to 102. That means that you can miss one of the smaller questions without penalty. Also note that minor errors are excused without penalty in some of the questions, especially if work is shown clearly.

Question #	Points Possible	Partial Credit Scoring Rubric
1	3	Deduct 1 point if byte order is wrong. Deduct 1 point for each additional significant error. Omitting the bell (0x07) is a point; omitting the Ctrl+Z (0x1A) is a point. Minor errors (e.g., looking up one or two of the codes incorrectly) are no penalty.
2	4	Half credit (2 points) if one answer is missing. Both 2^40 and 10^12 are required. It is acceptable to say “1.0995 trillion” or “1.1 trillion” instead of 2^40, and it is acceptable to say “1 trillion” instead of 10^12. There is no partial credit for mistakes here.
3	3	Deduct 1 point for using 8 bits = 1 byte. That is true in RAM and permanent storage, but not in telecommunications, where there is always some overhead for error correction. We use the rule of thumb of dividing bps by 10 to get bytes per second. Thus the throughput is only about 50 MB/sec, not 62.5 MB/sec. The answer for students who incorrectly divided bps by 8 would be about 0.72 seconds for the transfer time.
4	3	Deduct 2 points for missing or confusing work, even if the answer is correct. Deduct an additional 1 point if answer is wrong. Any answer between 500,000 and 600,000 is acceptable, as long as the work is understandable.
5	3	It is acceptable to write “2.4 quadrillion cps” or “2400 trillion cps.” Deduct 2 points if answer is around 2.7 quadrillion or 2,700,000,000,000,000 cps. Deduct 3 points for any other answer. Also, deduct 1 point if answer has more than 4 digits and is missing commas.
6(a)	2	Deduct 1 point for saying that the criterion is that the lead digit should be greater than 8. That is wrong. We check to see if the lead digit is 8 or more.
6(b)	6	Score 5 points for work, 1 point for answer. Forgetting to take the twos complement (and thus obtaining a positive number for an answer) is a major error—6 points off. Taking the twos complement but forgetting to put a minus sign in the final answer is a 2-point penalty. Forgetting to add 1 when computing the twos complement is another 2-point penalty. Skipping the lead digit (7) when computing the value is a 1-point penalty. There is no penalty for other minor arithmetic errors if the work is shown clearly.
7	4	Score 2 points for each. ECF credit (no point penalty) if decimal answer is wrong but matches a wrong answer obtained in #6(b). No credit for decimal answer if no answer was obtained in #6(b). Note that the hex value can be produced even if #6(b) was omitted.
8	3	Wording should be almost exactly as shown in answer key above. Deduct 1 point if “complement” is misspelled with an “i.”
9(a)	2	No partial credit. The only acceptable answer is dword.
9(b)	2	Deduct half a point for each error. The leading zeros are required.
9(c)	4	Score 2 points for work, 2 points for answer. No credit for answer, even if correct, if work is confusing or missing. If work is clear, minor errors are excusable with no point penalty.
10(a)	2	No partial credit.
10(b)	3	Score 3 points for correct answer (0xFF52). Work is not required. However, if answer is not 0xFF52, deduct 1 point for each error, but only if work is shown. If answer is not 0xFF52 and work is illegible, confusing, or missing, there is no credit.
10(c)	3	Score 3 points for correct answer (0xFF1B). Work is not required. However, if answer is not 0xFF1B, deduct 1 point for each error, but only if work is shown. If answer is not 0xFF1B and work is illegible, confusing, or missing, there is no credit. ECF credit (no penalty) if answer is wrong but is consistent with a wrong answer to #10(b).
10(d)	3	Any clear, correct work leading to –229 is acceptable. Deduct 2 points if work is unclear, incorrect, or does not lead to –229.
11	16	Score 2 points per blank. No partial credit, except for the last one (“MoDd”), where half credit is possible if there is only one error. Writing “MOdd” or something similar (with upper and lower case incorrect or not clearly shown) counts as a single error.
12	10	Score 2 points per blank. No partial credit, except for the word “parts,” which can be replaced with an equivalent concept (“disks,” “platters,” or “whirring chunks of metal”) without penalty, and for the word “car,” which can receive half credit if there is only one error.
13(a)	2	OK to say “motionless” or something similar to that. Work is not required.
13(b)	2	Half credit if correct answer is given in spokes per frame or some other units that were not requested. No credit for saying 2.5 spokes per frame, since that shows a lack of awareness of how aliasing works.
13(c)	2	Half credit for a general awareness of aliasing. Full credit requires knowing that the eye can’t judge which spoke is closer if there is a half-spoke change with each frame. Note that full credit is possible here even if the answer to #13(b) was wrong.
14(a)	2	Deduct 1 point for each error.
14(b)	2	Deduct 1 point for each error.
14(c)	3	Deduct 1 point for each error, except that if some scratch work is shown, the first 2 errors are excused without penalty.
14(d)	3	Any believable explanation (as long as it includes at least one complete sentence) that includes an awareness of the need to XOR the encrypted message with the stolen key is acceptable. Add a bonus point if explanation actually leads all the way back to the starting point (FLAN). Deduct 1 point if explanation does not include a complete sentence, another 2 points if explanation is spotty.
15(a)	3	Deduct 1 point for each error.
15(b)	3	Deduct 1 point for each major error. Minor errors in the proof (either algebraic or truth table proof) are excusable.
15(c)	4	Deduct 2 points if OR gate is missing or shown as some other type of gate. Deduct 2 points if inverter is missing or is on the wrong input.