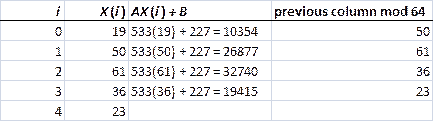|
F 11/1/13
|
Last day of Q1.
HW due:
1. Read §6.1 (pp. 299-303) and §6.2 (pp. 305-311).
2. Write up a protocol for storing
the state of a Monopoly game using some combination of integers and ASCII text.
See the example below for one possible protocol for storing the state of a
tic-tac-toe game of any size. Note:
Try to exhibit some encryption, some data compression, and some possibility
for error detection in your protocol. Encryption
means that the format should look like gobbledygook to a person who does not
own your game software. (Weak encryption is acceptable.) Data compression means that the game state storage file should,
at a minimum, take fewer bytes than would be needed to describe every aspect
of the game in plain English. (We will see better compression techniques
later in the course.) Finally, error
detection means that your protocol should contain a least a little redundancy so that some errors can be
caught by cross-checking. The example below illustrates encryption, data
compression, and error detection. You
do not have to be as detailed as this example. However, you need to specify
what you are storing, how many bytes you need for each object, and what
format you intend to use (integer, ASCII text, or other) for each object.
Example Protocol for Storing a (2D)
Tic-Tac-Toe Game of Arbitrary Size:
Header field (word, byte, word)
The first 5 bytes will
contain the dimensions of the board, as follows: Bytes 1 and 2 will be the
horizontal size (word format, integer, little-endian), byte 3 will be the
value 0x4D, and bytes 4 and 5 will be the vertical size (word format,
integer, little-endian). The value in bytes 1 and 2 can be cross-checked
against the value in bytes 4 and 5, since in any valid tic-tac-toe game, the
horizontal and vertical dimensions should be equal.
Player names (20 bytes)
The next 20 bytes contain
the players’ names, interleaved. The name of player 1 shall be stored in
bytes 6, 8, 10, 12, 14, 16, 18, 20, 22, and 24, and the name of player 2
shall be stored in bytes 7, 9, 11, 13, 15, 17, 19, 21, 23, and 25. Names are
stored in ASCII, but the interleaving makes the file slightly harder to hack.
Names longer than 10 characters are not allowed. It is assumed that player 1
is “X” and player 2 is “O”—however, “X” and “O” are not stored anywhere in
the file, since players can be reassigned between “X” and “O” simply by
changing whose name begins in byte 6. If a name is shorter than 10
characters, any character that is not needed shall be stored as 0x20 (ASCII
code for a space).
Grid contents (variable number of
bytes, determined by values already read)
Let m denote the integer value in bytes 1 and 2, i.e., the horizontal
dimension. The next m bytes of the
file, beginning with byte 26, contain the contents of the cells in the first
row of the tic-tac-toe board, stored in ASCII. For example, if m = 3 and the top row is XOX, than
byte 26 would be 0x58, which is the ASCII code for X, byte 27 would be 0x4F,
which is the ASCII code for O, and byte 28 would be 0x58 again. A cell that
is not occupied yet shall be represented by the ASCII code 0x20 (space).
Let n denote the integer value in
bytes 4 and 5, i.e., the vertical dimension. Repeat the process described in
the previous paragraph for a total of n
rows.
Player indicator (1 byte)
Whose turn was it at the point where the game was suspended? We have to
record this somewhere. The next byte will contain either “X” or “O” to
indicate which player will be the next to play. If the game is a “scratch
game” or has already been won by one of the players, then this byte will
contain the hex value 0x5A (ASCII code for Z) to indicate that nobody can go
next.
End of file (5 bytes)
At this point, the file contains 5 + 20 + mn + 1 = 26 + mn bytes of
data. We will add 5 more bytes at the end, bringing the total to 31 + mn bytes. The
final 5 bytes in the file shall consist of the file size (31 + mn) expressed
as a dword hex integer, little-endian format,
followed by the end-of-file character, 0x1A. Storing the file size within the
file is redundant, since the operating system (Windows, OS X, etc.) already
keeps track of the file size. However, doing this provides a way of catching
some software glitches, since whenever the stored file size does not match
what the operating system thinks it should be, we know there is a problem.
|
|
|
M 11/4/13
|
HW due: Finish the
assignment that was due Friday. Because of Homecoming weekend, there is no
additional assignment, but you are expected to complete the Monopoly assignment
by today. We will discuss some of the better ideas in class.
|
|
|
T 11/5/13
|
No class.
|
|
|
W 11/6/13
|
HW due:
1. Read §6.7 (pp. 337-344). Reading notes are required, as always.
2. Write a paragraph of English text (minimum of 80 characters) in all upper
case, with no punctuation. If you are not feeling particularly creative, you
can take any block of text you find anywhere, and if you prefer not to write
it down on paper, feel free to type it. If you are a poor typist, you may
copy and paste it.
3. Use an imaginary coding wheel similar to the ones on pp. 338-339 to encode
your paragraph using a rotational cipher. You can use the wheels found there,
or if you want to be a little bit sneakier, you can imagine shifting the
inner ring to the left or the right. You can also write 2 alphabets above and
one below, like this:
ABCDEFGHIJKLMNOPQRSTUVWXYZABCDEFGHIJKLMNOPQRSTUVWXYZ
ABCDEFGHIJKLMNOPQRSTUVWXYZ
The key is “W” or –4 in this example, since the lower alphabet has been
shifted 4 positions to the left so that A matches “upward” to W. The way you
would use this is to read from the bottom to the top. For example, the word
FOOTBALL would be encoded as BKKPXWHH since F matches “upward” to B, O
matches “upward” to K, and so on.
To make your encrypted text more sneaky, please don’t use W as your key. Use
something else!
4. Send your encrypted text to Mr. Hansen by e-mail. Be sure to begin your
subject line with __ (double underscore), and include your name in your
subject line, like this:
__MODD HW from Jones, Billy
|
|
|
Th
11/7/13
|
HW due:
1. Read §6.5 (pp. 331-334) and §6.6 (pp. 335-337).
2. Read this link
about check digits in Vehicle Identification Numbers (VINs).
3.
(a) Write down the VIN of a car that is either owned by you or is a car that
you can find readily on the street. The VIN is located on a plate on the
driver’s side of the dashboard and can be viewed by standing at the front
left of the car and looking down toward the point where the windshield meets
the hood of the car. If you can’t find the VIN, try a different car. All cars
manufactured within the past 40 years have a VIN.
(b) Verify that the check digit (digit 10) of the VIN you wrote down is
correct. Show your work!
5. On the same homework sheet, write answers to #7 and #8 from p. 335 of your
textbook.
|
|
|
F 11/8/13
|
No school (faculty work
day).
|
|
|
M 11/11/13
|
HW due:
Read this
article several times, with a pencil and a calculator by your side. The
article is difficult, but if you work it out, carefully and systematically,
you can understand most of it. This will take you more than an hour. Be sure
to budget your time appropriately. If you encounter an abbreviation with
which you are unfamiliar, visit Wikipedia or follow the links within the
article.
Important: Be sure to read all 3
pages of the article.
In class: An Open-Notes Quiz on
the reading is likely. Handwritten reading notes are permitted, but a
printout of the article is not. The quiz will not cover the most difficult portions of the article, since we
will need to cover those topics in class. Instead, the quiz will cover the
basic terminology and the overview of the concepts.
|
|
|
T 11/12/13
|
No class.
|
|
|
W 11/13/13
|
HW due:
1. Read §6.3 (pp. 313-323), taking care to ignore the formula at the bottom
of p. 321. We will discuss the formula in class, but for now, don’t get
bogged with trying to understand it. Read all the rest of the section,
however. You do need to know the term entropy.
Note that information-theoretic entropy, which is what we are learning about,
is different from thermodynamic entropy, which is a concept from physics.
2. Write #3, 4, 8, and 14 on pp. 324-325. For full credit, your HW must be
written on 3-hole punched paper (not spiral-bound paper) and must conform to
the format requirements. There is a small point
penalty for assignments that do not meet the requirements. It is acceptable
to use micro-perforated spiral-bound paper, provided you remove the paper
before class and place it in your 3-ring binder.
|
|
|
Th
11/14/13
|
HW due:
1. Read §6.4 thoroughly. An open-notes quiz on this material is likely.
2. Skim §6.8. (In other words, read it only for a general overview, not in
detail.) We will need to read this section several more times over the next
few days, because it is difficult.
3. Write #1-5 on p. 331. Note: For
#3 and #4, use the fact that each extra bit of storage (per sample) accounts
for 6 dB of dynamic range. For #5, do not compute an exact answer; a
“ballpark” estimate is preferred for #5, but show your work.
|
|
|
F 11/15/13
|
IMPORTANT: Do not enter MH-102 during the
CyberPatriot competition. Today’s class will be held in room MH-103 instead.
HW due:
1. Reread §6.8. This is difficult material that will need to be read several
times. Note: As part of your HW
assignment, correct the typo in the 5th line of p. 353: the phrase “powers of
1” should be “powers of 17” instead. You can make the change in ink if you
wish.
2. Finish the chart in the lower right corner of p. 352. In this chart, C = 5, N = 17, and the values of J
should go from 0 all the way to 17, instead of only to 6.
3. Compute 507735 mod 23. (In other words, find the remainder when
507735 is divided by 23.) Show your work.
Hint: This will cause overflow on
any standard calculator. The only reasonable way to work around that problem
is to find the intermediate results mod 23, mimicking the technique you used
in #2. The first few steps are shown below to get you started. When you do
your writeup, use a table to save writing, but show
each step. (The full-sentence explanations are not needed as part of your HW,
but please read them!)
Let C = 5077, J = 0 to 35, N = 23.
Step 0: C0 mod N means to take the remainder when 1
is divided by 23. The answer is 1.
Step 1: C1 mod N
means to take the remainder when 5077 is divided by 23. The answer is 17.
[Warning: Make sure you understand
how to get 17 before proceeding. If you can’t get 17 as the remainder when
dividing 5077 by 23, phone a classmate or contact Mr. Hansen immediately!]
Step 2: C2 mod N
could be computed as 50772 mod 23, but that involves huge numbers.
Instead of multiplying 5077 by 5077, we take the previous result, 17, and
multiply that by 5077. The answer
is 86,309, and 86,309 mod 23 = 13.
Step 3: C3 mod N
could be computed as 50773 mod 23, but that involves really huge numbers. Instead of
multiplying 5077 by 5077 by 5077, we take the previous result, 13, and
multiply that by 5077. The answer
is 66,001, and 66,001 mod 23 = 14.
Step 4: C4 mod N
could be computed as 50774 mod 32, but that involves incredibly huge numbers. Instead of
multiplying 5077 by 5077 by 5077 by 5077, we take the previous result, 14,
and multiply that by 5077. The
answer is 71,078, and 71,078 mod 23 = 8.
Step 5: C5 mod N
could be computed as 50775 mod 32, but that involves super-incredibly huge numbers. Instead
of multiplying 5077 by 5077 by 5077 by 5077 by 5077, we take the previous
result, 8, and multiply that by
5077. The answer is 40,616, and 40,616 mod 23 = 21.
|
|
|
M 11/18/13
|
HW due:
1. Read §6.8 a third time. This is difficult material, but hopefully some of
it is starting to make sense, now that we have done some of the exercises in
detail.
2. If you haven’t already completed last Friday’s assignment, then please do
so! Not only will it be graded a second time, but you need to know the
techniques in order to do the assignment that we will do in class on Monday.
3. Work through Example 6.17 on p. 353 with pencil and paper and a calculator
by your side. Then answer the following questions:
(a) If P denotes your public key,
what does Q denote in this example?
(b) If I denotes your private key,
what does J denote in this example?
(c) What is so remarkable (useful) about the fact that QI and PJ,
when considered mod N, are equal?
4. Use X(0) = 19, not 125, to
repeat Example 6.15 for the first 4 numbers from the PRNG. Let A = 533, B = 227, and N = 64 as
in that example. The only change is that you will use the “shared secret”
from #3, namely 19, as the seed.
|
|
|
T 11/19/13
|
No class.
|
|
|
W 11/20/13
|
HW due:
1. Correct your answers from Monday’s assignment. The answer key is posted
below.
2. A spare copy of your private key has been e-mailed to you. Do not share
your private key with anyone. Here is the table of public keys:
Andrew: 11
Beau: 2
Coby: 16
Gabe: 19
James: 5
Justin: 6
Matthew: 21
Max: 3
Michael: 14
Nate: 13
Ryan: 12
Shane: 8
Thomas: 4
(a) Let P denote your own public
key. Compute P22 mod 23,
showing each step. Use a table exactly like the one below. (In this example,
the value of P is 15, which is not
giving anything away, since nobody’s public key value is 15.) Can you learn
from an example? Hopefully, you can. Simply look at what is being done at
each step in this example. Of course, your P value is not 15, so you will have to make the appropriate
adjustments when producing your table.
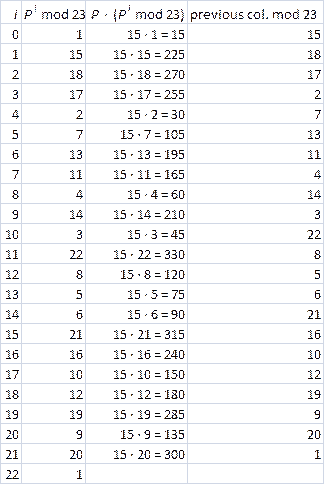
In the example table above, the answer (i.e., 1) is shown at the beginning of
the final row. The last column of each row becomes the Pi mod 23 entry in the next row.
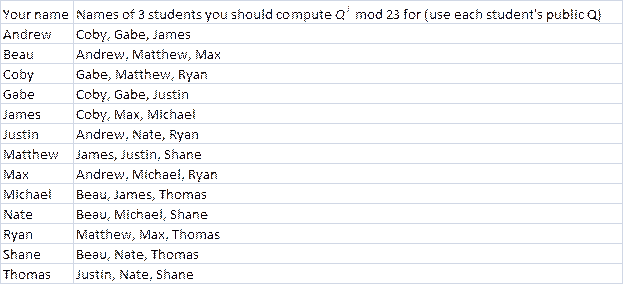
(b) Let Q denote another student’s
public key, and let I denote your
own private key. Compute QI
mod 23 for 3 different students, as shown by the table below. You do not need
to show your work. You can perform the work on a calculator or on a
spreadsheet if you wish. You are encouraged to contact some or all of your 3
other students in order to check that they obtained the same results that you
did. In most cases, you will obtain 3 different answers, although it is
possible that 2 of your answers may be the same since we are using such a
small keyspace.
Answer Key to HW Assignment due
Monday, 11/18/2013
Correct your answers, using a different color. For example, if your original
was in pencil (as it should be), you could use a pen with blue ink to make
your corrections.
3. First, you should copy the information from Example 6.17 on p. 353. Most
people forgot to do this!
You need to show the work that leads to obtaining the seed
value of 19 in both cases.
(a) Q = the other
person’s public key
(b) J = the other
person’s private key
(c) QI
mod 23 = a secret seed using person 2’s public key and person 1’s private key
PJ mod 23 = a secret seed using person 1’s public key
and person 2’s private key
It is magical and useful that
QI mod 23 = PJ mod 23, because now
person 1 and person 2 are sharing a
secret seed that they can use
for long, long XOR encryption (gigabytes worth, if necessary), even though
no secret key was ever passed
between them. If the keyspace is sufficiently
large, and if the private keys
are kept secret, no hacker
will be able to read the XOR-encrypted data! [Note: Our little example in class
has a keyspace
of only about 20 usable keys, so it would be no good for “real world” use. We
would need
a keyspace
of hundreds of trillions of trillions of trillions of possibilities before we
could ever dream of
claiming that we had any sort
of serious security. A truly hacker-proof encryption scheme would require
a much larger keyspace than that, and an “NSA-proof” scheme would
require  .] .]
4. Let A = 533, B = 227, N = 64, X(0) = 19.
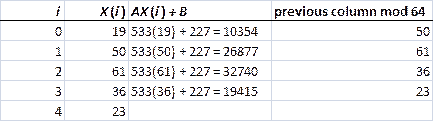
The answer for X(4) (i.e., 23) is
shown at the beginning of the final row. The last column of each row becomes
the X(I) entry in the next row.
[The pattern could be continued to generate as many random X(i) values as necessary. This
particular scheme is not very good, since it will repeat after a maximum of
64 entries in the table and will hence become predictable. However, we could
use a larger modulus, and there are also more sophisticated methods that use
“feedback” from the data so that repetition is squeezed out. For example, you
can see here that every time the number 50 appears, 61 will be the next
number in the list. However, there are ways—not covered in MODD—for feeding
data back into the loop so that the next time 50 appears, something other
than 61 would probably be the next number. If you want to know more, see the
Wikipedia articles on stream
ciphers and block
ciphers. Both articles go far beyond the scope of our course.]
|
|
|
Th
11/21/13
|
Quiz (70 pts.) on all recent material.
Skills that will be tested:
1. SNR and dynamic range calculations:
6 dB per bit.
Sample problem: Compute dynamic range for 16-bit
audio samples. Answer: 16 · 6 dB = 96 dB.
The other dB calculations (converting ratio to dB,
converting dB to ratio, or using dB or ratio to convert power level from
input to output or vice versa) will be covered on a quiz next week.
2. modulo arithmetic: Given any
integers M and N, compute M mod N quickly and efficiently—no muss, no
fuss.
3. PRNG implementation:
You will be given parameters A, B, N, and a seed value X(0).
Your task is to find X(i)
for any i,
where X(i) = [AX(i)
+ B] mod N. Note: By X(i) we mean the ith output of
the PRNG.
4. exponentiation: Given any
integers L, M, and N, be able to
compute LM mod N, showing your work.
5. public key encryption:
Given any core value C, modulus N, and
private keys I and J, compute public keys P = CI mod N, Q = CJ mod N.
Given someone else’s public key, use your own private
key to compute the “shared secret” QI
mod N = PJ mod N.
Optional: Given someone else’s public key and
knowledge of a too-small keyspace, recover his
private key.
6. data compression:
Given a protocol for run-length encoding, be able to
convert from compressed to uncompressed or vice versa.
Compute input and output sizes (in bits) for
run-length encoding.
Compute compression ratio or compression percentage.
Compression ratio = input size : output size.
Compression percentage = 100 · (output size – input
size) / output size.
Note: You are not required to
verify the check digit of a VIN. However, if a simpler error-detection
protocol is given to you, you should be able to implement it. For example,
you should be able to identify which of the following 9-bit blocks contains a
parity error when using even parity:
010010011
101010100
111111110
010110110
Terminology that will be tested:
coding, data compression, error-correcting codes, encryption, cryptanalysis,
VIN, ISBN
error detection, error correction, check digit, parity, even parity
data compression, run-length encoding, lossless compression, lossy compression, masking, ZIP, compression ratio
dynamic range, signal-to-noise ratio
key, keyspace, PKI, public key, private key,
plaintext, ciphertext, ECC (elliptic curve
cryptography)
XOR encryption, PRNG (pseudorandom number generator), seed
|
|
|
F 11/22/13
|
HW due:
Compute the “shared secret” that you have with everyone else in the class.
Recall their public keys from above:
Andrew: 11
Beau: 2
Coby: 16
Gabe: 19
James: 5
Justin: 6
Matthew: 21
Max: 3
Michael: 14
Nate: 13
Ryan: 12
Shane: 8
Thomas: 4
Note: If you have shown your work
previously, you are permitted to do this assignment by an automated process
(spreadsheet, calculator, or computer program), and all you need to write
down on your HW paper is your answers. For example, here is a calculator
process that works well for the TI-83 or TI-84:
1. Store your private key into variable I. For example, if your private key
is 7, you would key in 7 ALPHA I ENTER. You need to do this only once. ALPHA I ENTER. You need to do this only once.
2. Store the other person’s public key into variable Q. For example, the
keystrokes for communicating with Andrew would be 11 ALPHA Q ENTER. ALPHA Q ENTER.
3. Store 1 into the answer variable, A. Use the same general idea as in steps
1 and 2.
4. Key in AQ–int(AQ/23)*23 A ENTER to compute Q1 mod 23. Remember that “int” is found under 2nd CATALOG. A ENTER to compute Q1 mod 23. Remember that “int” is found under 2nd CATALOG.
5. Press ENTER a second time to find Q2 mod 23.
6. Keep pressing ENTER, as needed, until you have pressed ENTER the
appropriate number of times for your private key, I. For example, if your
private key is 7, you would press ENTER a total of 7 times.
7. At this point, the display should be showing the answer, namely QI
mod 23, which is the shared secret that you have with the student whose
public key you entered in step 2.
8. Repeat steps 2-7 for each classmate. You will probably want to
double-check the 3 classmates you already did in the earlier assignment. Helpful hints: Don’t forget step 3.
You have to reset the answer variable each time. Also, since step 4 is
tedious to key in, you can save a lot of time by using 2nd ENTRY 2nd ENTRY as
needed to recall the line where you entered step 4; then press ENTER to
execute it.
|
|
|
M 11/25/13
|
HW due: Prepare a short
project proposal, approximately half a page, in which you state a topic of
interest that you would like to research. Describe what your learning
objective is and the type of deliverable product (e.g., PowerPoint slide
show, written document, working model built out of Lego blocks) you intend to
produce. If there are additional resources or support that you anticipate
needing, be sure to list those as well. Important:
The topic must be of personal interest to you. Enthusiasm is preferred. Keep
the project small enough that you can realistically complete it by Wednesday,
January 8.
If Mr. Hansen were about 35 years younger, here are some topics he would be
personally interested in:
steganography
“man in the middle” hacking attacks
spoofing
digital signatures
cryptographic hash functions
PKI (a more “real-world” setup, much bigger than the keyspace
of size 20 we used in class)
statistical analysis of various types of PRNG
How much noise is too much? At what point do error-correcting protocols start
to break down?
dithering
audio aliasing
digital audio artifacts
QR codes
RFI tags
SMS (text) protocol
Below is an example of a project proposal. You may or may not be interested
in tokenization; that’s not the point. The purpose of this example is to show
the format and level of description that is expected in your proposal.
Learning objective: I would like
to learn how tokenization works. I propose to take the text of the New
Testament (available in digital form), separate it into individual words,
prepare a frequency chart, and develop tokens of suitable length for each
word. I will also prepare tokens for common pairs and triples of words (e.g.,
“from the,” “at that time,” “in the”) and experiment with various strategies
that produce varying compression ratios.
Deliverable product: A computer
file consisting of the repeat counts of all the tokenized expressions in the
New Testament, arranged in descending order by frequency, along with their
binary tokens under several different protocols and an Excel bar graph
showing the compression ratios achieved with each protocol. If I am unable to
get more than one protocol to work, then I will instead make my bar graph by
using a single protocol applied to several different translations.
Additional resources: I will need
to meet with Mr. Hansen in mid-December (Monday, Dec. 9 preferred) in order
to make sure that I am proceeding on the right path and to gain some
additional strategies for tokenization if the ones I have been using are not
giving compression ratios of at least 2.5:1.
|
|
|
T 11/26/13
|
Guest speaker, Mr. Joe Morris of MITRE Corporation.
Because this is not a regular class day, 8 bonus points will be awarded to
each student who attends.
|
|