|
T 10/1/13
|
No class.
|
|
|
W 10/2/13
|
HW due: Complete the previously assigned problems,
and do the somewhat simpler problems below. Collaborating with friends is OK,
provided you huddle with someone who has previously helped 0 or 1 students
with this assignment. If the person you are working with has already helped 2
or more other students, then you must find a “disciple” of his to help you.
Note: If you happen to come across
something that is always true, you can denote that with a “1” in your Boolean
algebra, and in your circuit diagram you can use a gate (e.g., 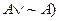 that is guaranteed
always to produce a true (1) output. On the other hand, if you happen to come
across something that is always false,
you can denote that with a “0” in your Boolean algebra, and in your circuit
diagram you can use a gate (e.g., that is guaranteed
always to produce a true (1) output. On the other hand, if you happen to come
across something that is always false,
you can denote that with a “0” in your Boolean algebra, and in your circuit
diagram you can use a gate (e.g., 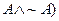 that is guaranteed
always to produce a false (0) output. that is guaranteed
always to produce a false (0) output.
4. Create a circuit diagram that implements the logic of an XOR gate. By way
of review, an XOR gate is the negation of the EQU gate, and an EQU gate is
true precisely when its inputs are the same—either both true or both false.
In other words, A EQU B returns 1 if 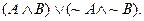 Translated into
plain English, we are saying “A is equivalent to B” if and only if (A and B
are both true) or (A and B are both false). Translated into
plain English, we are saying “A is equivalent to B” if and only if (A and B
are both true) or (A and B are both false).
For #4, your gate should have 2 inputs, labeled A and B, and an output,
W, that is the result of the XOR operation.
5. Make a table having 18 columns. (You may have to turn your paper sideways
to do this.) Label the first column as A, the second column as B, and the
remaining columns as the integers 0 through 15. Make a truth table that has
the following pairs for A and B, as we have always done: 1 1 for row 1, 1 0
for row 2, 0 1 for row 3, and 0 0 for row 4. Your table should now look like
this:

Next, start filling in the numbered columns with the binary values for 0
through 15. For example, the column labeled “0” would be
0
0
0
0
.
. . and the column labeled “1” would be
0
0
0
1
You can use “the chart” that you made earlier in the course to help you if
you wish. Be neat! This chart that you are making will become the basis of
our class notes today. Fill in all the columns.
|
|
|
Th
10/3/13
|
HW due:
1. Complete problems 1-3 that were assigned last week. Correct answers are
expected. Be sure you have copied #1 as given. For problems 2 and 3,
consulting other students for help is acceptable as long as you do not copy.
If the student you ask for help has already helped 2 other students, you need
to ask one of his “disciples” instead.
2. Write circuit diagrams for gates 11, 13, and 0 (IMP, RIMP, and FALSE) from
the chart you produced in class yesterday.
|
|
|
F 10/4/13
|
HW due: Read from the bottom of p. 43 to the
middle of p. 54. Reading notes are required, as always. (See the “HW
guidelines” link at top of schedule for the required format.)
IMPORTANT: Use
your remaining time to finish up the previously assigned problems. Anyone who
has not seen Mr. Hansen for help after school, or at least Gabe or one of his
“disciples,” will receive no partial credit in the event of errors.
|
|
|
M 10/7/13
|
HW due:
1. Read something interesting in your textbook (minimum of 5 pages), and be
prepared to report on it to the class. Hint:
It’s easy to tell if you have satisfied this assignment, since if it’s really
interesting (not merely “fake interesting”), you will have done some
additional research as well. Reading notes are required, and you can use them
when you give your short talk.
2. Prepare your previously assigned problems for submission and grading.
Neatness counts. If you received help from another student, you must describe
the specific help you received and
give the name of the student who helped you. Vague descriptions are not
acceptable.
|
|
|
T 10/8/13
|
No class.
|
|
|
W 10/9/13
|
|
|
|
Th
10/10/13
|
HW due:
1. The 4 students who are listed below need to work on both the original
message from yesterday and the new message that is given below. You must have
correct answers for both at the start of class. Use the same key as before.
BB: 0xF0C5852A37263912
SOET: 0x88BF33ACFBD8933E
MS: 0x140089CDE8988606
AT: 0xB60B89F02A2D91C9
2. One reason the simpleminded cryptographic system we have been using is no
good for “serious” use is that if a hacker intercepts the encrypted message
(which is easy to do) and happens to know some of the plaintext message, he
can recover part or all of the key. That, of course, is very bad, since if
the key is recovered, future messages sent using the same key will be
readable by the unauthorized hacker. A variation on this technique was
actually used during World War II, when the German U-boat crypto operators
got somewhat lazy and began many of their messages with predictable phrases
such as “Heil Hitler” or weather reports that had
many guessable words in them. Since the keys were occasionally being reused
(a real no-no!), American and British mathematicians who intercepted the
coded transmissions were then able to recover the keys in many cases, and
those key settings could be used to read other previously unknown messages.
Well, it’s a good thing for us! The American and British mathematicians were
able to shorten the war significantly. Estimates vary, but the war was
probably shortened by at least a year, and certainly hundreds of thousands of
lives were saved as a result.
Here’s your exercise: Write down your key (the one you received by e-mail)
and do not look at it. Now, prove that you can recover the key by using
only the original message you were sent and your knowledge of what the
plaintext message was. Check your answer only at the very end. To
help you, here are the plaintext messages from yesterday:
AbuDhAbi
amBusheD
genoTyPe
inUndAtE
YugOsLav
junCTioN
lonGwiSe
kipperED
koWtoWEd
kAtaKaNa
WAteRloO
cedilLaS
KAtmAnDu
3. (Optional, but fun!) See if you can recover another student’s secret key.
|
|
|
F 10/11/13
|
No school (faculty
professional day).
|
|
|
M 10/14/13
|
No school (Columbus Day).
|
|
|
T 10/15/13
|
HW due: Complete the practice test. An answer key is also available, but please
don’t peek until you have recorded timings for all the problems on the
practice test!
An ASCII table, similar to the one
you will be given during the test, is available.
If you have any trouble at all with the practice test, you need to see Mr.
Hansen before school, after school, or during C period. There is no regular
class today, but you need to show up if you have questions.
Hint: Don’t show up saying, “I
don’t understand how to do this problem.” Instead, bring a written record
showing a solid effort. Your written record must contain the following:
- All scratch work and partial attempts
- List of resources you have consulted (websites,
other classmates, textbook, etc.)
- Specific
questions you still have.
Note that all 3 components (scratch work, list of resources consulted, and
questions) must be in writing. If your written documentation is lacking, Mr.
Hansen won’t give you much help, and you’ll need to ask a classmate first
(someone who doesn’t demand written documentation, that is!).
Here are some examples of bad, mediocre, and good questions to ask:
Bad: Can you tell me how to do
this problem?
Mediocre: Do I need to take the
twos complement before starting this problem?
Good: I took the twos complement
and added, but the answer I got was off by 0x0001 compared to the answer I
received when checking against the Windows Calculator. Why is that?
|
|
|
W 10/16/13
|
HW due: Your practice test
will be collected, spot-checked, and graded.
In class: Review.
|
|
|
Th
10/17/13
|
Test (100 pts.) on all material for the entire
course so far. All material on the Big Quiz, as well as all material covered since
then and all material discussed in class since the start of the course, has
the potential of being included. Bring a calculator. An ASCII table will be
provided at the beginning of the test, and after the test begins, you can put
any additional scratch work on your ASCII sheet that you wish (a
hex-binary-decimal table, for example).
Note: An answer key for the Big Quiz is now
available.
|
|
|
F 10/18/13
|
No additional HW due. An
educational video will be shown.
|
|
|
M 10/21/13
|
HW due: Make a clean writeup of questions #4 and 5 (see below), which were corrupted
by typographical errors on Thursday’s test. Ms. Dunn instructed you to “do
your best,” which means that your score for those problems on the test will
be based on the quality of the explanation you gave for why you could not
answer the questions. But now, for HW, you need to do both problems for real.
Here are the corrected versions:
4. In a signed “word” format, how can you tell that 0xFFCF denotes a
negative integer?
______________________________________________________
What base-10 integer is represented by 0xFFCF? ____________ Show all work
below. Be clear, and write neatly! Minor errors will be forgiven.
5. For the word value given in #4, give (in both decimal and hex) the
integer that is 1 greater.
Decimal answer: ______________________
Hex answer in word format: ______________________
|
|
|
T 10/22/13
|
No class. However, extra
help for tomorrow’s HW assignment will be available in MH-102 during the
usual class time, 9:50-10:40 a.m.
|
|
|
W 10/23/13
|
HW due:
1. Subtract the “word” integer 0xFD30 from 0xF1A6. Show all work, along with
a sentence of explanation here and there. For example, if you compute the
twos complement at some point, say, “We now compute the twos complement,
namely _______ + 1 = _______ .” Give answer in hex.
2. Convert 0xFD30, 0xF1A6, and your answer from #1 into decimal (base 10).
Show work.
3. Verify that your answer to #1 is correct by using the values in #2 to
perform ordinary subtraction. In other words, show that your decimal equivalent
for 0xF1A6, minus your decimal equivalent for 0xFD30, equals your decimal
equivalent for the answer to #1.
4. Add the dword integers 0x7382ABCD and
0x480B2FEA. Show work, and circle your answer (in hex). Is something fishy
about your answer? Explain why this should be reported as “overflow” if you
were a firmware programmer.
5. Add the dword integers 0xFFFFFFEA and
0x80000012. Show work, and circle your answer (in hex). Is something fishy
about your answer? Explain why this should be reported as “overflow” if you
were a firmware programmer.
6. Convert each of the following power ratios to dB. The first 2 are done for
you as examples. “W” means watts. You may have to look up some of the
prefixes online.
Input: 100 mW. Output: 300 W. Output ratio = 3000:1
= +35 dB
Input: 600 KW. Output: 3 W (microwatts). Output ratio = 1:200 billion = –113
dB W (microwatts). Output ratio = 1:200 billion = –113
dB
Input: 10 W. Output: 2 W. Output ratio = ______________ = _______
Input: 1 W. Output: 400 MW. Output ratio = ______________ = _______
Input: 0.001 mW. Output: 600 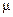 W. Output ratio = ______________ = _______ W. Output ratio = ______________ = _______
Input: 50 nW. Output. 50 mW.
Output ratio = ______________ = _______
Input: 650 W. Output: 2600 W. Output ratio = ______________ = _______
7. Convert each of the following dB gains (positive) or attenuations
(negative) to power ratios. The first 2 are done for you as examples.
+75 dB = 7 orders of magnitude up and a tripling = 30,000,000 : 1
ratio
–19 dB = 1 order of magnitude down and 3 halvings
= 1: 80 ratio
+30 dB = ____________________________ = ______ : ______ ratio
–30 dB = ____________________________ = ______ : ______ ratio
–6 dB = ____________________________ = ______ : ______ ratio
+27 dB = ____________________________ = ______ : ______ ratio
–25 dB = ____________________________ = ______ : ______ ratio
8. Convert each of the dB values in #6 and #7 to dBV.
(This is supposed to be easy.)
9. Compute the signal-to-noise ratio (SNR or S/R ratio) related to
quantization noise for each of the following digital audio formats. Be sure
to specify the proper units for your answer in each case.
(a) 10 bits per sample: _________________________
(b) 16 bits per sample: _________________________
(c) 32 bits per sample: _________________________
|
|
|
Th
10/24/13
|
HW due:
1. Complete yesterday’s assignment for correctness
as well as neatness. Neat cross-outs (single large “X”) are permitted, but scratchouts and scribble-outs are not. Use pencil. Comparing answers with
others is permitted, as long as you do not copy answers. Do not bypass the
“understanding” step!
Note: For full credit, you must
follow the formatting requirements shown here.
2. Subtract 0x1499BCAB71E84FCA from 0x67EDFDCBE951BE44. Show all steps. Give
answer in both hex and ASCII text (interpreted using big-endian format). Warning: Do not even attempt to
convert to base 10. You may blow your calculator’s mind if you try.
Note: The original version of this
problem contained a typo. The subtrahend is 0x1499BCAB71E84FCA (correct), not
0x1499ACAB71E84FCA (incorrect).
|
|
|
F 10/25/13
|
HW due:
1. Get some sleep.
2. If you did not do #2 in yesterday’s assignment by adding the complement of
0x1499BCAB71E84FCA, then do it over from the beginning. Neatness counts. This
should not take too long. Be sure to distinguish lower and upper case.
2A. If you did not achieve the message “STA winz”
in yesterday’s question #2, then find your mistakes and correct them. There
will be no partial credit today for a wrong answer. Correctness is required,
regardless of whether or not you used the correct “adding the complement”
method previously.
3. Convert each of the following input power levels to the appropriate output
power level. The first two are done for you as examples.
2 mW, +49 dB gain: up 4 orders of magnitude with
3 doublings = 80,000:1 ratio 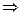 160 W 160 W
500 KW, –30 dB attenuation: down 3 orders of magnitude = 1:1000
ratio 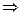 500 W 500 W
0.01 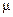 W, +95 dB gain: ______________________ = ____________ ratio W, +95 dB gain: ______________________ = ____________ ratio
 _____ _____
1750 nW, +130 dB gain: ______________________ =
____________ ratio  _____ _____
500 mW, –65 dB attenuation: ______________________
= ____________ ratio  _____ _____
880 MW, –53 dB attenuation: ______________________ = ____________ ratio  _____ _____
70 W, +57 dB gain: ______________________ = ____________ ratio  _____ _____
56 W, –56 dB attenuation: ______________________ = ____________ ratio  _____ _____
|
|
|
M 10/28/13
|
HW due: Write the exercise
below.
Creative Exercise.
The purpose of this exercise is to make decibel measurements more personally
meaningful to you. For example, we all know that a dollar is bigger than a
quarter, but how much bigger? Answer: +6 dB, since we must double twice to go
from a quarter to a dollar. Another example is that the power rating of some
large PA speakers (say, 300 W) might be 100 times the power of the speakers
attached to your computer (say, 3 W). That’s a ratio of +20 dB.
Give an example from real life of each
of the following. You may not use the same category of example more than
once. That means, for example, that if you use money for one answer, you
have to find other illustrative examples for all the others. The first one is
done for you as an example.
+7 dB: Mr. Hansen is 51, and his nephew is about 11½. That is a factor of
almost 5, which means that Mr. Hansen’s age is approximately 7 dB up.
+46 dB: ________________________________________________________________
–3 dB (“3 dB down”): ______________________________________________________
+90 dB: _________________________________________________________________
–55 dB: _________________________________________________________________
–10 dB: _________________________________________________________________
–38 dB: _________________________________________________________________
–18 dB: _________________________________________________________________
+26 dB: _________________________________________________________________
|
|
|
T 10/29/13
|
No class. However, extra
help will be available in MH-102 during C period for anyone who needs it.
Here, to help you study, is Mr. Hansen’s take on the rest of the “Creative
Exercise” HW assignment that was due yesterday:
+46 dB = up 4 orders of magnitude and 2 doublings = 40,000:1 ratio
That’s like the difference between a 1-liter bottle of
Gatorade (approximately 2 lbs.) and a fully loaded semitrailer truck (80,000
lbs.). The semi’s weight is 46 dB up.
–3 dB (“3 dB down”) = half as big = 1:2 ratio
Say you were earning $90,000 a year, which is a good salary
(even in Washington), and suddenly your boss announces that you must accept a
3 dB pay cut. Ouch! That would make your salary only $45,000 a year. You
could survive on that, but you wouldn’t be able to live in an expensive
apartment or drive a fancy car, that’s for sure.
+90 dB = up 9 orders of magnitude = 1 billion:1 ratio
This is a huge difference. The distance from the North Pole
to any point on the equator is approximately 10,000 km, which is 10 million
meters or 1 billion centimeters. Therefore, going up 90 dB is like expanding
from 1 cm (about the size of a fingernail) to a quarter of the distance
around the world.
–55 dB = down 5 orders of magnitude and dividing by 3 = 1:300,000 ratio
Light travels at a speed of about 300,000 km per second.
Slow that way, way, way down to 1 km per second, and you still have a
fast-moving object, faster than any jet plane! Or, think of taking a baseball
stadium lit up with high-intensity lights (300 KW) for a night game and
replacing them with a feeble 1-watt light, which would be fainter than a
small candle. That’s what 55 dB down would mean.
–10 dB = easy, since “10 equals 10”
Taking something down 10 dB means dividing by 10. Take a
10-foot-high basketball rim, and lower it to a height of 1 foot. It’s much
easier to dunk the ball now, isn’t it?
–38 dB = down 3 orders of magnitude, dividing by 3 (–5 dB), and dividing
again by 2 (–3 dB)
The original has to be reduced by a factor of 6000. A house
with 6000 feet of floor space would be an enormous mansion, larger than the
vast majority of houses in the Washington area. Reducing such a house’s
square footage by a factor of 6000 would produce something with about as much
floor space as a doll’s house.
–18 dB = similar to last question, except down by a less dramatic factor (60
instead of 6000)
Since –18 dB is 20 dB up
from –38 dB, we can do what we did before with –38 dB (namely, reduce by a
factor of 6000) except with 2 fewer orders of magnitude. That means reducing
by a factor of 60 instead of by a factor of 6000. Think of shortening a
commercial from 60 seconds down to 1 second, or shortening a 50-minute class
down to less than a minute.
+26 dB = up 2 orders of magnitude and 2 doublings = 400:1 ratio
Pinching someone with a pressure of 100 pounds per square
inch would probably not even make a bruise, as long as the pressure didn’t
continue for a long period of time. However, pinching someone with a pressure
26 dB up from that, 40,000 pounds per square inch, would cause permanent
injury or fatality. Human fingers couldn’t pinch that strongly, of course,
but a fictional steel cyborg (Terminator?) could manage 40,000 pounds per
square inch.
|
|
|
W 10/30/13
|
Test (100 pts.) on all material since the beginning
of the year. The material will be
similar to what you saw on the practice test
(click here for answer key), plus dB and
dBV.
|
|
|
Th
10/31/13
|
No additional written HW
due.
|
|
