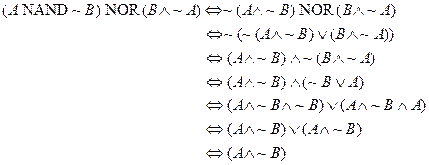|
W 9/4/13
|
First day of class.
|
|
|
Th
9/5/13
|
HW due:
1. Send Mr. Hansen an e-mail. Please use a double underscore (__) at the
beginning of your subject line. Contact information is available at
www.studyofpatterns.com.
2. If you have not already done so, order the course
textbook. Note that used copies are available for an extremely reasonable
price.
|
|
|
F 9/6/13
|
HW due:
1. Order your textbook if you have not already done so! (See link above.)
Also, if you have not already done so, send an e-mail as described in #1 of
the previous assignment. James and Ryan still need to take care of this.
Answer the remaining homework problems, in writing, using the format
specified in the HW guidelines (see link at top of schedule). This assignment
will be collected.
2. Translate each of the following binary numbers into base 10:
0100
1010
1011
10110
000110011
3. Translate each of the following base-10 numbers into binary:
10
17
33
15
12
1
5
4. Can the integer 256 be represented by a single byte of storage? Why or why
not? Explain your reasoning using a few complete sentences. (Capitalize the
beginning of each sentence, and end each sentence with a period. Use good
grammar and punctuation.)
|
|
|
M 9/9/13
|
HW due:
1. James still needs to send an e-mail! (See #1 in the entry for Thursday,
9/5.)
2. Call a classmate and compare answers for the assignment due last Friday.
Make sure that you not only agree on the answers but can explain the correctness of each answer.
In class: Possible oral quiz to verify that you understand all the answers
from last Friday’s HW assignment.
|
|
|
T 9/10/13
|
No class.
|
|
|
W 9/11/13
|
HW due: Read the material below, and do the
exercises. You may use the Windows calculator (Calc.exe) to check your
answers, but you must show your work neatly for full credit. Wrong answers
with good work showing understanding are worth more than correct answers with
inadequate work. Write your assignment on a sheet of paper, following these formatting guidelines.
When we perform addition in base 10, we carry
from each column of a certain place value into the next column. For example,
when we add
367
+858
we have 15 in the ones’ column, which we write down as 5 with a “carry” of 1
into the tens’ column. We then add 1+6+5 to get 12, which we write down as 2
with a “carry” of 1 into the hundreds’ column. Finally, we add 1+3+8 = 12,
which we write down as 12. Final answer: 1225.
Hex addition follows exactly the same rules, except that we “carry” after
passing 16, not 10. Also, we must remember to write down all our intermediate
results in hex. Here is an example:
0xFACE
+0x FAB
We start in the rightmost column with E+B, which is 25 (in our usual base 10
numbering system), but we can’t write it as 25. Instead, we think of it as 1
group of 16 with 9 left over, which is 0x19. So, we write down the 9
underneath the E and B, and we “carry” the 1.
Next, 1+C+A would be 23 (in base 10), but that’s 0x17. Therefore, we write
the 7 underneath the C and A, and we “carry” the 1 to the next column.
Next 1+A+F would be 26 (in base 10), but that’s 0x1A. Therefore, we write the
A underneath the A and F, and we “carry” the 1 to the final column.
Finally, 1+F can be thought of as 1+15 (in base 10). Well, what is 1+15? The
answer is 16, but we can’t write 16.
As always, we must write the answer in hex, as 1 group of 16 with 0 left
over, or 0x10.
Final answer: 0x10A79. You can easily verify that by using the Windows
Calculator in “Programmer” view.
Here is how you would show your work, including the carries:
111
0x FACE
+0x FAB
0x10A79
If you have any questions, please reread the example, working carefully with
pencil and paper. If you still have problems, call a classmate or Mr. Hansen
(see contact information under link at www.modd.net).
When you understand what you’re doing, perform each of the following hex
additions:
1.
0x32
+0x18
Be careful! The answer is not 50!
2.
0xC00C
+0xB00C
3.
0xABCDEF
+0x111111
4.
0x303034C
+0x2188ACF
5.
0xDEF
+0xCAB
Remember to follow the formatting guidelines as
you write up your assignment.
|
|
|
Th
9/12/13
|
HW due:
1. Read this paragraph:
Dear Student,
Twos complement arithmetic is not easy. However, it is not so bad once you
get the hang of it. The key thing to keep in mind is that these rules were
developed to make things super-easy for computers to execute, not for us.
Computers can perform a twos-complement operation in a few nanoseconds: All
they have to do is flip the bits and add 1. Sure, it takes us a little
longer, but that’s because we’re wired as humans, not as computers. If you
make an occasional mistake, that’s perfectly OK—as long as you show your work
and make a sincere attempt to understand the concepts.
Best wishes,
Mr. Hansen
2. Use “hundreds complement” arithmetic to perform each of the following
computations in decimal (base 10). Be sure to show your work!
(a) 44 – 15
(b) –38 – 3
(c) 31 + 43 (Warning! This is a
trick question. Try to explain why.)
(d) –27 + 43
(e) 37 – 48
3. Translate each entire problem
into base 10, showing your work. Then, use “twos complement” arithmetic to
perform the indicated computation in hex (base 16). Remember, the way we find
the twos complement of any number is to flip the bits and add 1. (That is the
same as subtracting from 0xFF and then adding 1 at the end, or subtracting
from 0x100 and not adding 1 at the
end.) The first two are done for you as examples that you can copy into your
homework paper. You do need to do them, though.
(a) 38h – 1Dh
(b) –0x52 – 0x28
(c) 0x39 + 0x38
(d) 5Ch – 6Fh
(a) Solution: 38h = 3(16) + 8(1) =
56, and 1Dh = 1(16) + 13(1) = 29. Since 56 – 29 = 27, the answer we
eventually get in hex should equate to 27. Since we can’t subtract, we
must re-encode 1Dh as its twos complement. If we flip the bits (same as subtracting
from FFh, but computers don’t subtract—they simply
flip the bits), we get E2h. We must then add 1 (don’t forget!) to get E3h as the twos complement of 1Dh.
Now we add:
0x38
+0xE3
0x11B
The leftmost hex digit (of 1) is a carry, which is discarded in recognition
of the fact that our “twos complement” was 100h higher than the true value.
Final answer: 1Bh, which equals 1(16) + 11(1) = 27. Hurray!
(b) Solution: 52h = 5(16) + 2(1) =
82 and 28h = 2(16) + 8(1) = 40. Since –82 – 40 = –122, the answer we
eventually get in hex should equate to –122.
In order to record the “negative” of 0x52, we must take the twos complement.
So, let’s flip the bits to get 0xAD, and add 1 to get 0xAE.
In order to subtract 0x28, we must again take the twos complement. So, let’s
flip the bits to get 0xD7, and add 1 to get 0xD8.
Now we add:
1
0xAE
+0xD8
0x186
So our answer is 0x186, right? No, not
so fast. The second carry of 1 must be discarded in recognition of the
fact that we are working in twos complement arithmetic.
So our answer is 0x86, right? No, not so fast! Our lead digit is 8 or greater, which means that
the answer must be interpreted as a negative number. What negative number,
you ask? Why, the negative number found by taking the twos complement of 0x86.
Flip the bits to get 0x79.
Now add 1 to get 0x7A. We remember the fact that our answer is negative, and
since the value of 0x7A is 7(16) + 10(1) = 112 + 10 = 122, our final answer
is –122. Hooray!
|
|
|
F 9/13/13
|
HW due:
1. Add FFFF to each of the following dword
integers. Use the trick we learned in class, so that if you are given a
similar problem in class, you can answer it instantly!
(a) 0xAE45312C
(b) 0xFACEB00C
(c) 0xF00F00BA
(d) 0xC0C0BABB
2. Write the number –20 in
(a) byte format
(b) word format
(c) dword format
(d) qword format
3. (a) Be creative! Make up a dword subtraction
problem that is unique to you. Write it up with a combination of text and
diagrams, so that it is clear that you know what you’re doing. Describe the
steps as if you were speaking to a reader who is smart enough to understand
plain English but who has no technical skills. For example, you have to
assume that your reader doesn’t know what is meant by “taking the twos
complement.” You’re actually going to have to explain how to take the twos
complement.
(b) Showing your work, verify that your subtraction problem in part (a) is
correct by redoing it in base 10.
Note: For #3(a), if you are not a
good writer, you may prefer to make a video. A video will be accepted for full
credit. One site that provides good tools for making educational videos is
Educreations.com, and it is free. However, you can use another app or another
site if you wish.
|
|
|
M 9/16/13
|
Every year, there is a one fall weekend with
weather so perfect, so ideally suited for outdoor activities, that it would
be a crime to have any homework due. This is it! Enjoy your weekend of no
additional homework, and get some good sleep. If you are behind on your
homework, this is your chance to catch up.
|
|
|
T 9/17/13
|
No class.
|
|
|
W 9/18/13
|
HW due: Read the paragraphs below, and then write
the indicated problems. Show your work!
So far, we have seen how binary storage (notated in hex, which is a more
convenient notation) can be used to represent integers in twos complement format—whether
as byte format, as word format, as dword format, or
as qword format.
Binary storage can also be used to represent floating-point numbers (i.e.,
fractions or “decimals”—non-integers, in other words). The details are a bit
complicated, but we will learn how to do this at a future time.
Binary storage can also be used to represent digital audio, digital video,
still photographs, and text. Text is what we will focus on right now.
The most common representation of text uses the American Standard Code for
Information Interchange (ASCII, pronounced “ask-ee”).
Yes, the phonetic pronunciation could be spelled slightly differently, but we
won’t go there!
Click here to see an ASCII table. Do
you see that the capital letters A through Z (shown in red in the table) are
represented by hex values 0x41 through 0x5A? Please say yes!
So, here’s what we’re going to do. Instead of adding some boring old hex
values and getting boring answers, we’re going to take our answers and treat
them as if they were ASCII text, so that they spell out a secret message.
Show your work. The first one is done for you as an example.
1.
1111 1
0x48859115
+0x0ACEB00C
0x53544121
0x53 is the ASCII code for capital S
0x54 is the ASCII code for capital T
0x41 is the ASCII code for capital A
0x21 is the ASCII code for an exclamation point
Final answer: STA!
2.
0x3674B577
+0x0D00BEEE
3.
0x560E59E8
+0x18611865
4.
0x0648C1AD5A5F73F6
+0x3C2C8ABEEA0FD384
|
|
|
Th
9/19/13
|
HW due:
1. Try to solve Challenge #1 from yesterday’s
handout. If you simply can’t get it, move on. Hint: The secret message in Challenge #1 is a 6-word sentence.
2. How many gigabytes are in an exabyte?
3. A DSL modem with a download speed of 700 kbps is used to transfer a 4 GB
movie. Estimate the download time required. (Hint: kbps means “thousands of bits per second.” To convert bps
to bytes per second, you might think you should divide by 8, but actually it
is much better to divide by 10. The reason is that the transmission of
digital data always includes some “extra” bits for flow control and error
correction, and dividing the bps by 10 gives an easy and quite reasonable
estimate of the number of bytes per second.)
4. The 30-year-old laptop computer in Mr. Hansen’s classroom has a total SSD
storage capacity of 32 KB.
(a) Approximately how many of those computers would be needed to store a
terabyte of data?
(b) Approximately how many times faster is a modern computer running at a
clock speed of 3 GHz compared to Mr. Hansen’s old computer running at 2.5
MHz? (GHz means gigahertz, and MHz means megahertz.)
5. In a byte format, what integer is represented by 0xC9? Give the integer
(in both decimal and hex) that is 1 greater than that.
6. Using a dword format and twos complement hex
arithmetic, subtract 0x51ABBA3A from 0x380A30B9. Show and explain all steps.
After you have computed the final answer in hex, convert the final answer to
decimal (base 10), explaining your steps.
7. Convert the 3-byte text string STA (all capitals) into hex. Then convert
the 3-byte text string NCS (also all capitals) into hex. Then, treating both
results as if they were hex integers in dword
format, add them together. Show your work.
Optional (bonus): In #7, convert the final answer into base 10, showing your
work.
|
|
|
F 9/20/13
|
Big Quiz (70
pts.) on all material covered to date. See the study guide below as you
prepare for the assessment.
1. You should be able to perform all the computations in yesterday’s HW
assignment without too much difficulty. Occasional “slip-up” errors are
acceptable, without point penalty, as long as your work is neat and you
demonstrate that you know what you are doing. Consistently forgetting to add
1 when computing the twos complement is not
considered a slip-up, however, and you would be docked points for forgetting
to do that. Click here for the
solutions to yesterday’s HW.
2. You should know the following terms: bit, byte, hex (hexadecimal), Hertz
(cycles per second), twos complement, nybble, word,
dword, qword, carry, place value, kilobyte,
megabyte, gigabyte, terabyte, petabyte, exabyte,
zettabyte, yottabyte, HD, SSD, head crash, steganography, ASCII, Unicode.
Mnemonic aids (e.g., “Karl Marx gave the proletariat eleven Zeppelins, yeah!”
or “Keep my green turtle PEZ-y”) are optional.
3. You should know (cold) the fact that 210 = 1024, and you should
be able to perform algebra using the fact that 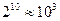 to estimate many
answers involving powers of 2. For example, approximately how many different
keys are possible if 256-bit keys are used? Solution: 2256 = (210)25.6 to estimate many
answers involving powers of 2. For example, approximately how many different
keys are possible if 256-bit keys are used? Solution: 2256 = (210)25.6
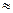 (103)25.6
= 1076.8 (103)25.6
= 1076.8 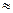 1077,
which is 1 followed by 77 zeros. Wow! That’s a lot of possibilities! The
total number of atoms in the universe is somewhere in the vicinity of 1080,
which is “only” 1000 times larger. 1077,
which is 1 followed by 77 zeros. Wow! That’s a lot of possibilities! The
total number of atoms in the universe is somewhere in the vicinity of 1080,
which is “only” 1000 times larger.
4. You should be able to perform ASCII table lookups if you are furnished
with an ASCII table.
5. Rule of thumb: Divide bits per second (bps) by 10 to estimate the usable
bytes per second.
6. You should be able to reproduce “the chart” from memory: binary, decimal,
and hex representations of the 16 possible values for a nybble.
7. Explain how to detect an overflow condition when adding or subtracting in
twos complement. The rule is this: If you add 2 positive numbers and get a
negative answer, or if you add 2 negative numbers and get a positive answer,
then overflow has occurred. Overflow is not
determined by having a carry out of the leftmost hex digit, since that carry
is simply ignored when we are doing twos complement arithmetic.
8. You should know what the following abbreviations stand for: ASCII
(American Standard Code for Information Interchange), K, M, G, T, P, E, Z, Y,
B (byte), b (bit), ps (per second), Hz (Hertz, or
cycles per second), 0x, and h. Note that 0x is a prefix and h is a suffix,
both of which indicate “hex,” but you would never use both with the same
number.
|
|
|
M 9/23/13
|
HW due: Print out last
Friday’s big quiz, and correct the entire test including all of #10 to a
100% level of perfection. Redoing “the chart” (binary/decimal/hex) is not
necessary unless you want to have an extra one for reference, since everyone
did OK on that part of the test. Collaboration with other students is
permitted, but only if you describe for
each problem the exact concept that they helped you with. See examples
below.
Acceptable: On
#10, Joey reminded me to add 1when taking the twos complement, and Freddie
helped me find an exponent error in my conversion back to base 10.
Unacceptable: Joey
and Freddie helped me find errors in my arithmetic.
If there are any problems you are certain you answered correctly on the test,
you may omit them when writing up your corrections.
Neatness counts! Accuracy also counts, since you have enough time to double-check
your answers. You must show your steps clearly. Use a calculator, please, but
remember to use standard notation, not calculator notation. For example, 2.36E72 is not acceptable; you should write 2.36
· 1072 instead.
Your score on your corrections will be used to improve your test score.
Everyone needs to do this!
First, the good news: Everyone’s binary/decimal/hex chart looked OK. (Well,
several students still don’t know how to write the number 4, but hopefully
they’ll fix that in the corrections!)
Now, for the scary news: Out of 13 students, only 3 had a correct answer to
#1, believe it or not, and #1 was supposed to be quite easy. Question #5 was
even easier, and only 4 people got it completely correct. There were 3 more
students who on #5 gave a correct answer without commas, which is a small
deduction for readability, but that still leaves 6 people with answers that
were completely wrong. Hmmm, it’s supposed to be a gift . . . G means
billion, and Hz means cycles per second, so . . . cough, cough, and it’s not
even a power of 2, either, since frequency doesn’t rely on binary arithmetic.
Now, everyone understands that the first big assessment of the year is
stressful. That’s why you’re getting an opportunity to earn some of your lost
points back. Please organize your work and write legibly. Let’s all do a good
job, OK?
|
|
|
T 9/24/13
|
No class. However, please stop by between 9:50 and
10:40 for a mini-conference on your corrections.
|
|
|
W 9/25/13
|
No additional HW due today. Your test corrections
should be approved (or, in some cases, reapproved) before the start of class.
Correct answers are expected, since you have had ample time to work on this.
|
|
|
Th
9/26/13
|
HW due:
The NOR gate (“not-OR”) is the
negation of a regular OR gate,
just as a NAND gate is
the negation of a regular AND gate.
The symbol for the NOR gate
is found here,
and we use the MIL/ANSI version of the symbol.
(a) Give the truth table for the NOR operation. Try to do this without
looking at an online reference. If you have to peek, that’s OK, but try to
answer this question without peeking.
(b) Combine NOR gates (nothing but NORs, that is) in order to create a “black
box” with 2 inputs and 1 output, so that the black box works exactly like a
standard AND gate. If you fail in this mission, you need to show several
attempts and the truth tables that prove that you failed. If you succeed, you
need to show the truth table that proves you succeeded.
Note: We learn more from our
failures than from our successes. Students who fail in part (b), or who fail
before eventually succeeding, will be much better educated than those who
look up the solution online and have the right answer from the start.
|
|
|
F 9/27/13
|
No additional HW due today, but please start
working on Monday’s assignment. It is challenging, and you may need the extra
time. Call or e-mail if you need help! Don’t wallow in a state of confusion!
|
|
|
M 9/30/13
|
HW due: Read the material below, and then do the 3
numbered exercises.
Recall that our basic operations (AND, OR, and NOT) can be denoted by the
symbols 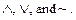 (Some sources, such
as Wikipedia, use (Some sources, such
as Wikipedia, use 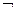 instead of ~ to
indicate NOT.) instead of ~ to
indicate NOT.)
The double-headed arrow (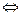 ) means “is equivalent to” and is sometimes abbreviated
EQU. Fun fact: The EQU operator is the negation of the XOR operator. ) means “is equivalent to” and is sometimes abbreviated
EQU. Fun fact: The EQU operator is the negation of the XOR operator.
The implication operator (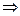 ) is defined as follows: Whenever we see ) is defined as follows: Whenever we see 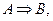 we will usually
write we will usually
write 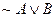 instead. For
example, instead. For
example, 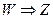 coould
be rewritten as coould
be rewritten as 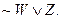
Here is a harder example: 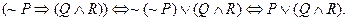
Some useful rules:
AND distributes over OR, just as multiplication distributes over
addition.
Example: 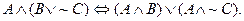
Unlike in “real” algebra, OR distributes over AND, too!
Example: 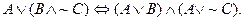
You can also “foil” mixed expressions involving ANDs and ORs in
some cases.
Example: 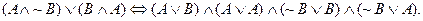
The NOT of an OR is the AND of the NOTs.
Example: 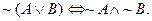
Another example: 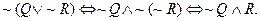
The NOT of an AND is the AND of the ORs.
Example: 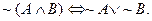
Another example: 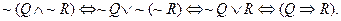
HW assignment: For
each of the following (including #1), produce
(a) a circuit diagram that implements the full logic, using all the
components mentioned
(b) a simplified Boolean algebra expression (show your work)
(c) a simplified circuit diagram that takes advantage of your simplification
in part (b)
(d) a truth table that proves that (a) and (c) are equivalent
Note that although #1 is done for you as an example, you should still redo it
in your notes, neatly.
1. Input: A, B
Output: W,
defined by 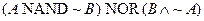
(a)
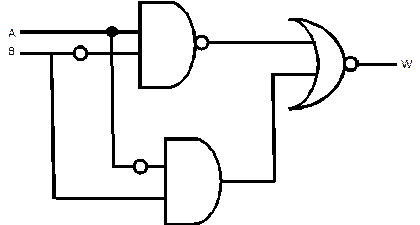
(b)
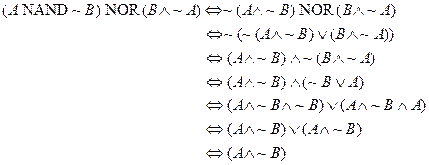
(c)
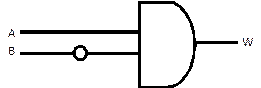
There! That’s a lot simpler, isn’t it?
(d)

2. Input: A, B
Output: W,
defined by 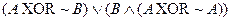
3. Input: A, B, C
Output: W,
defined by 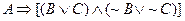
Hint: Use an XOR
gate.
 These are challenging. If you can do either
#2 or #3 without help, then please help a classmate! That way, you’ll both
learn more. These are challenging. If you can do either
#2 or #3 without help, then please help a classmate! That way, you’ll both
learn more.
|
|