|
M 1/13/14
|
Midterm Exam, MH-108, 11:00 a.m.Ė1:00 p.m.
Bring several sharpened pencils, spare batteries, and at least one standard
handheld calculator. No cell phones, handheld computers, notes, or PDAs are
permitted.
Format of the exam will be similar
to the 1-hour tests you have previously taken. However, you will have the
full 2 hours to work on it if you wish. The exam will not be comprehensive.
We will leave out many, many topic areas that we studied: twos complement,
hex addition and subtraction, data compression (lossy
and lossless), digital audio, RGB encoding, digital video, the meaning of the
acronym ďASCII,Ē aliasing, Nyquistís Theorem,
signal-to-noise ratio, dBV, Unicode, bluescreen logic (p. 243 in your textbook), information
theory, and entropy, to name but a few. Instead, the exam will focus on the
following topic areas:
1. Bits, bytes, hex, and Hertz.
- During the
first 5 minutes of the exam, you will be asked to recreate The Chart (binary,
hex, decimal).
- You may use The Chart throughout the exam, as well as an
ASCII table you will be given.
- K, M, G, T, P, and E (kilo, mega, giga,
tera, peta, exa: Keep My Green Turtle Partying Expertly?)
- K = 210 or about a thousand
- M = 220 or about a million
- G = 230 or about a billion
- T = 240 or about a trillion
- Etc.
- Hz = cycles per second
- Prefixes K, M, G, T, etc. are interpreted as powers of 10 (not powers of 2) when
used with Hz
- Computations involving powers of 2 and powers of 10
- Standard facts: 8 bits in a byte, 210 = 1024 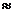 †103 †103
- On every single test: Number of patterns possible with n bits = 2n, and you must
know this to pass the class!
- Given the size of a key, estimate the size of the keyspace.
-- Example:
256-bit key provides 2256 = (210)25.6 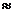 (103)25.6 (103)25.6 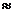 †1076.8 †1076.8 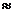 †1077
possibilities. †1077
possibilities.
- Rule of thumb: Divide bits per second (transmission speed)
by 10 to estimate bytes per second.
-- Therefore, 150
kbps becomes 15 KB/sec., 700 mbps becomes 70 MB/sec., etc.
- Terminology: word, dword,
qword, binary, hex, nybble, KHz, MHz, GHz,
little-endian, big-endian
- Given a bitstream in binary, be
able to convert to hex (big-endian) and then to hex (little-endian).
- Mooreís Law: Computing power at a given price level
doubles approximately every 2 years.
2. Decibels.
- Convert from a ratio to dB. For example, 5000:1 = +37 dB,
and 1:200 = Ė23 dB.
- Convert from dB to a ratio. For example, Ė100 dB =
1:10,000,000,000, and +56 dB = 400,000:1.
- Given an input power level, use dB to convert to output
power level. Example: 5 mW + 40 dB = 50 W.
3. Digital Logic.
- There is so much we could do here! But time is limited,
so we will use our imagination.
- You will be given a collection of AND, OR, NOT, XOR,
NAND, and NOR gates with only 2 inputs (A and B).
- Your job is to simplify the circuit. Be sure you can
recognize symbols for AND, OR, NOT, XOR, NAND, NOR.
- You may do this by pretending that the circuit has been
encoded in Michaelís Minecraft world (optional).
- Trace through and see what happens when A and B are both
1, when A is 1 and B is 0, when A is 0 and B is 1, etc.
- From that, you should be able to recognize the output
pattern and write a simplified circuit diagram.
4. Error Detection
- Since we donít have time to do error correction, weíll
settle for error detection.
- You will be given several bytes of data and asked to
identify which byte(s) might contain bit errors.
- The protocol will be even parity, with the 8th bit
reserved for parity.
- Terminology: parity, error detection, error correction,
protocol
5. Other Terminology.
- The projects brought many terms to light:
cryptographic hash functions, QR codes, PSK, AES, PGP, etc., etc.
- However, the only project-related term that will be
tested on the exam is non-repudiation.
- You can look that up on Wikipedia, or you can remember the
short working definition: Non-repudiation
means that a system provides sufficient controls so that a validated author
of a message or file cannot plausibly claim later that he didnít produce it.
In other words, non-repudiation rules out the Bart Simpson defense (ďI didnít
do it. Nobody saw me do it. You canít prove anything!Ē).
6. PRNG applied to PKI, with XOR
encryption/decryption.
- Needless to say, you must be able to define the terms
PRNG, PKI, and XOR.
- You will be given a private key (I) on a slip of paper.
- Parameters C, A, B,
and N will be provided and will be
the same for everyone.
- Compute your public key, P = CI mod N. If you do it correctly, Mr. Hansen
will write it on the board.
-- Note: If you make a mistake, Mr. Hansen
will correct it so that other people arenít messed up later.
- A fake secret 24-byte message from someone else in the
class will be given to you (in hex).
- Let Q represent
that personís public key. If he computed it incorrectly, Mr. Hansen will
correct it for you.
- Compute the shared secret, QI mod N,
and call that value X(0), the seed
for your PRNG.
- Compute X(1)
through X(24), the first 24 outputs
from your PRNG. Formula is X(k + 1) = AX(k) + B mod N.
- Convert those 24 outputs to hex. (If you do the first 2
correctly, Mr. Hansen will give you the remaining ones.)
- XOR the 24 bytes of the secret message with the 24
outputs from your PRNG.
- Translate the result using your ASCII table, and youíre
finished!
In topic area 6, which will take most of your time, you will be given the
steps listed above but not the formulas. Small hints may be provided if you
get stuck in the middle, since everyone needs to translate the secret
message!
If you forget the formulas used in topic area 6, you can purchase hints for a
small point fee. The following are the three formulas you should memorize:
Your public key = P = CI mod N.
Shared secret = QI mod N, where Q = other personís public key, I = your own private key.
The next output of a PRNG, X(k + 1), equals AX(k) + B mod N. In other words, to get the next
output, you must multiply the previous output by A, add B, and take the
result mod N.
If time permits, a few more sample questions and answers may be posted here
on Sunday, Jan. 12.
Here is a sample problem for topic area 3 (digital logic):
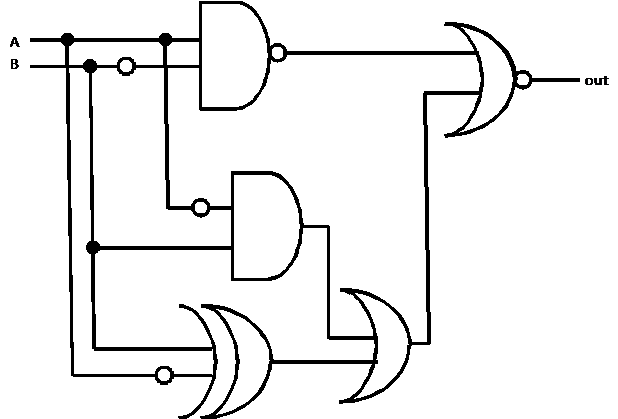
Solution
By patiently tracing through the diagram, we obtain this truth table:

Note:
Be sure to show your work, since otherwise there will be no way to give
you partial credit if you make a mistake.
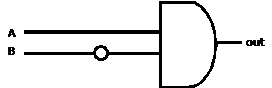
The output is true if and only if A is true and B is false. The simplified
logic is therefore 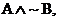 †shown by this vastly
less cluttered circuit diagram: †shown by this vastly
less cluttered circuit diagram:
Alternate Solution (optional)
The original diagram can be written out as 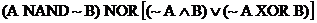 . .
After about 7 or 8 tricky steps with Boolean algebra, you can prove that the
expression simplifies to 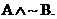 †Thatís a useful
skill, but it wonít be tested on the exam. †Thatís a useful
skill, but it wonít be tested on the exam.
Another Sample Problem for Digital
Logic
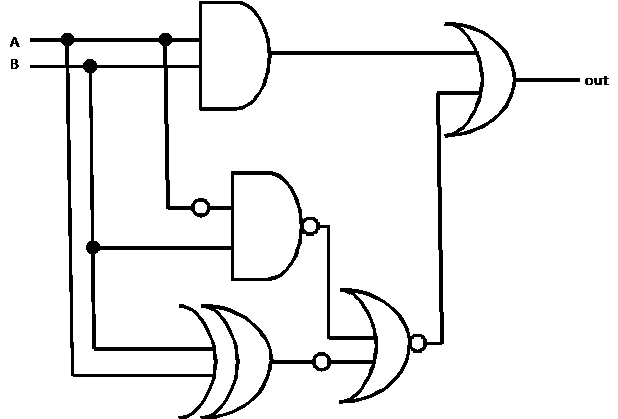
Solution
Again, take your time and trace through the diagram for all 4
possibilities (A and B both 1, A true and B false, A false and B true, A and
B both 0). You should eventually obtain this truth table:

The output pattern looks familiar. Itís the same pattern as B, in fact. The A
input plays no role. Therefore, we can really
simplify the logic. Here is the simplified diagram:

|
|





