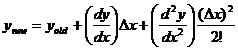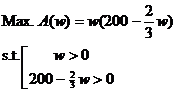|
F 11/1/13
|
Last day of Q1.
HW due:
1. Read §§6-5 and 6-6.
2. Prove §6-4 #1 (OK to use proof on p. 266 as a guide).
3. Prepare §6-5 #1-18 all for oral presentation.
4. Write §6-5 #19-23 odd, 38.
5. Prepare §6-6 #5-12 all for oral presentation.
6. Write §6-6 #21.
|
|
|
M 11/4/13
|
HW due: Finish the
assignment that was due Friday. Because of Homecoming weekend, there is no additional
assignment, but you are expected to spend an additional 35 minutes if
necessary.
|
|
|
T 11/5/13
|
No additional written HW
due. Please make sure that you are fully caught up on old assignments.
|
|
|
W 11/6/13
|
HW due:
1. Read §§6-7 and 6-8.
2. Prepare §6-7 #1-36 and 41-52 for oral presentation. If any of these
require more than a moment’s thought, make a note in the margin of your
textbook so that you are ready to present if called upon.
3. Write §6-7 #56, 58. For #58, note that the integrand is 2 cosh x;
therefore, use the cosh function (found under 2nd
CATALOG) when performing the numeric integration with MATH 9.
4. Write §6-8 #8, 14, 20, 22, 24.
|
|
|
Th
11/7/13
|
HW due:
1. Read §6-9. Be sure to memorize the last 2 formulas in the green box on p.
292, since you don’t want to re-derive those on the fly!
2. Prepare §6-9 #1-80 for oral presentation.
3. Write §6-8 #28-30 all, §6-9 #81-90 all.
|
|
|
F 11/8/13
|
No school (faculty meeting
day).
|
|
|
M 11/11/13
|
HW due:
1. Read §§7-1 and 7-2.
2. Write §7-1 #1-6 all, especially #6.
3. Write §7-2 #5, 8.
4. (Optional.) Write §7-2 #9.
|
|
|
T 11/12/13
|
HW due: Read §7-3; write
§7-3 #3, 4.
|
|
|
W 11/13/13
|
HW due: Read §7-4; write
§7-3 #10, §7-4 #2. If you have not already completed §7-3 #4, then use the
answers read in class yesterday to do so (required).
|
|
|
Th
11/14/13
|
HW due: Read §7-5; write §7-4
#4abcd (see part (d) below), 8abcde. For #4ab and #8bde, you may make your
sketches in pencil directly in your
textbook if you prefer not to make a photocopy.
#4(d): Use an analytic process to derive the exact solution described in part
(c). Hint: Consider the second
derivative.
|
|
|
F 11/15/13
|
IMPORTANT: Do not enter MH-102 during the
CyberPatriot competition. Today’s class will be held in Sam’s Bar.
HW due:
1. For the diff. eq. given in class yesterday, namely 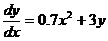 with initial
condition (1, 4), with initial
condition (1, 4),
estimate y when x = 2.5. Use a step size of 0.5. Note: Show the entire set of column
labels and work, even the portions that were done for you in class yesterday.
2. Show that a step size of 0.125 in #1 gives a dramatically different
result. Feel free to use a spreadsheet or a computer program, but show the
same columns as in #1.
3. Write §7-5 #2, 3abc. Try to write the calculator program in #2 by
yourself, but if you simply can’t do it (or don’t know enough about
calculator programming to try), then you can adapt this program for your purposes.
|
|
|
M 11/18/13
|
HW due:
1. Read §8-2. Note that we are skipping §7-6.
2. Get caught up on all previously assigned written work, especially §7-4 #4d
(see problem in 11/14 calendar entry).
3. Use a second-order method as
follows to redo Friday’s problems #1 and #2. In other words, use the same diffeq. with step sizes of 0.5 and 0.125, but with the
following method that is more sophisticated than Euler’s method:
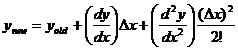
That is, you will add another term that utilizes second-derivative
information (concavity) at the latest point (x, y). That way, the
estimated solution track should have some built-in parabolic curvature
instead of following nothing but stubby line segments.
4. Make a detailed sketch of the slope field for x values between 1.0 and 2.5. Which method, the Euler approach
from last Friday or the second-order method you used a moment ago, seems to
work better? What is the role of step size?
|
|
|
T 11/19/13
|
HW due:
1. Repeat problems 3 and 4 from last Friday. Now that the typo has been
corrected, you should get much better results! Sorry for the mistake.
2. Prepare §8-2 #1-12 for oral presentation.
3. Write §8-2 #13-19 all.
4. Read the green box at the bottom of p. 368. Make a couple of reading
notes. If possible, explain the following cartoon:

5. Answer the following questions.
(a) In general, is it more useful to look at the first derivative or at the
second derivative when trying to decide if a critical point is a local
extreme (min. or max.)? Explain.
(b) Is the origin a point of inflection for the function y = tan–1 x?
How about for the function y = x1/3? Explain each
decision.
|
|
|
W 11/20/13
|
HW due: Work the review
problems listed below. If you do not finish all of them, then keep a time log
and finish the rest for Thursday. Bring the entire set to the test on
Thursday.
p. 246 #T4abcd
p. 298 #R7bc
p. 299 #R7f, R8df, R9abc
p. 345 #T1ab
p. 346 #T3abcd
p. 430 #C2, C3
p. 431 #T1, T2
In class: Review.
|
|
|
Th
11/21/13
|
Test (100 pts.), calculator allowed throughout. Focus will be on §5-5 through §8-2, but as with all
other tests this year, there is a “cumulative spirit” to the test. Theorems
that you are expected to be able to apply and state correctly (including all
hypotheses) are FTC1/2, EVT, IVT, and MVT. Important definitions include
Riemann sum, Riemann integrability, variable-factor
product, differential equation, slope field, initial condition, solution,
critical point, point of inflection, plateau point, local extreme (min/max),
absolute (global) extreme. Formulas you are expected to have memorized by now
include the trapezoid rule, the midpoint rule, the left and right endpoint
rules, and Simpson’s Rule.
Important: Bring all of your
review problems!
Sample Problem:
Let 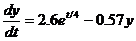 with initial
condition y(0) = 0.2. with initial
condition y(0) = 0.2.
Use Euler’s method and 3 steps of equal size in order to estimate y when t = –1.5.
Solution (inadequate):

Note that the student has given an absurd number of decimal places and
has done unnecessary work on the final line. Nevertheless, the nature of the
work is unclear. For example, how was each new y-value obtained? Not only that, but the answer, –4.209, is not
even circled or boxed.
Solution (much better):
Let 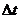 = –0.5. = –0.5.

This student has spent only slightly more time but has produced a solution
that is far clearer and more informative. Remember, do not round until the
very end. To save time, it is fine to use “. . .” to indicate that your
calculator is storing additional accuracy that you are choosing not to write
down. Be sure to state the step size
explicitly, as was done immediately above the table here! The grader
needs to see that you clearly know what you are doing and are not merely
copying numbers blindly from your calculator.
|
|
|
F 11/22/13
|
No additional written HW
due.
In class: §8-3 #1 with standard setup:
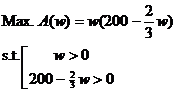
|
|
|
M 11/25/13
|
HW due: Read §8-3; write
§8-3 #7, 10, 11, 12. For each problem, be sure to set up the objective
function and constraints in the standard format specified in class Friday.
Calculus methods and calculus-style justifications are required. (For example,
you can use your calculator’s max/min finder to check your work, but not to
justify your work.)
|
|
|
T 11/26/13
|
HW due: Write §8-3 #19, 21,
22, 26. Show adequate work, including readable justifications that tie the
calculus concepts together. Use of 2nd CALC 3 or 4 (minimum or maximum
finder) is not permitted except as a check on your work.
Guest speaker, Mr. Joe Morris of MITRE
Corporation.
|
|