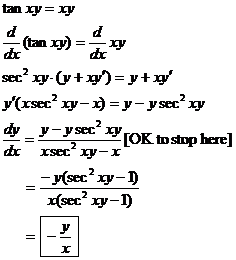|
T 10/1/13
|
HW due: Read §4-2; write
§4-2 #2, 3-21 mo3, 23, 24, 29.
|
|
|
W 10/2/13
|
HW due: Read §4-3; memorize
“ho deehigh minus high deeho,
all over ho-squared” or your favorite alternate mnemonic; write §4-3 #3-27
mo3, 28.
|
|
|
Th
10/3/13
|
HW due: Read §4-4; write
§4-4 #27-36 all, 38, 42, 43, and the problem below.
Problem.
The world’s most common function, arguably, is the table lookup, in which a
field (most frequently the record ID field, an integer) is used to “look up”
one or more other fields in a database. If City(x) returns the City field in a database of names and addresses,
then we might have City(12854) = “Philadelphia” and City(32557) = “Buffalo”
(for example). Here the domain is {integers} and the range is {text strings}.
(a) Do you think the City() function is one-to-one? Why or why not?
(b) It is also possible for a database lookup function to have as its range
objects of type “binary large object” (sometimes called BLOB). Could FavoriteMovie(12854) equal a file of several gigabytes in
size?
(c) It is more common for database tables to be “normalized,” which means
(essentially) that they do not contain long strings or BLOBs, but rather
pointers or URLs (web links) that tell where the desired object can be found.
For example, it is more realistic that City(12854) would return not the
string “Philadelphia” but rather an integer, such as 601958, that serves as a
record ID in another table, namely a table of standardized city names. In
this case, 601958 is a pointer known as a “foreign key,” because it tells how
we could find the desired information in a foreign table. Consider the
function Name(x), which returns the
text string found in the CityNames table for ID
value x. Explain why, for large
databases, using the nested function Name(City(12854)) where City(12854) =
601958 and Name(601958) = “Philadelphia”
makes more sense than using a more simpleminded approach such as
City(12854) = “Philadelphia”.
|
|
|
F 10/4/13
|
HW due: Read §4-5; write
§4-5 #10-24 all. For #13-24, use the formulas on p. 150 as shortcuts. Only
the arcsin, arcos, arctan,
and arccot formulas need to be memorized; the arcsec and arccsc derivatives
are rarely used.
|
|
|
M 10/7/13
|
HW due: Read §4-6,
including the proof on p. 154 (which must be memorized); prepare §4-6 #1-12
for oral presentation; write §4-6 #14-34 even, 38.
|
|
|
T 10/8/13
|
HW due: Read §4-7; write §4-7
#9, 10, 12. Use the extra time to finish §4-6 #38 from yesterday’s set.
|
|
|
W 10/9/13
|
HW due: Read §4-8; write
§4-8 #3-21 mo3 and 26abc. Note that #26 finishes on p. 172. The only tricky part
to these problems is that you need to be able to factor correctly. See #15
below, which is done for you as an example and should be redone exactly as
you see it here, at least to the point marked “OK to stop here.”
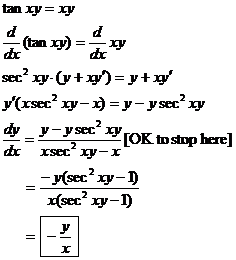
|
|
|
Th
10/10/13
|
HW due: Read §§5-2 and 5-3;
prepare §5-2 #1-16 and §5-3 #7-24 for oral presentation; write §5-2 #17, §5-3
#1-4 all.
|
|
|
F 10/11/13
|
No school (faculty
professional day).
|
|
|
M 10/14/13
|
No school (Columbus Day).
|
|
|
T 10/15/13
|
HW due: Read §5-4; prepare
§5-4 #2-32 even for oral presentation; write §5-4 #34-42 even, 43, 46.
|
|
|
W 10/16/13
|
HW due: Review problems as
listed below, plus the challenge problem.
p. 125 #R7e
p. 126 #R9 (all parts)
Use PR and CR to prove QR.
p. 173 #R3cd
p. 174 #R4 (all parts), R6cd
p. 175 #R8bc
p. 241 #R3 (all parts), R4 (all parts)
p. 242 #R6ab
p. 243 #R10ab
State EVT and IVT.
Prove that the cube root of 7 exists. It is given that all power functions
are differentiable.
Challenge Problem: Use an
appropriate u-substitution to
evaluate 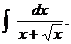
|
|
|
Th
10/17/13
|
Test (100 pts.) on almost all material from the
beginning of the year. The calculus
of formal logic will be tested, but probably only in one question. The focus
will be on §§3-8 through 5-4.
|
|
|
F 10/18/13
|
No additional HW due.
In class: Conclusion of the fractals video. You are responsible for the
contents of the video, especially the names of the key mathematicians
mentioned in the video and what they are famous for: Benoit Mandelbrot, Georg
Cantor, Helge von Koch, and Gaston Julia. If you
miss something during the video, you should find it on YouTube at home and go
over it again on your own.
|
|
|
M 10/21/13
|
No additional written HW
due. However, there will probably be a quiz or possibly 2 quizzes. You are
responsible for the contents of the fractals video. Mathematicians noted in
the video are Benoit Mandelbrot, Georg Cantor, Helge
von Koch, and Gaston Julia. If you wish to watch some portions of the video
again, it is available on YouTube. Search on keywords hidden dimension HD.
|
|
|
T 10/22/13
|
HW due: Read §§5-5 and 5-6;
write §5-5 #12, 13, §5-6 #36, and memorize the statement of the MVT (p. 203).
Rolle’s Theorem (p. 204) is of historical interest but
is less important. Pay special attention to the discussion on p. 206 about
“necessary” versus “sufficient” conditions.
|
|
|
W 10/23/13
|
HW due:
1. Skip §5-7.
2. Read §5-8.
3. Read the following paragraph.
FTC1 and FTC2 may be stated as follows. The hypothesis for each is that
function f is continuous on [a, b]
and that all dummy values of t used
below are within that interval.
FTC1: 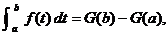 where G is any antiderivative
of f. where G is any antiderivative
of f.
FTC2: Let H(x) be an accumulator
function of f, where 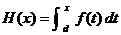 . Then . Then 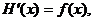 i.e., H is an antiderivative
of f. i.e., H is an antiderivative
of f.
4. Read this bidirectional proof
that FTC1 and FTC2 imply each other, and provide a reason (justification) for
each step. Do not write complete sentences; a few words will suffice in most
cases. Note: The linked page does
not provide a proof that either FTC1 or FTC2 is true. The proof of FTC1 is in
your book. The linked page merely shows that if FTC1 is true, then so is FTC2, and conversely.
5. Write §5-8 #1abc and #8abcde.
|
|
|
Th
10/24/13
|
HW due:
1. Read §§5-9 and 5-10.
2. Write §5-9 #12, 23, 24, 25, 27, 30-36 all, 38. Note: Instructions for #31-36 appear immediately below #30.
3. Prepare §5-9 #1-22 all for oral presentation where final answers are not
required. An example is given below.
Oral example for #1:
“The definite integral of x2
wrt x,
from 1 to 4, equals 4 cubed over 3 minus 1 cubed over 3.”
4. Prove the Chain Rule for Integrals, which may be stated as shown below.
CRI: Let u be a differentiable function of x, let g be a
continuous function of x, and let c be a constant. Then
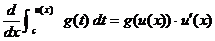 . .
5. Use FTC and/or CRI to compute each of the following. Work is optional, but
write down each starting problem (as always).
(a) 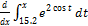
(b) 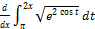
(c) 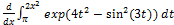
(d) 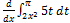
|
|
|
F 10/25/13
|
HW due: Read §5-11; write
§5-10 #3, 7, §5-11 #1, 3, and the problem below.
Problem:
Suppose that we have an even number (namely 2n) of subintervals of equal size. The trapezoid rule (pp. 19-20)
can be modified to say that if we use only the even-indexed mesh points x0, x2, x4,
. . . , x2n, then the trapezoidal sum T involving n
subintervals satisfies 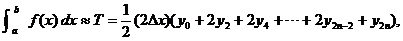
where we use agree to use yi as a shorthand notation for f (xi).
Note that we are using 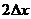 as the step size in
this context, not as the step size in
this context, not 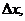 since there are only
half as many subintervals as we would normally use for mesh points x0 through x2n. since there are only
half as many subintervals as we would normally use for mesh points x0 through x2n.
Similarly, consider forming a midpoint sum using only n (not 2n) subintervals
of the same interval [a, b]. The midpoint rule (pp. 196-197)
would in this context say that the midpoint sum, M, is a Riemann sum that satisifes
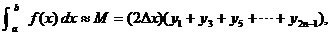 using only the
odd-indexed mesh points. using only the
odd-indexed mesh points.
Since 2n is an even number, we can
apply Simpson’s Rule. Prove that the Simpson’s Rule formula equals the
weighted average 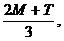 i.e., an average of
midpoint and trapezoid sums with the midpoint sum weighted twice as heavily. i.e., an average of
midpoint and trapezoid sums with the midpoint sum weighted twice as heavily.
|
|
|
M 10/28/13
|
HW due:
1. Using a different color of ink, correct your proof problem from last
Friday. The solution is here.
2. Read §6-3.
3. Write §6-3 #57, 58.
4. Prepare §6-3 #1-54 for oral presentation. (Written notes are permitted but
are not required.) For example, if you are called upon to present #47, you
should instantly say, “By FTC2, 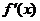 equals cos 3x.” If
called upon to present #35, you should instantly recognize the numerator as
the differential of the denominator, making the antiderivative
ln|1 + sec x| + C. equals cos 3x.” If
called upon to present #35, you should instantly recognize the numerator as
the differential of the denominator, making the antiderivative
ln|1 + sec x| + C.
|
|
|
T 10/29/13
|
HW due: Prepare the review
problems below for oral presentation. Written notes are encouraged but will
not be collected.
pp. 294-295 #1-76 all
pp. 228-229 #4
These will not be graded, but you should (at a minimum) familiarize yourself
with the questions being asked. For example, when we cover #4 on pp. 228-229,
you should already know what a degree-day is, so that we don’t have to spend
time explaining the purpose of the question.
Also note: The functions in #32 and
#33 on p. 295 are called, respectively, the hyperbolic cosine (cosh x,
pronounced so as to rhyme with “gosh”) and the hyperbolic sine (sinh x,
pronounced “sinch”). Try to apply this knowledge
when you get to #64.
|
|
|
W 10/30/13
|
Quizzes (2 of them, 10 pts. each) covering
essentially everything through §6-3.
However, the calculus of formal logic is excluded, since there won’t be enough
time. Other topics discussed in the class but not in the textbook, such as
CRI, are fair game.
|
|
|
Th
10/31/13
|
No additional written HW
due.
|
|