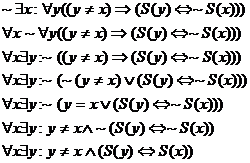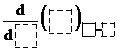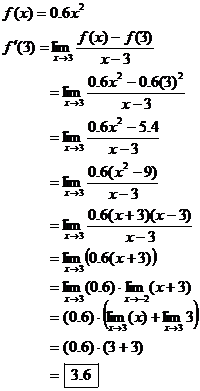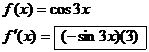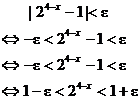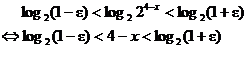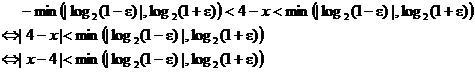|
W 9/4/13
|
First day of class.
|
|
|
Th
9/5/13
|
HW due:
1. Send Mr. Hansen an e-mail. Please use a double underscore (__) at the beginning
of your subject line. Contact information is available at
www.studyofpatterns.com.
2. The calculus is a formal system. Prepare a written list of 5 or 6 other
formal systems that you have experienced in real life. Can any of these
legitimately be called a “calculus”? When writing up your answers, follow the
link for “HW guidelines” at the top of the schedule.
|
|
|
F 9/6/13
|
HW due:
0. Devoe, Cole, Matthew, and Will still need to do #1 in the previous assignment.
If you sent an e-mail, it was lost in cyberspace! Please try again.
1. Read the following Wikipedia articles:
http://en.wikipedia.org/wiki/Predicate_logic
http://en.wikipedia.org/wiki/Logical_not
(stop just before the “Programming” subheading)
2. Note that we will use the symbol ~ to mean “not.” The symbol  is equally valid,
but we will not use it. Simplify each of the following logical expressions,
where A and B refer to atomic statements whose truth value is unknown. is equally valid,
but we will not use it. Simplify each of the following logical expressions,
where A and B refer to atomic statements whose truth value is unknown.
(a) 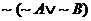
(b) 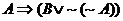
(c) 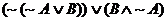
3. Yesterday’s and today’s written assignments will be collected and graded.
Remember that you can use a time log if you are unable to complete the
assignment, provided that you have attempted to do the work and have shown
proper placeholders.
|
|
|
M 9/9/13
|
HW due:
0. All students have now completed assignment #1 that was due on Thursday,
9/5. Thank you for your e-mails!
1. Read the following Wikipedia articles:
http://en.wikipedia.org/wiki/Logical_consequence
(stop before the “Proofs and models” subhead)
http://en.wikipedia.org/wiki/Truth_table
http://en.wikipedia.org/wiki/Logical_equivalence
Note: We will use the symbol “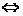 ” for logical equivalence. This symbol is also equivalent
to the word “iff” (if and only if) and indicates
that the expression on the left can be considered to be a definition for the expression on the
right, and vice versa. ” for logical equivalence. This symbol is also equivalent
to the word “iff” (if and only if) and indicates
that the expression on the left can be considered to be a definition for the expression on the
right, and vice versa.
For example, the Isosceles Triangle Theorem (ITT) that you learned in
geometry is a biconditional
theorem that can be written in the form
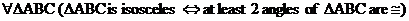
In other words, the presence of 2 congruent angles can be used as an
alternate definition of isosceles. (The standard definition of isosceles is
that at least 2 sides are congruent, but the ITT provides an equivalent
alternate definition.)
2. Given: The universe of quantification is the set of STA freshmen, and S(x)
is the predicate (i.e., propositional function) defined by the rule, “x is a silly person.” Translate each
of the following into good English:
(a) 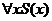
(b) 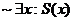
(c) 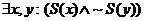
(d) 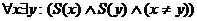
(e) 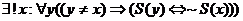
(f) 
(g) 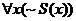
Warning: Part (g) is hard. Try not to fumble it!
|
|
|
T 9/10/13
|
HW due:
Use a truth table in order to prove each of the following. Remember to end
each proof with “Q.E.D.” or the Halmos sign (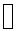 ). ).
1. 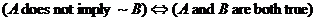
2. 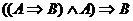
3. 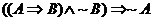
4. 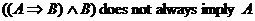
5. 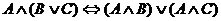
6. 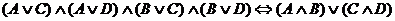
|
|
|
W 9/11/13
|
HW due:
1-7. Negate each of the expressions in #2, parts (a) through (g), from the assignment
due Monday 9/9. In each case, carry the negation sign as far “inside” as you
possibly can, and alter part (e) so that you have a standard existential
quantifier, not a unique existential quantifier. Part (e) is done below as an
example that you can copy into your notes if you wish.
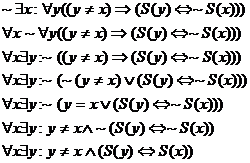
8. The definition of the limit of function f, as its argument x
approaches some constant value c,
is defined as follows:
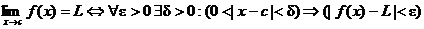
We will discuss what this means in class. For now, simply commit the
definition to memory.
9. Bonus (optional): Prove #3 from the assignment due Tuesday, 9/10. Note: The original version contained a
typo. The conclusion of the theorem should be ~A, but in the original version, the conclusion was A. Sorry!
|
|
|
Th
9/12/13
|
HW due:
1. Explain why the limit definition can be rewritten in this form:
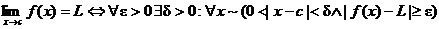
2. Since the limit definition is biconditional, we
can negate both the LHS and the RHS and still have a true statement. Do that,
using the modified version of the RHS found in #1. Note: Standard abbreviations such as “LHS” and “RHS” are found here.
3. Write §2-2 #5-12 all. For #7-12, you may omit part (d) for several of them
to save time, if you wish. Be sure to do part (d) for at least 2 of the
problems, though.
|
|
|
F 9/13/13
|
HW due:
1. Finish the problems from §2-2 if you have not already done so. Do at least
one additional part (d) for #7-12, so that you have a total of at least 3 of
the problems that include part (d).
2. Let y = f (x) = | x |, the absolute value function. Use
your TI-83 or TI-83 calculator to compute the value of 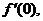 sometimes denoted sometimes denoted 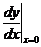 . The keystrokes, assuming you have previously defined Y1
to be abs(X), would be as follows: . The keystrokes, assuming you have previously defined Y1
to be abs(X), would be as follows:
(1). Press the MATH button followed by the 8 key.
(2). (Depending on what model of calculator you have, you will see either nDeriv(
or
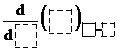
displayed for you as a prompt.
Older calculators have firmware that gives nDeriv(
as the prompt, whereas newer ones have the “dotted box” template that closely
resembles the real math notation. If you have the older style, fill in
nDeriv(Y1,X,0)
and press ENTER. (Remember that the keystrokes to get Y1 to show
up are VARS Y-VARS 1 1. You should have learned
that in previous classes.)
If you have the newer style, simply fill the “dotted boxes” with X, Y1,
and 0, respectively, and press ENTER.
3. The answer your calculator provided in #2 was wrong. Prove this by applying the limit definition for 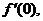 namely namely 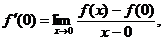 where f (x)
= | x |. where f (x)
= | x |.
Apply the negated definition from yesterday’s assignment in order to prove,
rigorously, that the limit is not
equal to the answer you found in today’s #2.
4. The “left-handed” derivative of the absolute value function at x = 0 is –1. What is the
“right-handed” derivative?
5. Complete the thought: A derivative at a point exists iff
the LH derivative and _________________ both exist as real numbers and
_________________ .
6. Write a formal limit definition of the right-handed derivative of a
function y = f (x) as x approaches c.
|
|
|
M 9/16/13
|
HW due: If you have not already
done so, make sure you have properly executed the negated limit definition in
#3 from Friday’s assignment, and make sure you are completely caught up on
the other old homework problems. Also, get plenty of sleep!
|
|
|
T 9/17/13
|
HW due:
1. Read the green box on p. 48, plus all of §§2-4 and 2-5. Reading notes are
required, as always.
Note: Simply copying the contents
of the box on p. 48 is a waste of time. Why not add value as you make your
notes? For example, you could write “Lim of sums = sum of lims”
for the second boldface heading on p. 48.
Reading notes are permitted to be terse and somewhat illegible. They are for your benefit, not for anyone else’s.
If you wish to keep your reading notes in a spiral notebook instead of on the
same sheet you use for your written HW problems, that is acceptable, as long
as you are able to show each day’s reading notes promptly upon request. Keep
them well-labeled and in order by date.
2. Write §2-3 #13abc (check answer in back before proceeding), 14abc.
3. Prove that if the derivatives of functions f1, f2,
f3, . . . all exist at a
point x = c, then the derivative (at x
= c) of the sum of those functions
equals 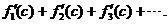 In other words,
“Deriv. of sum = sum of derivs.” In other words,
“Deriv. of sum = sum of derivs.”
4. Prepare §2-4 #1-20 for oral presentation only. (You may make notes in the
margins of your textbook if you wish, but that is not required.)
5. Write §2-4 #60, 68, 70ab.
|
|
|
W 9/18/13
|
HW due:
1. Read §2-6. Reading notes are required, as always.
2. Write §2-6 #13.
3. Let Q(x) denote the difference quotient function, 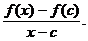
For problems 1-19 odd in §2-4, let c
denote the marked point in cases where c
is not already the marked point, and answer the following questions for each
illustrated graph. Also assume that the horizontal and vertical scales are
equal. (Warning: On the AP exam,
you should not assume equal
horizontal and vertical scales.) As you can see, #1 is done for you as an
example. Because this involves a lot of repetition, it is recommended that
you make a table and fill in the remaining rows for #3, 5, 7, etc. It is
permitted to 3-hole punch a printout of this portion of the web page and put
it in your binder.
(a) Tell whether or not Q(x) has a left-handed limit at x = c. Use correct notation.
(b) Tell whether or not Q(x) has a right-handed limit at x = c. Use correct notation.
(c) Tell whether or not Q(x) has a 2-sided limit at x = c. Use correct notation.
(d) Tell whether or not 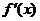 has a left-handed
limit at x = c. Use correct notation. has a left-handed
limit at x = c. Use correct notation.
(e) Tell whether or not 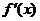 has a right-handed
limit at x = c. Use correct notation. has a right-handed
limit at x = c. Use correct notation.
(f) Tell whether or not 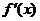 has a 2-sided limit
at x = c. Use correct notation. has a 2-sided limit
at x = c. Use correct notation.
(g) Tell whether or not 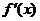 exists when x = c. Use correct notation. exists when x = c. Use correct notation.
(h) Tell whether or not 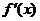 is continuous at x = c. IMPORTANT: Give a
reason for your answer. is continuous at x = c. IMPORTANT: Give a
reason for your answer.
|
|
|
|
(a)
|
(b)
|
(c)
|
(d)
|
(e)
|
(f)
|
(g)
|
(h)
|
|
|
|
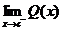
|
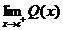
|
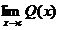
|
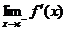
|
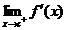
|
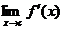
|
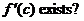
|
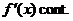 at x=c? at x=c?
|
|
|
1.
|
yes, about 0.4
|
no, 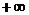 or DNE or DNE
|
DNE
|
yes, about 0.4
|
yes, about 0.4
|
yes, about 0.4
|
no*
|
no, since 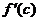 DNE DNE
|
|
|
3.
|
|
|
|
|
|
|
|
|
|
|
5.
|
|
|
|
|
|
|
|
|
|
|
7.
|
|
|
|
|
|
|
|
|
|
|
9.
|
|
|
|
|
|
|
|
|
|
|
11.
|
|
|
|
|
|
|
|
|
|
|
13.
|
|
|
|
|
|
|
|
|
|
|
15.
|
|
|
|
|
|
|
|
|
|
|
17.
|
|
|
|
|
|
|
|
|
|
|
19.
|
|
|
|
|
|
|
|
|
|
|
|
* Even though 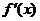 has matching left-
and right-handed limits at x = c = 2, that is not the criterion for
the existence of has matching left-
and right-handed limits at x = c = 2, that is not the criterion for
the existence of 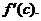 By definition, By definition, 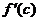 exists iff the left- and right-handed limits of the difference quotient function exist and
are equal. exists iff the left- and right-handed limits of the difference quotient function exist and
are equal.
|
|
|
Th
9/19/13
|
HW due:
1. Read §3-2, the green box at the top of p. 84, §3-3, and the green box on
p. 89.
2. Write §2-6 #7.
3. Write p. 73 #R6bc.
4. Write §3-2 #3, 4, 5-11 odd. Warning:
The answers in the back of the book for #3a, 5, 7, 9, and 11 are completely
inadequate. See below for an example of what you should provide in terms of
work.
Example (#3a)
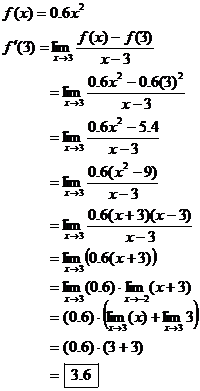
|
|
|
F 9/20/13
|
NOTICE: According to Dr. Labaree, Upper School Head,
B period will run as usual. The assembly honoring Jonathan Ogden ’92 is
scheduled to conclude well before 9:40 a.m.
HW due:
1. Read §§3-4 and 3-5.
2. Write §3-4 #32, §3-5 #8abcde.
3. Write a “math symbol” version of the EVT. Use a style similar to what we
did in class with the IVT.
4. Ask a friend to sketch on your
homework paper a function whose graph has some interesting cusps,
curves, discontinuities, and maybe an asymptote or two. (If you can’t find
any friends, copy the curve sketched on p. 359 onto your homework paper.)
Then, on a different set of axes but with the x-axis points lined up beneath their corresponding points on the
function sketch, sketch the derivative function.
|
|
|
M 9/23/13
|
HW due:
1. Read §§3-6 and 3-7.
2. Write §3-6 #7, §3-7 #3-22 all, 24. Note that the statement of the problem
is required in each case. Do not simplify your answers for #3-22. See the
example shown below.
Example:
3.
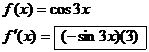
|
|
|
T 9/24/13
|
HW due: Review problems as
listed below.
1. Translate each of the following into mathematical notation, using “Let”
statements to make your notation clear. Then negate the statement
symbolically and translate the negated version back into English. The first
one is done for you as an example.
(a) No pain, no gain.
Solution:
Let P = existence of pain
Let G = occurrence of gain
Original: 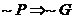
Negation: 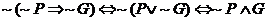
In English: Gain occurs together with a lack of pain.
(b) For any fool, there is a greater fool somewhere.
(c) When the going gets tough, the tough get going.
(d) If it’s not special, you didn’t find it at our store.
(e) For every difficult problem, there is a simple, straightforward solution,
and it is wrong.
(f) There’s no business like show business.
(g) That’ll happen when pigs fly.
(h) There’s someone for everyone.
(i) You can fool some of the people all of the
time, but you can’t fool all of the people any of the time.
2. Use a truth table to prove that the implication operation (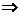 ) is transitive. ) is transitive.
3. Write an equation for the derivative if 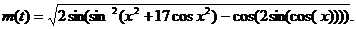
4. Let f (x) = 1 + 24 – x.
(a) Compute 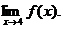 Give a sentence of
justification for the method you used. Give a sentence of
justification for the method you used.
(b) Use the definition of limit and an epsilon-delta proof to show that the
limit is what you claimed in part (a).
5. Use the definition of derivative to compute 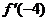 if f (x)
= x2 + 6x – 2. Here, you are allowed to assume
all the standard limit properties instead of having to pretend (as in #4b)
that you didn’t know them. if f (x)
= x2 + 6x – 2. Here, you are allowed to assume
all the standard limit properties instead of having to pretend (as in #4b)
that you didn’t know them.
6.(a)State the formal definition of what it means for 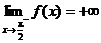 . .
(b) For f (x) = sec x, find a
number 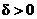 such that f (x)
> 1000 whenever x is within such that f (x)
> 1000 whenever x is within 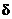 units of units of 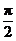 on the negative side
(i.e., approaching on the negative side
(i.e., approaching 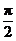 from the left). from the left).
7. Let h(t) = 3 + 5t–1.6
be the height function of a particle moving as a function of time t (in seconds). Height is in cm.
(a) Write an equation for the velocity function, including units of measure.
(b) Write an equation for the acceleration function, including units of
measure.
8. Let f (x) = (sgn x)(0.5x2).
(a) Show that f is C1 but not C2.
(b) Can the EVT be used to prove that 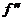 has a minimum on
[–3, 3]? Why or why not? has a minimum on
[–3, 3]? Why or why not?
(c) Can the EVT be used to prove that 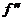 has a maximum on
[–3, –1]? Why or why not? has a maximum on
[–3, –1]? Why or why not?
9. Given: All power functions are continuous.
Prove: There is a positive number x whose square is 2.57. (In other words, the principal square
root of 2.57 exists.)
Hint: Consider the power function y = x2.
|
|
|
W 9/25/13
|
Here is a sample
test from a previous year to illustrate one possible format and level of
difficulty. This year’s test covers
a different mix of material and may not resemble the sample test.
Test (100 pts.) on all material covered so far, including the calculus of
formal logic and all classroom discussions. Textbook knowledge is expected
through §3-7, plus the meaning and basic usage of the antiderivative
symbol (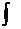 ). ).
As promised, here is the proof of #4b from yesterday’s review problems:
Claim: 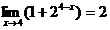
Proof: We want to show that 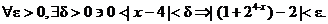
Equivalently, we say 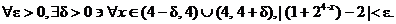
Let 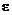 be specified, and wlog, assume be specified, and wlog, assume 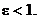 Justification: All
we have to do is produce Justification: All
we have to do is produce
a value of 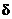 that makes the final
inequality true for all x in a
punctured that makes the final
inequality true for all x in a
punctured 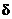 -neighborhood of -neighborhood of
4, and any 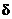 that does that when that does that when 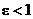 would work equally
well for would work equally
well for 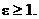
The final inequality is
true iff
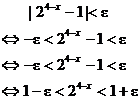
Since 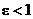 (see justification
above), we can take base-2 logarithms. The base-2 logarithm (see justification
above), we can take base-2 logarithms. The base-2 logarithm
function is monotone
increasing on its domain and hence order-preserving. [Translation: We
don’t need to flip the
direction of the inequalities the way we do when, for example, taking
reciprocals or
multiplying through by a negative number. Remember learning that in earlier
courses?]
The final inequality,
our “goal,” becomes
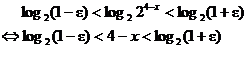
In other words, the
“goal” inequality is true iff 4 – x is between 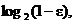 which is a which is a
negative number, and 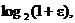 which is a positive
number. Which of those numbers has which is a positive
number. Which of those numbers has
the smaller absolute
value? As long as we restrict 4 – x
to those even tighter bounds, we can
certainly follow the
bidirectional implication arrows backwards to satisfy our “goal”
inequality. Note that
trapping 4 – x between a negative
number and a positive number
can be made more restrictive (and hence still able
to satisfy the “goal” inequality) if we require
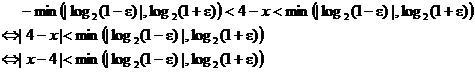
Remember that we
assumed wlog that 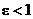 . The RHS, namely . The RHS, namely 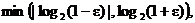
becomes our logical
choice for 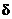 . Since we can always
produce such a . Since we can always
produce such a 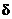 , regardless of the value , regardless of the value
of 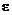 , we can always satisfy the , we can always satisfy the 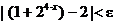 inequality when
choosing x from a punctured inequality when
choosing x from a punctured
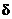 -neighborhood of 4, as required by the limit definition. -neighborhood of 4, as required by the limit definition. 
[Note: The “goal” inequality in
problem #4b happens to be equally true if the 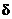 -neighborhood from which x is chosen is not punctured, but the limit definition does not require that. The reason is that
we want to be able to define a limit regardless of the value that f might have at the point in question.
For example, imagine that f (4) in
this problem were redefined to be some crazy value like 288.7, or imagine
that f (4) were DNE. Even so, we
would want to be able to prove -neighborhood from which x is chosen is not punctured, but the limit definition does not require that. The reason is that
we want to be able to define a limit regardless of the value that f might have at the point in question.
For example, imagine that f (4) in
this problem were redefined to be some crazy value like 288.7, or imagine
that f (4) were DNE. Even so, we
would want to be able to prove 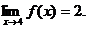 We make that
possible by keeping only a punctured
neighborhood as part of the limit definition.] We make that
possible by keeping only a punctured
neighborhood as part of the limit definition.]
|
|
|
Th
9/26/13
|
HW due: Read §§3-8 and 3-9.
Reading notes are required, as always.
|
|
|
F 9/27/13
|
HW due: Write §3-8 #1, 2,
§3-9 #13, 14, and 3-24 mo3. For #13, see if you can obtain the answer in the back
of the book before you peek. Then, apply the technique of #13 to #14. Form VI
students may submit this assignment on Monday without penalty.
Hint: This is a good technique in
general. When unable to complete an even-numbered problem that has been assigned,
choose an odd-numbered problem that is similar to it, and see if you can
“reverse engineer” the method used.
|
|
|
M 9/30/13
|
No additional HW due.
|
|