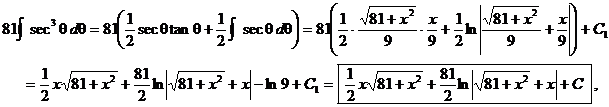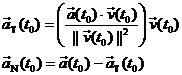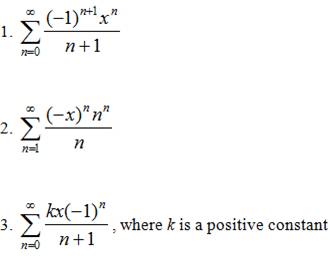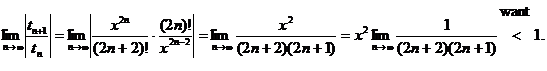Welcome to the HappyCal Zone

(Honors AP Calculus BC, Period B)

Are you nervous when you see NCWEE? concerned when you see CIRC? perturbed when you see PBC? Visit Mr. Hansen’s fabled abbreviations page to make sense of those cryptic markings you see on your papers.

Schedule at a Glance (see archives for older entries) Written assignments should follow the HW guidelines.
Th 1/23/14	Classes resume. In class: Free-response group quiz.
F 1/24/14	No additional HW due. (Form V had a required event at school on Thursday night.) In class: Multiple-choice group quiz.
M 1/27/14	Mozart’s birthday: No additional HW due.
T 1/28/14	No additional HW. (No special occasion.) Bonus opportunity (optional): Up to 2 bonus points will be awarded for a clean, neat proof that the area between the graphs of the limaçon r = 2 – cos and the circle r = cos equals not In other words, you need to explain clearly how a “good” student could reach the wrong answer of and where the conceptual problem probably arose.
W 1/29/14	HW due: Read §9-4; write §9-3 #3-48 mo3.
Th 1/30/14	HW due: Read §9-5 and memorize (if you have not already done so) the identities at the bottom of p. 452.
F 1/31/14	HW due: Read §9-6. In class: Finish learning how to perform trigonometric substitution. Begin by carrying §9-6 #4 to completion. and the original integral becomes which agrees with the result we obtained by using the table of integrals. The answer also agrees with WolframAlpha.com, though WolframAlpha.com expresses the second term using an inverse hyperbolic sine function.
M 2/3/14	HW due (although it will not be collected until Tuesday): 1. If you have not already done so, work §9-6 #4 to completion, using the 1/31 calendar entry for reference. 2. Write §9-6 #8, 12, 14, 16, 18. Note: Both #16 and #18 should be done two ways. 3. Read the paragraph of text above #19 and #20, as well as the paragraph of text above #21 and #22. Optional: Write #20, 22. These skills, which once formed a significant part of a standard calculus course, are now delegated to WolframAlpha.com.
T 2/4/14	HW due: Read §9-7 and this tutorial on partial fractions; write problems 1-5 all and 7-15 odd from the online tutorial. (Note that solutions are provided. However, you should try to solve the problems on your own before checking the solutions.)
W 2/5/14	HW due (everyone): Prove that the solution (y) of the diffeq. experiences its maximum rate of growth at the time when y equals half the carrying capacity of 700. HW due (required for those who skipped AMC 12 yesterday afternoon, optional for those who sat for the competition): Write #6, 8, and 10 from the tutorial on partial fractions.
Th 2/6/14	HW due: Read §9-9; write §9-8 #1-6 all, plus your choice of #8 or #10. Hint for #5 and #6: Consider cases (x > 0, x < 0) and combine at the end.
F 2/7/14	HW due: Read §9-10 and the preamble to #23 and #24 on p. 479; write §9-9 #6, 14, 18, 25, and explain (briefly) why #23 and #24 were not assigned except for the reading of the preamble.
M 2/10/14	HW due: Prepare §9-11 #1-100 for oral presentation. If the problem is easily done by inspection with no work (e.g., #51), be prepared to give the answer. If the problem is harder (e.g., #29), be prepared to state what technique(s) could be used to solve the problem. For example, #29 can be done in a multitude of ways, and you should be prepared to state all of them: 1) by trig. sub. after completing the square, 2) by partial fractions involving A/(x + 5) and B/(x – 1), 3) by looking up the standard form in a table of integrals after completing the square, or 4) by using WolframAlpha.com. Note: You do not get credit for saying “WolframAlpha.com” if the answer is so easy that you should be able to do it in less time than it would take to key the problem in and press the Enter key. The purpose of this exercise is to build your skill in quickly identifying what approach is appropriate.
T 2/11/14	HW due: Read §9-10 and §10-2; write §9-10 #1-19 all (keeping the word “lim” in your work until almost the end each time), and read #24.
W 2/12/14	HW due: Read §10-3; write §10-2 #5, 6, 7, 8, 10, 12, §10-3 #1, 3, 11, 13.
Th 2/13/14	HW due: Review problems as listed below. You will probably not finish all of these by today (Thursday). Keep a time log in case you do not finish. However, if school is canceled, all of these will be collected Tuesday, 2/18, before you take your test. 1. Do the chapter test on pp. 501-502. Omit #10 and #11a. For #13b, derive the reduction formula before using it. Note: There is a blatant typo in the reduction formula, but it is so obvious that you should be able to figure it out. 2. Write #13 on p. 511. 3. Write #15 on p. 516.
F 2/14/14	No school (teacher professional day).
M 2/17/14	No school (holiday).
T 2/18/14	Test (100 pts.) over all of Chapter 9, §10-2, and §10-3. This is the coverage that was previously announced in class. As usual, there is a 4-point bonus for perfect attendance. For the more advanced types of trigonometric substitutions and partial fraction decompositions, you are required to identify the required method but not actually work the problems. Partial fraction decompositions that you are required to complete on the test will be limited, as on the AP exam, to non-repeated linear factors only.
W 2/19/14	No additional written HW due.
Th 2/20/14	HW due: 1. Read §10-4. 2. Work through the related rates tutorial. As you work through the 3 illustrative examples (balloon problem, ladder problem, and watch problem), make a sketch for each one. Go through the steps, showing the work on your own HW paper, and make sure that you obtain the same answers as those that are given. 3. Work through these 2 practice problems. The work does not need to be presentation-quality. However, do compare your answers against the solution key to make sure that you understand what you are doing and have corrected your answers. 4. Write §10-4 #13, 14.
F 2/21/14	HW due: Read §10-7; write §10-5 #1, 2, 6, 7, §10-6 #6, 11.
M 2/24/14	HW due: Read §10-7 again; write §10-6 #12, §10-7 #1 (make a sketch in your HW paper if you don’t have access to a photocopier), and the proof below. Remember to use double bars (not single bars) for vector norms, and put an arrow over any letter used to represent a vector (since you can’t conveniently write in boldface). Proof Problem Prove that the tangential and normal components of acceleration at time t = t0 are given by the formulas
T 2/25/14	HW due: 1. Wlog, explain how to rewrite any 2- or 3-dimensional vector in terms of unit vectors 2. Using #1 as a lemma, and using the definition of dot product as the product of norms and the cosine of the included angle, prove that the dot product of any pair of 2- or 3-dimensional vectors equals the sum of the products of the corresponding coordinates.
W 2/26/14	HW due: 1. Read §11-2, especially Example 2 on pp. 559-560. 2. Write §10-7 #4, 11. 3. Write §11-2 #1, 5. 4. (Optional.) Without using the Law of Cosines or the alternate definition of <a, b> · <c, d> = ac + bd, prove that the dot product distributes over addition. In other words, show that for any vectors where dot product is defined by the product of the norms and the cosine of the included angle, we have
Th 2/27/14	HW due: 1. Read §11-3. This is yet another application of variable-factor products. 2. Write §11-2 #6, §11-3 #6, 12. For #12, use the fact that a spherical shell has volume equal to the product of its surface area, namely and dr.
F 2/28/14	HW due: 1. Read the green boxes on p. 570 and p. 577. These are not part of the AP curriculum, but they are certainly worth knowing about. 2. Read §11-6. 3. Write §11-6 #4, 8, 12.
M 3/3/14	Snow day.
T 3/4/14	HW due: Read §12-1, §12-2, and #8d on p. 606; write §12-1 #1-7 all, §12-2 #8abc.
W 3/5/14	NORMAL CLASS PERIOD. The study hall originally scheduled for today has been canceled. HW due: For each of these power series, (a) write out the first 5 or 6 terms followed by an ellipsis (. . . ), (b) categorize the power series as conditionally convergent, absolutely convergent, or divergent on the interval (–1, 1), and (c) provide an explanation for your answer to part (b). Note: Since all power series in x are convergent when x = 0, ignore what happens at x = 0 when determining your answer to part (b). You may use a calculator when exploring the behavior of the series for various values of x.
Th 3/6/14	HW due: Read §12-3; write §12-2 #2, §12-3 #1-11 all.
F 3/7/14	HW due: 1. Read §§12-4 and 12-5. 2. Change the “1” in the green box at the top of p. 616 to an “a” (typo correction). 3. Memorize the “Eight Well-Known Power Series” on p. 616 as well as their associated intervals of convergence. 4. Write §12-4 #1.
M 3/10/14	HW due: Get some good sleep! Enjoy the beautiful weekend weather!
T 3/11/14	HW due: Write §12-5 #1-8 all, 9-24 mo3, 26, 29, 30.
W 3/12/14	HW due: Read §12-6; write §12-6 #1-13 all, 21-24 all.
Th 3/13/14	HW due: Finish the assignment due yesterday, and read this reference about the LCT.
F 3/14/14	Pi Day! HW due: Read §12-7, including the green box on p. 640. Make sure that you are thoroughly familiar with the meaning and contents of the lower green box on p. 635. Then write §12-7 #5-14 all.
M 3/17/14	Snow day (no school). Happy St. Patrick’s Day!
T 3/18/14	HW due: Read §12-8. This is difficult material, and it is recommended that you read it at least twice. Reading notes are required, as always. This is your final reading assignment for the year. In class: Review for tomorrow’s quiz.
W 3/19/14	Big Quiz on all recent material. Sample questions are below. 1. Find a Maclaurin series for f (x) = Prove that your series has an infinite radius of convergence, even though f itself is undefined at x = 0. 2. The Taylor series is known to converge when x = 4.7. Find the smallest possible value for the radius of convergence. Solutions: 1. cosh x – 1 = Divide through by x^2 to get Apply the ratio test: The inequality holds for all real x, since = 0. 2. The center of the expansion is 3. Since x = 4.7 is within the interval (technically, disk) of convergence, the radius is at least 1.7.
	Spring break. Your quarter grade will be e-mailed to you by approximately March 31 or April 1.
M 3/31/14	HW due: Crack the binding on your AP review book, and start reviewing. Set a goal of 10 minutes per day during the break. Daily exposure is more important than massive exposure.
T 4/1/14	HW due: Bring in a written log of your AP review (35 minutes or more). Check your answers, and mark corrections in a different color of ink. Allow 2 minutes for each multiple-choice problem without calculator, 3 minutes for each multiple-choice problem with calculator, and 15 minutes for each multi-part free-response problem. Free-response problems can be found at the College Board website. In 35 minutes, you should be able to complete a dozen or more problems. In class: Begin review of Chapter 12 and general AP review. A detailed log sheet will be distributed today or tomorrow so that you have a designated place for recording your AP review.
W 4/2/14	HW due: 1. Continue your nightly AP review. A minimum of 35 minutes is expected. Use a time log. 2. (Optional.) Use (a) the AST error bound and (b) the Lagrange error bound to determine how many terms of the Maclaurin series for cosine are needed in order to compute cos x within an absolute tolerance of 0.0002, when x is between –4 and 4 radians. 3. (Optional.) Explain briefly why nearly all high-level computer languages define their built-in sine, cosine, and tangent functions in terms of radian arguments, not degree arguments. Note: If you do problems 2 and/or 3, you may count them toward your 35-minute time log requirement.
Th 4/3/14	HW due: Download the AP review log and start logging your nightly AP review by subject/topic area. Note: If you are unable to print this out at home, make a written log on 3-ring binder filler paper as always, and then transfer the log data in class today. Spare copies will be provided for anyone who still needs one.
F 4/4/14	HW due: In addition to your AP review, make sure to do #2a from the W 4/2/14 calendar entry. This was announced during class.
M 4/7/14	HW due: AP review.
T 4/8/14	HW due: AP review. In class: Quiz (possibly 2 quizzes).
W 4/9/14	HW due: AP review.
Th 4/10/14	HW due: AP review. Another quiz is extremely likely.
F 4/11/14	HW due: AP review.
M 4/14/14	HW due: AP review, plus at least one “vexing question” (see below). In class: Review for test. Bring at least one “vexing question” from the book. If you have no questions that have vexed you personally, then bring a question that you think would make a good test question for tomorrow’s test. This will be scored.
T 4/15/14	Test (100 pts.) on Vectors (§10-7), Chapter 11, and Chapter 12. HW due: Mixture of AP review and studying for the test. Keep a written time log. You may split your time in any proportion than you wish (e.g., 50/50 between general AP review and focused studying for today’s test, or 100% for general AP review, or 100% for the test). The test will be pitched for a 40-minute time limit. There may be some AP-style problems, but if there are, they will be timed and scored using AP rules (15 minutes per multi-part FR problem, 2 minutes per MC without calculator, 3 minutes per MC with calculator).
W 4/16/14	HW due: AP log, as always. Form VI students have Alumni Day activities today and must get scanned tomorrow, before class.
Th 4/17/14	HW due: AP log. Form VI students should arrive on time to get scanned for yesterday as well. All others may arrive at 9:00 a.m.
F 4/18/14	HW due: AP log, as always. In class: Graded quiz.
M 4/21/14	HW due: AP log, as always. In class: Ungraded quiz (CFU).
T 4/22/14	HW due: AP log, as always. In class: AP multiple-choice quiz.
W 4/23/14	HW due: AP log, as always. In class: Another AP quiz.
Th 4/24/14	HW due: AP log, as always. In class: Another AP quiz is likely.
F 4/25/14	TBD.
M 4/28/14	Practice AP Exam (70 points). Today’s format is multiple-choice, no calculator. You will have 22 problems in 43 minutes (slightly shorter than the real AP exam, which is 28 problems in 55 minutes). Class will begin at 9:02 (7 minutes late) and will end at exactly 9:45. We use Naval Observatory time, not the STA clocks. Most of the STA clocks are nearly 3 minutes slow. If you are not able to be in your seat, ready to begin, at 9:02, then the door will be opened exactly once, at approximately 9:07. However, no additional time will be provided. If you have an excused absence on any of the practice AP exam days, you must contact Mr. Hansen. Makeups after the fact will not be offered. If you miss one of the practice exams, it will simply be dropped, and the 2 other scores will be counted. If you take all 3 exams (highly recommended!), the lowest of the 3 scores will be dropped.
T 4/29/14	Practice AP Exam (70 points). Today’s format is multiple-choice, with calculator. You will have 17 problems in 50 minutes. Class will begin on time at 8:55 and will end at exactly 9:45. If you are not able to be in your seat, ready to begin, at 8:55, then the door will be opened exactly once, at approximately 9:00. However, no additional time will be provided.
W 4/30/14	Practice AP Exam (70 points). Today’s format is a 50% scale model of the real Part II. We will begin at 9:00 and will end at exactly 9:45. If you are not able to be in your seat, ready to begin, at 9:00, then the door will be opened exactly once, at approximately 9:05. However, no additional time will be provided. On the real AP exam, you have 30 minutes to complete 2 free-response problems with calculator, then 60 more minutes to work on 4 additional problems without calculator (as well as any no-calculator portions from #1 and #2 that you wish to continue working on). Today’s format will be exactly half: Half as many “with calculator” problems (1 instead of 2), half as many “without calculator” problems (2 instead of 4), and half as many minutes to work on everything (45 instead of 90).
Th 5/1/14	HW due: AP review, as always. In class: Go over answers from the past 3 days, resolving all discrepancies and points of confusion.
F 5/2/14 through W 5/7/14	HW due: AP review, as always. Check out this huge collection of AP multiple-choice problems! Thanks to Devoe for the link. A partial answer key is also available.
W 5/7/14	HW due: Sleep! If you spend time reviewing the cram sheet, be sure to document that on your log sheet. However, sleep is even more important. Time spent on the cram sheet is fully creditable toward your HW log. AP Exam (Trapier Theater, 8:00 a.m.–11:45 a.m.) What to bring: Several sharpened pencils, graphing calculator, spare batteries. Leave in car or locker: Cell phone, book bag, scratch paper. Snacks will be provided at the break, approximately 10:10 a.m. The snacks are courtesy of Ms. Dunn. Be sure to thank her!!
Th 5/8/14	No additional HW due. However, your log sheets will be checked one last time. In class: Excel.
F 5/9/14	HW due: Practice Excel. Be prepared to hit the ground running when we start today. Familiarity with SHIFT + arrow keys, CTRL + arrow keys, and SHIFT + CTRL + arrow keys is assumed and will not be retaught. Practice on your own, or ask a classmate for help.
M 5/12/14	HW due: Practice your Excelcise (see 10/28/2010 calendar entry here). Eventually, you have to be able to perform all the listed steps within 5 minutes. The record time, set by Jared Heath in 2013, is about 2 minutes.
T 5/13/14	HW due: Continue practicing. In class: Timed Excelcise runs. If you don’t pass, you will have to come in on your own time to make a successful run. Everyone must pass.
W 5/14/14	No additional HW due, except to keep practicing if you have not yet passed the Excelcise ordeal. In class: Modeling.
Th 5/15/14	In class: Simulation.
F 5/16/14	Quiz on recent class discussions.
M 5/19/14	Another quiz. Please note, five (5) students still need to pass the Excelcise. You may come in during F period or after school.
T 5/20/14	Another quiz is possible. Please note, Devoe, Matthew, Nick, Andrew, and Yi still need to pass the Excelcise. You may come in during F period or after school.
W 5/21/14	Field Trip to the NSA/National Cryptologic Museum. Coat and tie are not required (per yesterday’s lunch announcement by Headmaster Wilson), but please wear a shirt with a collar. We are ambassadors of STA and want to represent the school well. Bus departs at 8:00 a.m. from the service road near the Martin Gym. We will be back on campus by 1:15 p.m., in time for lunch. Note: If you are unable to go on the field trip, you must do this alternate assignment (do problems 1-8 all, and ignore the indications about “Form”). Turn in your alternate assignment at lunch to Mr. Hansen at table 38. The alternate assignment will be graded.
Th 5/22/14	Probability simulations.
F 5/23/14	Statistical simulations (simulation of sampling distribution of a statistic). Last day of class.
F 5/30/14	Final Exam, 8:00–10:00 a.m., SB-201/202. You will be given a blank blue book and 120 minutes to fill it. Your question is, “Using your own words, tell the story of the calculus as you have organized it in your own mind. Tie together the important themes of the course, showing how you made sense of them. Diagrams and illustrative examples are welcome.” Complete sentences are required. Grammar counts. Spelling counts, but only a little bit. You can indemnify yourself from spelling penalties by using standard abbreviations or writing “(sp.?)” after words whose spelling you are unsure about. For example, if you can’t remember how to spell “infinite,” you could write “inf. series” instead of “infinite series” and still receive full credit. No notes are permitted. An essay of an hour’s length is generally sufficient to earn full credit, but you will be given the full 2-hour period if you desire. Underclassmen: This exam is a required component of your course grade. It will be weighted as 20% of your second semester average. Seniors: You may wish to take the exam as a way of boosting your grade. In previous years, almost all seniors who have sat for this exam have managed to increase their average. If for some reason the exam does not help your grade, it will be dropped.

Essential Links:
-- STA School Handbook
-- College Board: AP Calculus BC Course Description
-- Eric Weisstein’s World of Mathematics, the Web’s most extensive mathematics resource (no kidding!)
-- WolframAlpha.com, a site that I possibly shouldn’t tell you about . . .

Extra Help:
-- Karl’s Calculus Tutor for first-year students
-- Calc101.com, another site I might not want to tell you about (click it and you’ll see why)
-- Temple University: Calculus on the Web (COW)

Links Based on Class Discussions:
-- Troy’s Integral Approximation Thingy: a neat JavaScript application for Midpoint Rule, Trapezoid Rule, Simpson’s Rule, etc.
-- The “RiemannSums Applet” found by John S. (actually shows you the rectangles or trapezoids)
-- Chris and Andrew’s proof that Simpson’s Rule is a weighted average of the Midpoint and Trapezoid Rules
-- Braxton’s direct proof of FTC2
-- Proof that FTC1 implies FTC2 and conversely
-- Related rates tutorial and practice problems
-- Partial fraction decomposition tutorial with sample problems and solutions, courtesy of the University of California at Davis

Links for AP Preparation:
-- Real sample AP questions from the College Board
-- A huge collection of AP multiple-choice questions
-- AB Calculus Cram Sheet
-- BC Calculus Cram Sheet (courtesy of Will Felder and Mr. Hansen)
-- “Stuff you MUST know cold” (link to another AP calculus teacher’s site; requires Adobe Acrobat reader)
-- Review question logsheet (requires Microsoft Excel); also available are old versions for 2003, 2009, 2010, 2011, and 2012.
-- Permitted features for graphing calculators on the AP examination
-- Actual college tests from Mr. Hansen’s alma mater (great practice!) Note: MATH 121 is the calculus course I took back in the (ulp!) 1970s.
-- Multiple choice practice #1 with answer key
-- Multiple choice practice #2 with answer key
-- First semester recap (recycled from my 2006-07 IntroCal class, for which this handout served as a full-year recap)

Fun Links:
-- Homemade “Segway”-like balancing scooter uses a fair amount of calculus!
-- Mathematicians as depicted in the movies (Good Will Hunting, etc.)
-- An Algebra II problem that has a calculus flavor to it. (This is problem #26 from §11-7 of Foerster’s Algebra and Trigonometry: Functions and Applications.) The problem is to determine which sweepstakes prize is better: a $20,000 lump sum or $100 a month for life. Assume 4% annual interest compounded monthly. In part (d), the challenge is to determine how the answer changes if the interest rate changes to 7%.
-- The Mt. Sinai problem and two variations
-- The astonishing Bailey-Borwein-Plouffe algorithm for calculating pi to any desired decimal place
-- Sound wave analysis (harmonics, Doppler shift, etc.), excellent site developed by students at TJHSST in Virginia
-- Good problems (some calculus, some not)
-- More fun links on Mr. Hansen’s home page

Serious Links:
-- Summer math camps for talented high school students
-- Click here for other serious links

---

Return to Mr. Hansen’s home page

Return to Mathematics Department home page

Return to St. Albans home page

Last updated: 24 May 2014