Instructions: This question will be scored holistically on a scale of 0 to 4. Justify your work. Show steps clearly and, to the best of your ability, in a logical sequence. Complete sentences are not required, but clarity of presentation is essential. Unlike on the real AP exam, half points may be allowed. This question, together with the two questions you did in class, will be worth 80 points.
You cannot use any help except for your formula sheet and calculatoróno friends, no tutors, no Internet, no phone calls, no "Stat Tests" handout, no additional TI-83 programs after the test has started, and no books or notes other than pp.475-482 of your Barronís book (marginal scribbles OK). If you have a question, leave e-mail message or call 703-599-6624.
Write on your own paper, please. Use a single "X" (no erasing needed) to mark portions that you wish to be ignored during grading. Calculator notation is strongly discouraged.
Important: Either here or at the end of your last page, sign an honor pledge. ("On my honor as a St. Albans student, I certify that I have used only my formula sheet and calculator to answer this problem. Signed, _________________________________ .") Then, fill in the following information:
Start time: _______________
End time: _______________
Elapsed time: _______________
3.
A quincunx is a device that attempts to illustrate the random motion of a ball as it falls through a lattice of pegs or nails. (See illustration.)
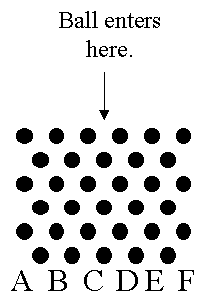
Note: Large round dots indicate pegs or nails seen on end. The pegs are held in place by two sheets of glass that lie in planes parallel to the paperís surface.
By tradition, a quincunx is usually constructed so that the chances of branching left or right are 50/50 at each level. In other words, the probability of reaching position A (5 left branches in a row) would be 1/25, or 1/32. The probability of reaching position B would be 5/32 (LLLLR, or LLLRL, or LLRLL, or LRLLL, or RLLLL, where the probability for each is 1/32 and hence 5/32 altogether). The probabilities for positions C through F can be calculated similarly.
However, suppose that we have constructed a "SUPER QUINCUNX 2000" in which the probability of branching left is always 0.6, independent of what has happened before, and the probability of branching right is always 0.4. We will drop 2000 balls through the Super Quincunx (hence its name) and will record how many go into each of the 6 possible bins, A through F. Note that it takes exactly 5 branches, in some combination of lefts and rights, for a single ball to reach one of the bins at the bottom of the quincunx.
(a)
Explain concisely why the Super Quincunx 2000 produces a binomial distribution for the numbers of balls in bins A through F. If you choose to relabel the bins, be sure to do that clearly.
(b)
Clearly identify and state the two numeric values of the parameters of the binomial distribution for the Super Quincunx 2000. No work needed.
(c)
Compute, showing some work, both the probability that a ball lands in bin D and the expected number of balls in bin D for the Super Quincunx 2000.
(d)
The Las Vegas Quincunx Commission, following a test of 2000 balls, has filed a complaint alleging that the Super Quincunx 2000 does not follow the claimed distribution for a 60/40 split favoring the left branch. According to the Commissionís data, the proportions are as follows:
Bin
A
B
C
D
E
F
Total
Sample Proportion
7.1%
24.3%
34.15%
24.45%
8.75%
1.25%
100%
Which bin(s) probably made the Commission most suspicious? Is the Commissionís complaint justified? You may abbreviate your work, and you need not show all the computations where several are very similar. However, if you re-use any results (for example, from part (c) above), be sure to justify them briefly again here, since different parts of AP problems may be graded by different people. Show steps clearly enough to indicate that you know exactly what you are doing. Write your conclusion in the context of this problem.