Instructions: Show all work and use correct notation. Checking with friends is permitted, but copying will be treated as an honor offense. If you are computing an angle, be sure to show the appropriate inverse trigonometric function (arcsin, arccos, or arctan). For full credit, give answer in the units requested and to the precision requested. The answers are 1702 sq. ft. for #1 and 15°07' for #2.
1.
Mortimer has a yardstick marked in inches, a long rope, and a protractor. His task is to compute the area of a rectangular gymnasium floor. Clearly, there is an easy (if boring) way to do this using the yardstick, but there are young females present and Mortimer wishes to minimize the amount of time he spends on the gym floor looking like an enginerd. Thus, he uses his rope and determines that the diagonal across the floor is 7'6" longer than the long side of the gymnasium. While the diagonal rope is still stretched tightly across the floor of the gymnasium, Mortimer makes a quick protractor measurement and sees that the rope makes an angle of 62° with respect to the short side of the gymnasium. Make a diagram and compute the area of the gym floor to the nearest square foot.
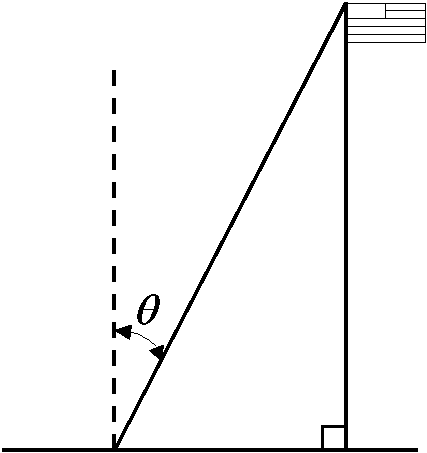
2.
A flag atop a 110-foot flagpole is illuminated by four floodlights that are equidistant from the flagpole’s base. The floodlights are positioned at the vertices of a square, 42 feet on a side, and the ground is flat in the vicinity of the flagpole. Your task is to compute the angle q at which each floodlight must be tipped from the vertical in order to illuminate the flag (see diagram). Is q an angle of elevation? ____ Why or why not? ______________________________ Draw another diagram, in 3 dimensions, and compute q correct to the nearest minute: ____________