Name: ____________________
Names of those to whom you gave help: _______________________
Sketchpad Lab IV
IMPORTANT: Although you should work with a partner (preferably using a separate computer for each person), each student must write his own words and must submit his own lab report. Initial here _______ to certify that you have read this instruction.
1. Open a new sketch.
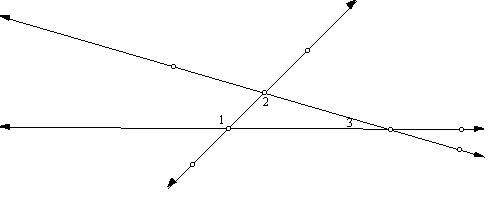
2. Place three lines on your sketch so that they intersect to form a triangle.
3. Arrange them as below, and construct the points of intersection.

4. Measure the angles I have marked 1, 2, 3
Ð 1 = _________ Ð 2 = __________ Ð 3 = ___________
5.
Move the lines a little so that the measures of the angles change.6. Write a conjecture relating the measures of angles 1, 2 and 3.
7. Close, but do not save your sketch.
8. Open a new sketch.
9. Place a line and a point not on that line on your new sketch.
10. Select both the point and the line. Construct a line through the point which is parallel to the first line.
11. Select one point from each of the lines. Construct a line through the two parallel lines. This line will be our transversal for the rest of this part of the lab.
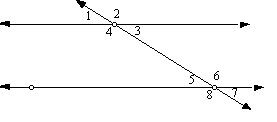
12. Measure all eight of the angles I have labeled.
|
angle |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
measure |
13. Hide the upper of the parallel lines.
Draw a line which crosses your transversal but which is not parallel to the lower line.
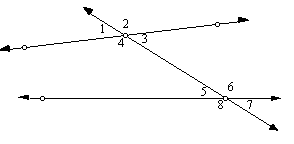
14. Measure all eight of the angles I have labeled.
|
angle |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
measure |
15. Using the correct vocabulary which describes the relative positions of angles (vertical angles, alternate interior angles, alternate exterior angles, interior angles on the same side of the transversal, corresponding angles), explain which angles are congruent when the lines are parallel but are not congruent when the lines are not parallel.
16. Using the correct vocabulary which describes the relative positions of angles (vertical angles, alternate interior angles, alternate exterior angles, interior angles on the same side of the transversal, corresponding angles), explain which angles are congruent whether the lines are or are not parallel.
17. Which angles are supplementary? Write a conjecture. (Remember, a conjecture is a general statement, not a statement about these numbered angles.)