|
Geometry / Mr. Hansen |
Name: _________________________ |
Geometry Sketchpad Lab II
You should work with a partner (but preferably with each person using his own computer).
Each person must write and hand in his own copy of the lab report. Initial here ____ to indicate that you have read this instruction.
You should answer all questions completely, and write complete sentences for all conjectures.
Use the backs of pages, if necessary, to write your explanations.
I. AAA does not guarantee that the triangles are congruent.
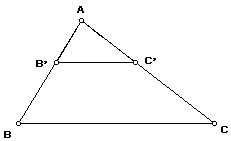
1. Place three points on your sketch, and use
CONSTRUCT, SEGMENT several times to make a triangle. Label vertices so that we may call your triangle DABC.2. Select point A. Go to
TRANSFORM, MARK CENTER A.3. Now, select the entire triangle. Go to
TRANSFORM, DILATE.Type 0.4 for the New Scale Factor. Your drawing should resemble mine.

4. Use Sketchpad to measure these angles:
ÐABC= ______________, ÐAB'C'= _____________
ÐACB = ______________, ÐAC'B'= _____________
5. Measure these segments:
sAB = ___________ sAC = __________ BC = _______________
sAB' = ____________ sAC' = __________ B'C' = ______________
6. Here we have a situation where the three angles of one triangle are congruent to the three angles of another triangle, but the triangles are not congruent.
The corresponding sides of these triangles are not congruent.
Write a conjecture about the ratios of the lengths of the sides of these triangles. Then raise your hand so that I may review your diagram and conjecture.
II. SSA does not guarantee congruence of the triangles.
1. Close the old sketch and do not save it. Open a new sketch.
2. Place three points on your sketch, and label them so that we may call your triangle DABC.
3. Place 3 more points on your sketch, and construct a triangle labeled DEF.
4. Measure
ÐABC, AB and AC, then measure ÐDEF, DE and DF.5. Move points around until you have achieved the following conditions:
Ð
ABC @ Ð DEF , AB = DE, AC = DF and DABC is not congruent to DDEF.Here is my set of triangles: (Your set should not be exactly the same as mine!)
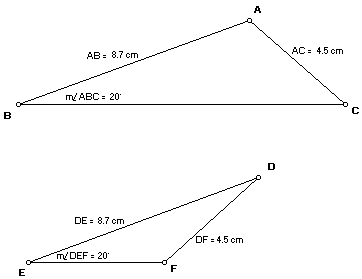
6. When you have your triangles, as required, call me over to see your triangles.
Measure the other two angles of each triangle. Write the measures of the angles here:
m
ÐBAC = _________ mÐACB = ______________mÐEDF = _________ mÐDFE = ______________
7. Here we have a situation where two sides and a non-included angle of one triangle are congruent respectively to two sides and a non-included angle of another triangle, but the triangles are not congruent. The remaining angles of the triangle are not respectively congruent.
Write a conjecture that describes the situation we have here (in general) and how this situation relates to the corresponding angles of the noncongruent triangles that may arise. Then raise your hand so that I may review your diagram and conjecture.
III. Constructing a median and an altitude in a Triangle.
1. Close and do not save your old sketch.
2. Open a new sketch and place an obviously scalene triangle on it.
3. Label your triangle ABC, with A the angle of greatest measure.
4. Construct the midpoint of
sBC and label it D. Construct median sAD.5. Construct the altitude, sAE, from A to sBC.
6. In this space, write a brief set of directions explaining how you constructed the altitude,
sAE.
7. Measure the lengths AB, AC, AE and AD.
AB = ________ , AC = ________ , AD = ________ , AE = ________
8. Now, move your triangle around until it is isosceles, with AB = AC.
Measure
sAE and sAD now. AD = __________ AE = _______________.Write at least two interesting conjectures (or possibly one biconditional conjecture) about the median and altitude from the same vertex in the same triangle. Then raise your hand so that I may review your diagram and conjecture.
IV. Congruence and Area.
1. Close and do not save the old sketch.
2. Construct two triangles on the new sketch. Measure their areas.
3. Move points around so that the two triangles have the same area but are obviously not congruent.
4. If two triangles are congruent, then they will have the same area.
Is this statement true?_________ (explain)
5. Write the converse of the conditional statement in #4.
6. Is the statement you wrote in #5 true? ___________ (explain)