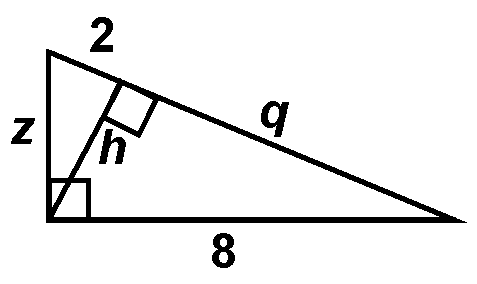
Compute lengths h, z, and q to the nearest hundredth. Do not round too soon!
Solution:
There are many, many ways to work this problem. One way is to start by finding q as follows:
82 = q(q + 2)
64 = q2 + 2q
q2 + 2q – 64 = 0
By quadratic formula (with a = 1, b = 2, and c = –64), we get q = –1 + Ö65 or q = –1 – Ö65. Clearly, the second of these is invalid since a length must be positive. To the nearest hundredth, q = 7.06. However, we retain the full precision of 7.062257748 in our calculator’s memory so that the roundoff errors will not accumulate and contaminate our later answers.
Since the altitude h is the geometric mean between 2 and q, we have 2/h = h/q. Since we know q, we can solve this proportion to get h = 3.76 to the nearest hundredth. Again, though, we retain the full precision of 3.758259637 in our calculator’s memory.
Finally, we use the Pythagorean Theorem on the smallest triangle to obtain 22 + h2 = z2. Since we know h, we can solve for z to get z = 4.26 to the nearest hundredth.