|
1.
|
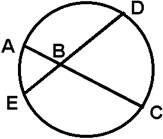
|
Given: AC = 12, AB = 4, EB = 6
Find: ED
|
|
2.
|
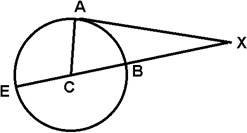
|
Given: circle C has radius 7"
arc
AB = 60°
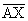 tangent at A tangent at A
Find: all 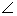 s, arcs, segment lengths, and arc lengths s, arcs, segment lengths, and arc lengths
|
|
3.
|
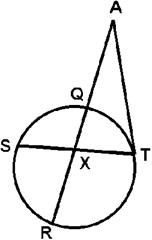
|
Given: 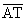 tangent at T tangent at T
arc
QT = 80°
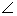 AXT = 70° AXT = 70°
arc
RT = 110°
Find: all 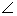 s and arcs s and arcs
|
|
|
|
|
|
|
Answers
(don’t peek until you have tried to solve the problems!)
|
|
|
1.
|
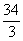
|
Reasoning:
Since BC = 8, (AB)(BC) = 32.
Thus (EB)(BD) = 32 also.
Since EB = 6, BD = 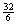 . .
To get ED, use EB + BD as follows:
EB + BD = 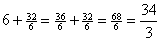 . .
|
|
2.
|
1. AC = BC = EC = 7 in.
2.  CAX = 90° CAX = 90°
3. arc AB = 60°
4. length of arc AB = 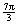 in. in.
5. 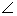 ACB = 60° ACB = 60°
6. 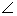 ACE = 120° ACE = 120°
7. arc EA = 120°
8. length of arc AE = 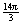 in. in.
9. lower arc EB = 180°
10. length of lower arc EB = 7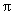 in. in.
11. 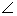 X = 30° X = 30°
12. CX = 14 in.
13. BX = 7 in.
|
Reasons (numbered only for clarity; this is not a proof):
1. Given
2. Radius to pt. of tangency
3. Given
4. 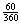 of circumf. = of circumf. = 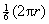 , r = 7 , r = 7
5. Central 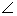
6. Supp.
7. Based on central 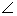 ACE ACE
8. 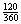 of circumf. (similar
to step 4) of circumf. (similar
to step 4)
9. Semicircle since C is ctr.
10. Half of circumf., circumf. as above
11. Sum to 180°
12. Double AC since 30°-60°-90°

13. Subtr. (CX minus radius)
|
|
3.
|
1. 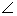 AXT = AXT = 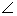 SXR = 70° SXR = 70°
2. 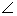 SXQ = SXQ = 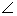 RXT = 110° RXT = 110°
3. arc TR = 110°
4. arc SQ = 110°
5. arc QT = 80°
6. 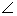 ATX = 95° ATX = 95°
7. 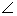 A = 15° A = 15°
8. arc SR = 60°
|
Reasons (numbered only for clarity; this is not a proof):
1. Given, vert. 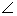
2. Supp., vert. 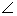
3. Given
4. Must be same since 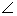 RXT is “Half S” RXT is “Half S”
5. Given
6. Inscr. 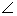 must be must be 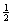 (arc SQT) = (arc SQT) = 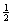 (190°) (190°)
7. 180° in  AXT, or use AXT, or use 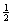 (110° – 80°) (110° – 80°)
8. Use algebra: 70° = 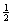 (80° + arc SR). Or,
subtract all known arcs from 360°. (80° + arc SR). Or,
subtract all known arcs from 360°.
|


