Part I.
1.
B (namely, the ^ bisector line)
2.
C (the only point that satisfies this equation is the same as point S in the diagram for #1 in Part II)
Half credit was provided for choice D. Although the equation appears to be the equation of a circle, the locus is a degenerate circle (a single point) since the radius is 0.
3.
E
Reason: If you label angles A and B as both being x° (and they must be, since DABC is isosceles), then exterior ÐC must be 2x°. Bisect to get x° and x°, and voila! You have @ alt. int. Ðs. Since the second locus is a line || to line AB, the locus of intersection is Æ.
Part II.
1.
By inspection (or midpt. formula), S is the point (2, –2). [By an amazing coincidence that one student noticed, this is the same as the locus mentioned in problem #2 of Part I.]
Show work (distance formula) to get CS = Ö37. It is very helpful if you label this as CS, since then I know what you are computing! Since C is 2/3 of the way from A to the opposite side (property of centroids), AS must by 3Ö37.
2.
arc QR (must be 150° by rule of Half SAD, or you can use fact that larger inscribed Ðs must subtend larger arcs)
3.
segment PR (opposite the smallest Ð)
4.
segment QR (the largest possible chord is a diameter; chords get larger as you move closer to the center of the circle, so look for the chord that is opposite the largest Ð)
5.
40° < x < 120°
If you could not get this, try labeling your diagram as follows:
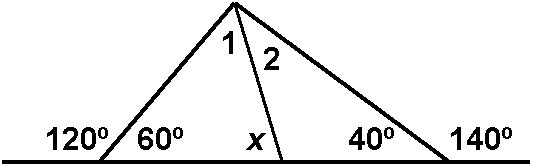
By exterior Ð inequality, x > 40°. (Or, you could say x = Ð2 + 40°. Since Ð2 can be arbitrarily close to 0°, we can conclude that x > 40°.)
By property of Ds, 60° + Ð1 + x = 180° . Simplify this equation to get Ð1 + x = 120°. However, since Ð1 can be arbitrarily close to 0°, we can conclude that x can be arbitrarily close to 120°, though x can never quite equal 120°.
Final answer: 40° < x < 120°
6.
AD < CD < CA < CB < AB
Several students tried to involve DB (which was not requested) in the inequality. It is an interesting fact that in a D of this type, AC < DB for all values of ÐB up to about 38°10'. However, if ÐB ³ 38°11', you can no longer trust your eyes since AC would be longer than DB. Try proving this! It is a great exercise for reviewing your trigonometry.
7.
(x – 2)2 + y2 = 9 [no work required]
8.
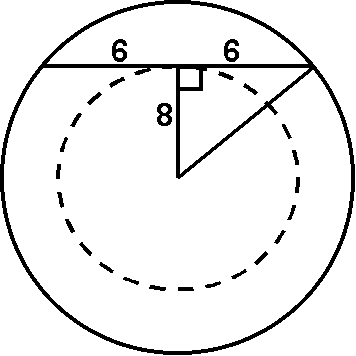
Radius of outer circle is 10 inches. The locus of midpoints is the inner (dotted) circle, which must have radius 8 (6-8-10 D by inspection).
Alocus = pr2 = p(82) = 64p sq. in.
9.
Locus #1 is a line (any line). Locus #2 is a single large concentric circle with radius 12 m. Intersection of Locus #1 with Locus #2 could be Æ, a single point of tangency, or 2 chordal points. Answer: choice a.
10.
This was a fairly hard problem. Most of the students who got it right probably relied on their intuition, which in this case was accurate.
If the centroid and the circumcenter coincide, then each median is guaranteed to have not just one but two points in common with each ^ bisector (namely, the midpoint of the opposite side, and the centroid). Therefore, the medians and the ^ bisectors must coincide. That is a defining property of isosceles Ds. But since all 3 medians coincide with all 3 ^ bisectors, our D must be isosceles for all 3 bases. Answer: choice a (equilateral).
11.
segment AE
Reason: Segment BD is the shortest in DBCD, but in DBDE, segment BE must be even shorter. Looking finally at DABE, although BE is small, AE must be even smaller.
12.
C (equidistant implies 3 congruent radii reaching back to that point)
13.
B (occurs only if the triangle is obtuse)
14.
B (since the orthocenter is directly on the rt. Ð vertex, its distance is 0)
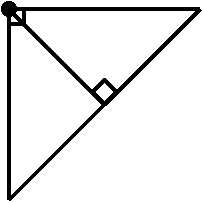
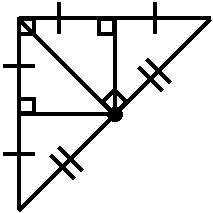
(note that in this case, the circumcenter is on the hypotenuse)
Part III (Proof).
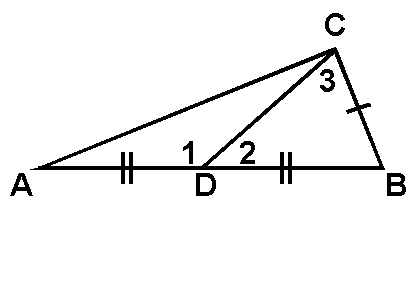
1. DB > BC
2. mÐ3 > mÐ2
3. mÐ1 > mÐ3
4. mÐ1 > mÐ2
5. sCD @ sCD
6. sAD @ sDB
7. AC > BC
1. Given
2. Larger Ð opp. larger side
3. (DCBD) ext. Ð exceeds rem. int.
4. Trans.
5. Refl.
6. Given
7. Hinge Thm. (steps 4,5,6)
Q.E.D.
Alternate method (very clever, found by a student in B period):
Since DB > BC (given), BC is not the longest side in DCBD. Therefore, Ð2 must be acute, since if Ð2 were either right or obtuse, BC would be opp. the largest Ð in DCBD and hence the longest side. But if Ð2 is acute, Ð1 must be obtuse, and we can apply Hinge Thm. to conclude AC > BC, since AD = DB (given) and CD = CD (refl.)—Q.E.D.
Many students tried to assert that mÐ1 > mÐ2 by diagram (or by omission of steps), but remember that you cannot assume that. The diagram might not be drawn to scale.