Part I (6 points): Choose the one best answer.
A) two parallel lines
B) a line
C) a point
D) a circle
E) Æ
1. ___
What is the locus of points in a plane that are equidistant from two given points?
2. ___
What is the locus of points in the xy-plane that satisfy the equation (x – 2)2 + (y + 2)2 = 0?
3. ___
- What is the locus of points that are on line AB, and on the line that contains the the bisector of the exterior angle at C?
Part II (35 points): Answer each question in the space provided. If calculations are required, show your work for full credit.
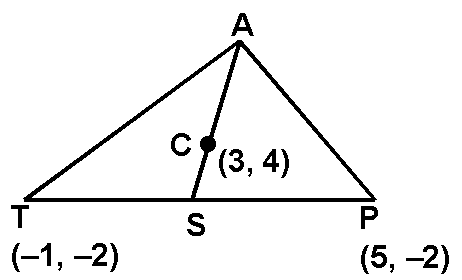
1.
If C is the centroid of DATP, find length AS.
The diagram at right applies to questions 2-4. 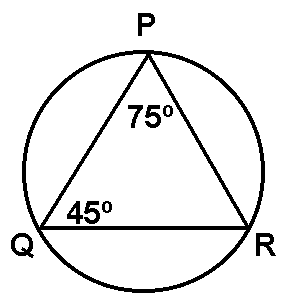
2.
Which arc (arc PQ, arc PR, or arc QR) is the longest?
3.
Which side of D PQR is the shortest?
4.
Which chord is closest to the center of the circle?
5.
Find the range of possible values for x.
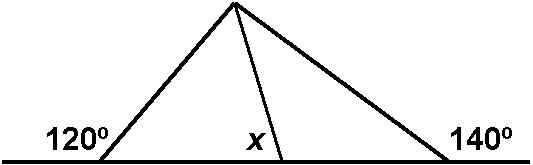
6.
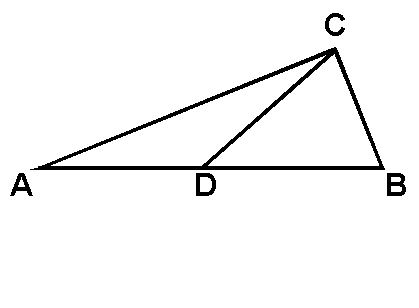
Write an inequality that expresses lengths CA, CD, CB, AD, and AB in order from shortest to longest.
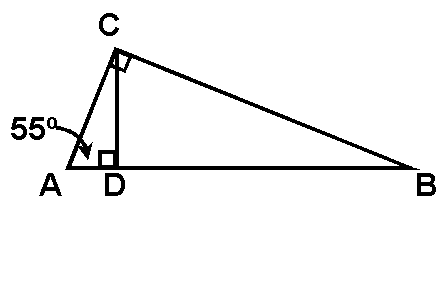
7.
Write the equation of the locus of points in the xy-plane that are 3 units from (2, 0).
8.
In a circle with radius of length 10 inches, all possible 12-inch chords are drawn. Find the area of the locus of the midpoints of all such chords.
9.
* This question refers to a compound locus in a plane.
The locus of points that lie on a given line and that are 7 meters from a circle with a diameter of 10 meters is:
a) 0, 1, or 2 points
b) 0 or 2 points
c) 0, 1, 2, or 3 points
d) 0, 2, or 3 points
e) 0, 1, or 2 points, or a line
10.
If the centroid and the circumcenter of a triangle are located at the same point, then the triangle is
a) equilateral
b) isosceles but not equilateral
c) scalene
d) could be a, b, or c
e) can never happen
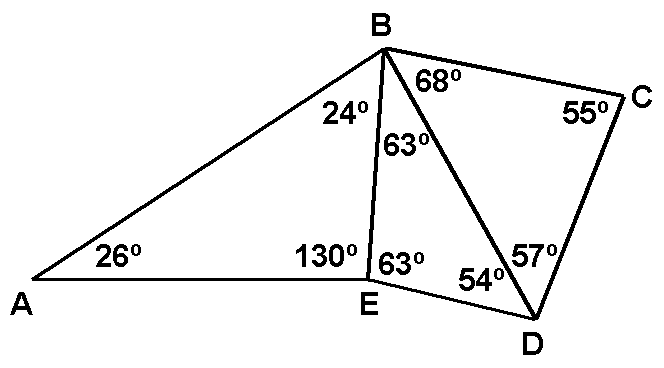
11.
Find the shortest segment in the diagram.
In problems 12-14, choose the one best answer:
a) an incenter
b) an orthocenter
c) a circumcenter
d) a centroid
12.
Which of the points named above is equidistant from the vertices of a triangle?
13.
Which of the points named above could be outside a circumscribed circle of a triangle?
14.
In an isosceles right triangle, which of the points named above is closest to the right angle’s vertex? Support your answer with four sketches.
a) Incenter sketch
b) Orthocenter sketch
c) Circumcenter sketch
d) Centroid sketch




Part III (9 points): Provide a two-column proof.
Given: AD = DB, DB > BC
Prove: AC > BC