1.
Solve the following system. Give answers in exact, reduced ratio form (not decimal approximations).
3x – 2y = 5
2x + 4y = 8
2.
Given the indicated points on line l, find A and B using exact, reduced ratios.
Note: Diagram is not necessarily to scale.
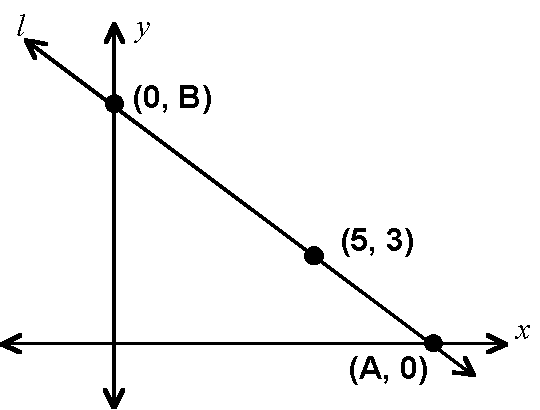
3.
Find the center and radius:
x2 + y2 – 6x + 4y = 36
4(a).
Describe the shaded region with an inequality
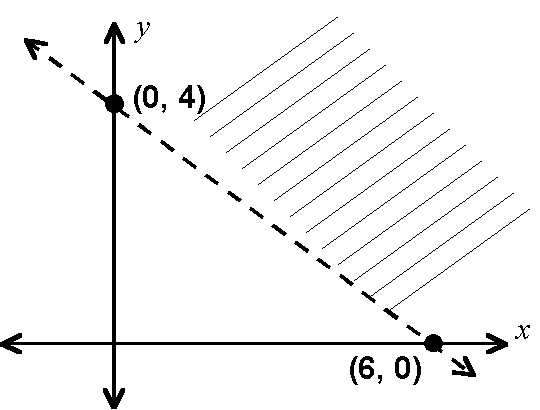
4(b).
Describe the shaded region with a system of inequalities.
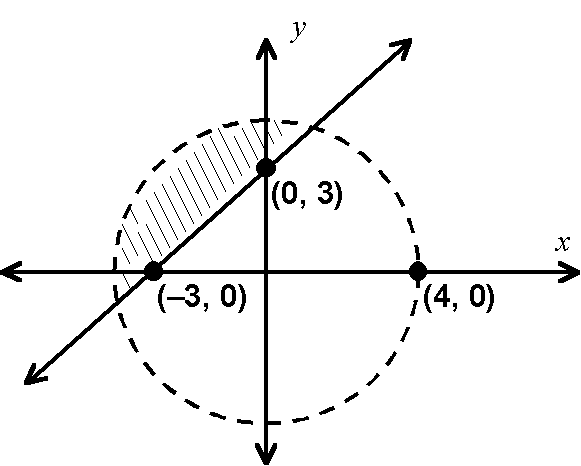
5.
There are two lines that have a y-intercept of (0, –6) and form a 30° angle with the x-axis. Find equations for these lines. Give all numbers in exact form.
6.
Using the "box method," placing one of the corners of your box at the origin, plot the point (3, 4, –5).
7.
A regular square pyramid has vertices at (3, 0, 0), (0, 3, 0), (–3, 0, 0), (0, –3, 0), and (0, 0, 4). [Note: These coordinates were different in different sections of the class.] Find each of the following:
(a)
the volume of the pyramid
(b)
the length of a lateral edge
(c)
the total surface area, using exact values
8.
Consider the following points: A(–5, –4), B(2, 5), C(7, 0).
(a)
Plot the points and draw DABC.
(b)
What are the coordinates of the midpoint of segment AC?
(c)
What is the length of the median from B to segment AC?
(d)
What is an equation of the line containing the altitude from B to segment AC?
(e)
What is the length of the altitude from B to segment AC?
(f)
What is the area of DABC?