Geometry / Mr. Hansen
4/22/2002

Name: ________________________

Chapter 12 Review (p. 597)

 17.

V_desired = V_block – V_cylinder
          = lwh_block – ßh_cylinder
          = (8)(5)(6) – p(1²)(8)
          = 240 – 8p
          » 215 cu. in.

20.

Sketch circle O with sector AOB:

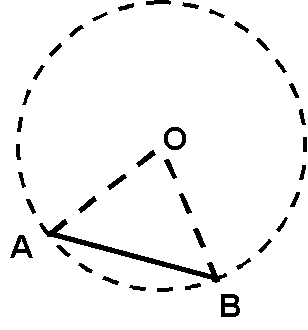
Do you see that circular segment AB (i.e., the sliver that equals sector AOB minus DAOB) is the cross section of the log?

Since central ÐO = 60° and ÐA @ ÐB (base Ðs of isosc. D), DAOB is equilateral with area s²(Ö3)/4 = 10²(Ö3)/4 = 25Ö3.

A_{segment AB} = A_{sector AOB} – A_DAOB
             = (60/360)pr² – 25Ö3
             = (1/6)p10² – 25Ö3
             = 100p/6 – 25Ö3

Note here that we used the fact that r = 10, which follows from the cross-section diagram above.

Because the log is an extruded shape (i.e., a generalized cylinder),
V_log = ßh
      = (A_{segment AB}) h
      = (100p/6 – 25Ö3) (30)
      = 3000p/6 – 750Ö3
      = 500p – 750Ö3 cu. units

TSA_log = A_{front cap} + A_{back cap} + A_{flat top} + A_{curved bottom}
          = A_{segment AB} + A_{segment AB} + (10 · 30) + (60/360)LSA_cylinder
          = 2(100p/6 – 25Ö3) + 300 + (1/6) Ch
          = 200p/6 – 50Ö3 + 300 + (1/6)(20p)(30)
          = 200p/6 – 50Ö3 + 300 + 600p/6
          = 800p/6 – 50Ö3 + 300
          = (400p/3 – 50Ö3 + 300) sq. units

Again, note that the circumference C uses the fact that the log has diameter 20, which is clear from the cross-section diagram above.

21.

The trick is to extend the cone upward to apex A:

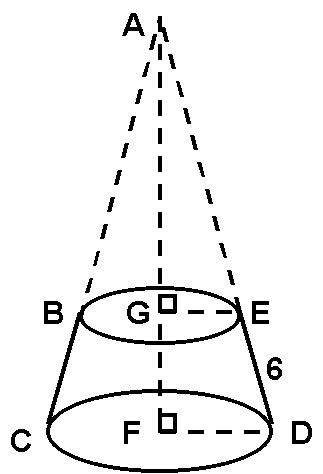
By similar Ds, ratio GE : FD is the same as ratio AG : AF (be careful not to say AG : GF). But that is also the same as AE : AD (be careful not to say AE : ED).

Let AE = x. Then x/(x + 6) = GE/FD = 9/12. Solving gives
12x = 9(x + 6)
12x = 9x + 54
3x = 54
x = 18

If AD = 24 and FD = 12, then by inspection, rt. Ds AGE and AFD are not only similar but also 30°-60°-90°. (You wouldn’t necessarily have this, but it’s helpful to notice that it happens in this particular problem.) Thus AG = 9Ö3, AF = 12Ö3.

V_frustum = V_{cone ACD} – V_{cone ABE}
          = (1/3)ß_bigh_big – (1/3)ß_smallh_small
          = (1/3)(p12²)(12Ö3) – (1/3)(p9²)(9Ö3)
          = (1728p/3)(Ö3) – (729p/3)(Ö3)
          = (576p)(Ö3) – (243p)(Ö3)
          = 333pÖ3 cu. units

22.(a)

The given triangle is 30°-60°-90° with hypotenuse 8. Thus the short leg is 4, and when spun, the figure makes a cone with slant height 8, radius 4, and height 4Ö3.

V_cone = (1/3)ßh
       = (1/3)(p4²)(4Ö3)
       = (64/3)(pÖ3) cu. units

(b)

When spun, the figure forms a tube with outer radius 4 and inner radius 3 (i.e., a short pipe with walls of thickness 1, outer diameter 8, and inner diameter 6).

Another way to think about this is as a large cylinder with a cylindrical hole removed from its center.

V_desired = V_{outer cyl.} – V_{inner cyl.}
          = ß_outerh – ß_innerh
          = (p4²)(5) – (p3²)(5)
          = 80p – 45p
          = 35p cu. units