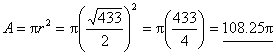|
|
Selection: #1-5 all, 7, 8, 12, 14, 17, 18, 19, 20, 23, 24, 25, 26a.
Note: In most cases, you would be required to furnish some work, or at least
leave a “trail” so that partial credit could be awarded in the event of a
stumble that throws all the later answers off. Most of the explanations here
are omitted or abbreviated.
|
|
1.
|
a. 94°
b. 94°
c. 43°
|
|
2.
|
x = 66°
y = 32°
|
|
3.
|
a. BE = 12, so BD = 16
b. (PT)2 = 4(4 + 12), so PT = 8
c. 3(15) = 5(SW) 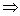 SW = 9 SW = 9 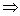 XW = 4 XW = 4
|
|
4.
|
a. 13 (by inspection since 5-12-13 rt.  ) )
b. 8.5 (by inspection since 8-15-17 rt.  with diameter as
hypotenuse) with diameter as
hypotenuse)
c. 7 (by inspection since 7-24-25 rt.  ) )
|
|
5.
|
125
Reason: 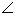 P is 55° by the
“Half A” rule. But then minor arc WX must be 125° by the “ice cream cone” theorem (TTT). P is 55° by the
“Half A” rule. But then minor arc WX must be 125° by the “ice cream cone” theorem (TTT).
|
|
7.
|
a. Since circumference is 2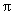 r = 2 r = 2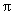 (6) = 12 (6) = 12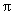 cm, and since 45° is 45/360 or 1/8 of a full circle, arc length
of arc XY is 12 cm, and since 45° is 45/360 or 1/8 of a full circle, arc length
of arc XY is 12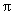 )/8 = )/8 = 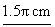 . .
b. Take answer to part (a) and add XO + OY = 6 + 6. Final answer: 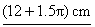 . .
|
|
8.
|
a. We did this in class on 3/5/02 (B, C, and D periods). Easiest method is
to let x = radius of circle A. Mark T as the point of tangency between
A and B, U the point of tangency between B and C, and V the point of tangency
between C and A. Then mark AT and AV as x, BT and BU as 7 – x,
and CU and CV as 11 – x. It is clear from examining segment BC that
the marked portions must add up to 10. In other words, BU + CU = (7 – x)
+ (11 – x) = 10. Solve to get 18 – 2x = 10, or x = 4.
b. By inspection, radius of circle B is 7 – x = 3, and radius of
circle C is 11 – x = 7. C is the largest circle.
|
|
12.
|
We must have a rectangle, 4 by 7.5. Hypotenuse (diagonal) is 8.5 by
inspection (8-15-17 pattern), and since that hypotenuse is also a diameter
(as proved by the inscribed rt. 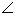 ), radius is 4.25. ), radius is 4.25.
|
|
14.
|
Note typo in text (found by E. Longosz): there
should be a segment bar, not an arc symbol, over AB.
Standard trick for all external tangent situations: drop  from P to from P to 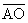 and call the point
of intersection X, so that ABPX is a rectangle. Then BP = AX = 2, OX = 6, and and call the point
of intersection X, so that ABPX is a rectangle. Then BP = AX = 2, OX = 6, and
 OXP is a 6-?-10 rt. OXP is a 6-?-10 rt.  where the longer leg
XP is unknown. By inspection, XP = 8 since this is a 3-4-5 pattern, and AB
= 8 also. where the longer leg
XP is unknown. By inspection, XP = 8 since this is a 3-4-5 pattern, and AB
= 8 also.
|
|
17.
|
Mark arcs (in order) as x, 2x, 5x, and 4x,
where x is some unknown quantity. Since x + 2x + 5x
+ 4x = 360°, x must be
30°. Now remove the mystery and
re-mark the arcs as 30°, 60°, 150°,
and 120°.
Mark point A as the vertex between the 30°
and 60° arcs, B as the vertex between
the 60° and 150° arcs, C as the vertex between the 150° and 120°
arcs, and D as the remaining vertex. By the “Half A” rule, inscribed 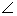 s A, B, C, and D must be 135°, 75°,
45°, and 105°, respectively. s A, B, C, and D must be 135°, 75°,
45°, and 105°, respectively.
|
|
18.
|
a. 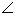 X = 140°
(by TTT) X = 140°
(by TTT)
b. 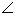 Y = ˝ (90° – 30°) = 30° (by “Half D” rule) Y = ˝ (90° – 30°) = 30° (by “Half D” rule)
c. 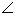 Z = 10°
by subtracting from 180° (or by “Half
D” rule) Z = 10°
by subtracting from 180° (or by “Half
D” rule)
|
|
19.
|
Let B be the point where ray QO intersects circle O. Then
(TP)2 = 5(5 + QB)
225 = 25 + 5QB
200 = 5QB
QB = 40
r = QO = 20
|
|
20.
|
Let x = meas. of arc AB, y = meas. of arc CD.
Clearly x + y = 160, since that’s how many degrees are left over after
accounting for arcs AD and BC.
By “Half D” rule, m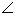 P = 30 = (x – y)/2, so 60 = x – y. P = 30 = (x – y)/2, so 60 = x – y.
Combine this with prev. equation to get a system:
x + y = 160
x – y = 60
Solve to get x = meas. of arc AB = 110,
y = meas. of arc CD = 50.
|
|
23.
|
By tangent-secant power thm.,
102 = 5(5 + x + 9)
100 = 5(14 + x)
100 = 70 + 5x
30 = 5x
x = 6
By chord-chord power thm.,
9x = 3y
9(6) = 3y
54 = 3y
y = 18
|
|
24.
|
By distance formula,
d = 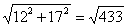 , but we do not bother to simplify (you’ll see why) , but we do not bother to simplify (you’ll see why)
r = 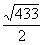
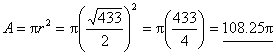
Do you see why it would have been a waste of time to evaluate or simplify 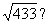 We end up squaring a
moment later anyway. We end up squaring a
moment later anyway.
|
|
25.
|
Make a diagram. Let r = radius
of small circle, R = radius of
large circle. Half the chord (40 cm) makes a rt. 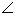 with the 9 cm radius
of small circle. Hypotenuse is 41 since (9, 40, 41)
is a Pythagorean triple, though you would be forgiven for not knowing that.
But hypotenuse = R, so
circumference = with the 9 cm radius
of small circle. Hypotenuse is 41 since (9, 40, 41)
is a Pythagorean triple, though you would be forgiven for not knowing that.
But hypotenuse = R, so
circumference = 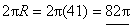 . .
|
|
26a.
|
Regular hexagon: 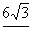 after chasing around
30°-60°-90° triangles and using the fact that a
regular hexagon can be subdivided into 6 congruent equilateral triangles. after chasing around
30°-60°-90° triangles and using the fact that a
regular hexagon can be subdivided into 6 congruent equilateral triangles.
Square: 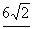 after making use of
45°-45°-90° facts. after making use of
45°-45°-90° facts.
Equilateral triangle: 6 after making liberal use of 30°-60°-90° triangles.
|