1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

d [Error in text! Problem must clarify that Ð2 and Ð3 are the base angles.]
b
c
c
d
a, c [Probably another misprint: (c) should have said DKPF @ DMPF.]
S
S
A
A
A
N

13.

1. Circles R and S (given)
2. RA = RB (radii are @)
3. SA = SB (same reason)
4. RS = RS (reflexive)
5. DRAS @ DRBS (SSS, steps 2, 3, 4)
6. ÐARC @ ÐBRC (CPCTC)
7. RC = RC (reflexive)
8. DARC @ DBRC (SAS, steps 2, 6, 7)
9. AC = BC (CPCTC)
10. sRC is a median to sAB (def. median)

14.

r = 2

15.

–2 < x < 6

16.

x = –2 [note: 3 does not work]
perimeter = 4 + 5 + 6 = 15

17.

1/11
The 11 possibilities are 1,1,22; 2,2,20; 3,3,18; and so on through 11,11,2.

18.

The two dotted right triangles have their right angles at (2,11) and (9,4), which we may call A and B, respectively. By inspection, AM = WB = 3, and AR = RB = 7. Since ÐA and ÐB are both right Ðs (hence @ ), we have DARM @ DBRW by SAS. Thus RM = RW by CPCTC, so DMRW is isosceles.

[A briefer sketch of this proof would be acceptable.]

19.

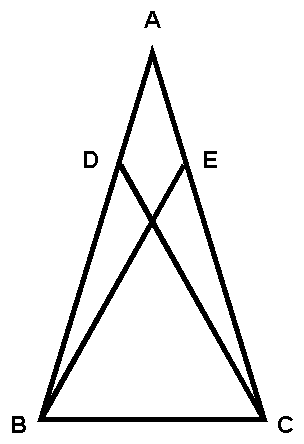
Given: DABC is isosceles, with AB = AC
           AD = AE
Prove: CD = BE

1. AB = AC (given)
2. AD = AE (given)
3. DB = EC (subtr. prop.)
4. ÐDBC @ ÐECB (base Ð s of isosc. DABC)
5. BC = BC (reflexive)
6. DDBC @ DECB (SAS, steps 3, 4, 5)
7. CD = BE (CPCTC)

20.

Since PF and PC are radii, they are equal in length. Since PA = PD (given), AF = DC by subtraction. But then AC = DF by addition, and BC = FE (given), so that right triangles ABC and DEF are congruent by HL. Finally, ÐC @ ÐF by CPCTC.

Practice 1

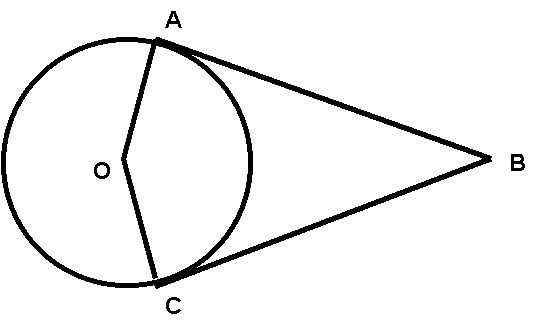
Given: circle O
           sOA ^ sAB
           sOC ^ sCB
Prove: sAB @ sBC

1. circle O (given)
2. sOA ^ sAB, sOC ^ sCB (given)
3. OA = OC (radii are @)
4. draw dotted segment from O to B (2 pts. determine a line)
5. OB = OB (reflexive)
6. ÐOAB, ÐOCB are rt. Ðs (def. ^)
7. DOAB @ DOCB (HL, steps 6, 5, 3)
8. sAB @ sBC (CPCTC)

Sam Empson’s clever alternate version:
1. circle O (given)
2. sOA ^ sAB, sOC ^ sCB (given)
3. OA = OC (radii are @)
4. draw dotted segment from A to C (2 pts. determine a line)
5. ÐOAC @ ÐOCA (base Ðs of isosc. DOAC)
6. ÐCAB compl. ÐOAC, ÐACB compl. ÐOCA (def. ^, def. compl.)
7. ÐCAB @ ÐACB (compls. of @ Ðs are @)
8. sAB @ sBC (isosc. Û base Ðs @)

Practice 2 (tepee problem)

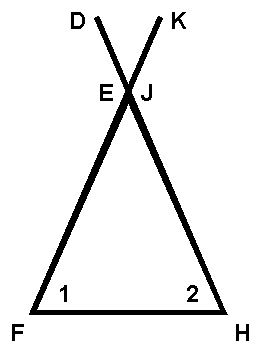
Given: Ð 1 @ Ð 2
           DH = KF
Prove: DE = KJ

1. Ð1 @ Ð2 (given)
2. EF = JH (base Ðs @ Û isosc.)
3. DH = KF (given)
4. DE = KJ (subtr. prop.)