|
W 1/2/13
|
Classes resume.
|
|
|
Th
1/3/13
|
HW due: Write #7.27, 7.28,
7.29c, 7.40, 7.42 on pp. 383-385. Note:
#7.42 is referring to the scoring scheme that formerly applied to the AP
exam, though there were 40 questions instead of 50.
|
|
|
F 1/4/13
|
HW due: Write #7.43 on p.
385. For parts (a) and (b), show the full work, table and all. Then, use your
calculator to check your work, and breathe a sigh of relief (aaaaaaahhhhh!). Work is required for parts (c) through
(f), too, but if you are clever, you can shorten up the time considerably.
|
|
|
M 1/7/13
|
HW due:
1. Write #7.41 on p. 385. For part (e), let us assume that both distributions
are normal. You should therefore compute the probability that a peg is too
big to fit in the predrilled hole.
2. Continue reading, as always. Make sure you are especially familiar with
the material on pp. 386-394.
|
|
|
T 1/8/13
|
HW due: Write #7.45, 7.47, 7.46,
7.50, 7.53, 7.54. Please do the problems in the order indicated.
|
|
|
W 1/9/13
|
HW due:
1. Correct your class notes to say that the variance of a geometric random
variable X is Var(X) = q/p2, not p/q2.
The online source we tapped yesterday had an error! (There’s a life lesson in
there someplace . . .)
2. Write #7.60 on p. 396, then #7.64, 7.70, 7.72, and 7.76 on pp. 412-414.
|
|
|
Th
1/10/13
|
HW due: Read the paragraphs
below, and write 35 minutes’ worth of review problems (your choice) from Chapters
1-7.
For each problem, indicate the page
number, the problem number, and
your complete solution. If you
cannot solve the problem, then write a list of specific questions that you need to know in order to tackle the
problem. For example, a “specific question” related to #7.52 on p. 395 would
be, “Is the table on p. 831 showing pdf entries or cdf entries?” A bad question to ask (no credit for this)
would be, “I don’t understand #7.52. How do I do it?”
Note: This is a good start on your
midterm exam preparation.
For §7.6, the only thing you are responsible for is understanding and
interpreting normal probability plots, a.k.a. normal quantile
plots, such as those on p. 416. If the NQP is straight or nearly straight,
the data set is approximately normal. If the NQP shows a bend to the left as
you travel from left to right (as in Figure 7.37(a) on p. 416), the data set
is skew left. If the NQP bends to the right, the data set is skew right. If
the NQP is twisted in the shape of the graph y = x3, as
in Figure 7.37(b), then the data set has heavy tails.
In class: Review.
|
|
|
F 1/11/13
|
HW due:
Locate your Barron’s (or equivalent) AP review book and bring it to class.
Numerous other publishers have books that are of similar scope and quality,
but the Barron’s book is the one that will be used as the source for midterm
exam questions. Bring both the review book and your regular textbook to
class. No additional written work is due, but previously assigned problems
may be scanned a second time. In particular, make sure that you have finished
#7.64, 7.70, 7.72, and 7.76 on pp. 412-414.
In class: Review.
|
|
|
M 1/14/13
|
Midterm Exam, 8:00–10:00 a.m., MH-315. Format will be similar to an AP exam, only shorter.
Many problems will be drawn from the Barron’s review book, with possible
modifications. Scoring will be on an “AP curve.” You will have a standard set
of AP formula sheets available for your use during the exam. A graphing
calculator is required, and spare batteries are strongly recommended.
The exact tables and formula sheets you will be provided with are on pp.
12-18 of this resource:
http://apcentral.collegeboard.com/apc/public/repository/ap-statistics-course-description.pdf
Note! If you print these, be aware that the printed page numbers are actually
wrong. When sending the document to a printer, you should request pages
16-22. The reason for the discrepancy is that there are 4 unnumbered pages at
the beginning of the PDF file.
|
|
|
W 1/23/13
|
Classes resume.
|
|
|
Th
1/24/13
|
No additional written work
is due. Continue with your daily reading, as always.
|
|
|
F 1/25/13
|
HW due: Write #8.2, 8.3, 8.4 on pp. 449-450.
|
|
|
M 1/28/13
|
HW due: Write #8.10, 8.11,
8.11bc (see below), 8.12, 8.13abcd (see below), 8.14abc (see below), 8.16.
8.11(b) What model should we use,
if not the z model, for the
sampling distributions given in #8.10 that you did not list in #8.11?
8.11(c) Would it be correct or incorrect to use the model you stated in
#8.11(b) for all 6 of the situations listed in #8.10? Explain.
8.13(d) If the population has extreme skewness, how would your answer to #8.13(c) change? Would the
probability increase, decrease, or stay the same? Explain briefly.
8.14(c) Describe the shape of the sampling distribution of 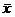 in #8.14(a). in #8.14(a).
|
|
|
T 1/29/13
|
No additional written work
is due. Continue with your daily reading, as always.
|
|
|
W 1/30/13
|
HW due:
1. Correct your 1/28 HW by comparing against the answer key below. Use a
different color of ink (blue or green recommended), and be prepared to state
what you learned, if anything, from each mistake. If you wish to write out
your “lessons learned” as a sentence on your HW paper, so much the better.
8.10(a) 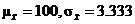
(b) 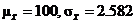
(c) 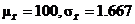
(d) 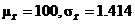
(e) 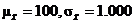
(f) 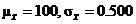
8.11 The sampling
distrib. of 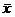 is reasonably normal
for parts (c) through (f), where n
= 36, 50, 100, or 400, as long as the population does not have extreme skewness or extreme outliers. is reasonably normal
for parts (c) through (f), where n
= 36, 50, 100, or 400, as long as the population does not have extreme skewness or extreme outliers.
(b) For n = 9 and n = 15 (parts (a) and (b)), we could use the t distribution as a model of the sampling distribution IF WE KNOW THAT THE UNDERLYING
DISTRIBUTION IS NORMAL.
(c) It would be
correct to use the t model for
parts (a) and (b) IF WE KNOW THAT THE
UNDERLYING DISTRIBUTION IS NORMAL. For parts (c) through (f), the t model is also correct, regardless of
whether or not the underlying distribution is normal. In fact, the t distribution is preferable to the z distribution for modeling the sampling
distribution of 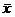 . The reason is that in the real world, . The reason is that in the real world, 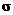 would not be known,
and we should use the t model instead of the z model when would not be known,
and we should use the t model instead of the z model when 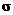 is unknown,
regardless of sample size. is unknown,
regardless of sample size.
8.12 The
population consists of data having a mean of 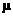 and a s.d. of and a s.d. of 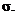 The symbols The symbols 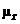 and and 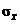 refer to the mean
and s.d. of the sampling
distribution, not the underlying data distribution. refer to the mean
and s.d. of the sampling
distribution, not the underlying data distribution.
8.13(a) 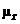 = = 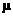 = 40, = 40, 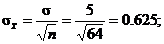 the sampling distrib. of the sampling distrib. of 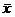 is approx. N(40, 0.625) is approx. N(40, 0.625)
(b) 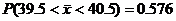 by calc. [use normalcdf, but don’t write that down!] by calc. [use normalcdf, but don’t write that down!]
(c) 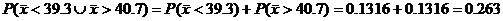
(d) Extreme skewness (lack of
normality) could mean more probability in the tails than the z model would predict. Result: The
answer to part (c) might increase, but not necessarily, since the increase in
probability on one side might be counterbalanced by a decrease on the other.
8.14(a) 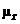 = = 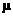 = 0.5, = 0.5, 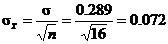
(b) 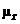 = = 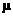 = 0.5, = 0.5, 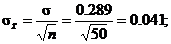 shape would be
approximately normal since n is
large [you need to make a sketch] shape would be
approximately normal since n is
large [you need to make a sketch]
(c) In (a), the sampling
distribution is not normal, because
n is not large. The sampling
distribution would be somewhere in between the uniform shape of the
underlying data distribution and the normal shape that the CLT tells us is
approached as n grows large.
8.16(a) 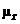 = = 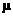 = 150 lbs. = 150 lbs.
(b) 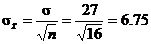
(c) Since 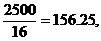 having having 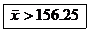 would cause a problem would cause a problem
(d) 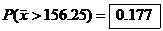 by calc. by calc.
2. Write #8.22 on p. 461.
3. Write #8.28 on p. 467.
|
|
|
Th
1/31/13
|
HW due:
1. Make sure that #8.22 and #8.28 are in reasonably acceptable condition. Use
nearby odd-numbered problems, if necessary, as a way of reverse engineering
the specific skills you need to answer #8.22 and #8.28. You should not count
this time toward your 35-minute time log target, since this is merely doing
what you should have done yesterday.
2. Write #8.30 on p. 467.
3. Write #8.31 on p. 467, with the addition of parts (c) and (d) as shown
below.
(c) Compute the probability of a Type II error in part (a).
(d) Compute the probability of a Type II error in part (b).
4. Write #8.36 on p. 470.
|
|