|
Th
11/1/012
|
HW due: Bring your worked questions to class on a fresh sheet of paper. You can
rehash old problems, or (better yet) choose some new problems, but regardless
of what you do, you must use a fresh sheet of paper. Your textbook contains
hundreds of problems, many with answers in the back of the book. Choose at
least a few problems that you cannot solve. During class, we will cover as
many of your unsolved problems as time permits. Your homework will be graded
based on the quality of your work, including your “stumper questions.” See
examples below.
Example of a “zero effort, zero
credit” writeup of a stumper question:
#4.23 on p. 168
?
Example of a bad writeup
of a stumper question (bad because the student has still made no effort):
#4.23 on p. 168
I have no idea what the question is asking. What is the “2 standard
deviations rule”?
Example of a better (though still
weak) writeup of a stumper question:
#4.23 on p. 168
n = 27
s = 610.743
2s = 1221.49
I don’t know what to do with this. What does the “2 standard deviations rule”
mean?
Example of a strong writeup in which the student is still partially stumped:
#4.23 on p. 168
n = 27
s = 606.894
2s = 1213.788
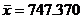
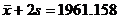
Q2 = 750
Q2 + 2s
= 1963.788
I don’t know whether to choose $1.961 million or $1.964 million as my answer.
Does it matter?
|
|
|
F 11/2/012
|
Big Quiz
(30 minutes, 60 points) on all material from the year to date. You are responsible for all terminology and notation
presented in the book and/or discussed in class, all textbook material and
assigned exercises through p. 237 (end of §5.3), and the additional in-class
discussions of Type I/Type II error, PPV, P-value,
and null and alternative hypotheses.
A problem similar to #6.68 on p. 334, which was assigned for HW due Oct. 3,
is likely to be on the quiz, as are the terms sensitivity and specificity.
(Sensitivity is the probability of avoiding a false negative, given that the
subject has the condition or disease being tested. Specificity is the
probability of avoiding a false positive, given that the subject does not have the condition or disease
being tested.) Note: In #6.68, the
helpful hint of making a tree diagram was provided. You, however, will be given
no such hint. You simply have to know that a tree diagram is what you need.
Another problem of the same type is #6.74 on p. 335. Again, however, be aware
that the step-by-step helpful hints provided in #6.74 will not be given to you on the Big Quiz.
|
|
|
M 11/5/012
|
HW due: Sleep! Also, continue with your daily
reading, and get caught up on previously assigned problems that you may have
been unable to finish because of lime limitations. There are no additional
problems due (other than those that were previously assigned, that is).
|
|
|
T 11/6/012
|
HW due: Review the starred questions on the Must-Pass Quiz. Begin with the end
in mind!
|
|
|
W 11/7/012
|
(The day after Election Day.) No additional HW is
due today, so that you have the option of watching the election returns if
you wish.
In class: A quiz on the starred questions from the Must-Pass Quiz is possible.
|
|
|
Th
11/8/012
|
HW due: Sleep!
|
|
|
F 11/9/012
|
No school (teacher
workday).
|
|
|
M 11/12/012
|
HW due: Write #5.52 and
#5.54 on pp. 252-253.
An audit of your reading notes is also possible today. If you have none, that
is acceptable, but then you may be subject to an oral reading check of the
type described in class. For example, you could be asked if there was an
example in the text concerning NBA player salaries. The answer is yes [see p.
174], and if you had read the text, you would surely remember that, as well
as at least one of the team names for which boxplots
were shown.
If your reading notes are reasonably complete, you will not be subjected to
an oral reading check.
|
|
|
T 11/13/012
|
HW due:
1. Pick a personal number between 1.2 and 1.9 that has 2 decimal places after
the decimal point. An example would be 1.83. Call your number p, since it will become the exponent
for a power function.
2. Make a table of x and y values for x from 1 to 4, with a step size of 0.25. That gives you a total
of 13 x values. Your y values should be computed by the
formula y = xp.
3. Make a third column that introduces some random noise into your y data. Generate a random value using
the rand function (MATH PRB 1 ENTER), subtract 1, multiply the result by x, and add that quantity to the existing
value of y. Label this third column
as ynoisy.
4. What transformation could you “hit” ynoisy with so that
you could get back to something close to a linear relationship between the x column and the ynoisy column?
5. Perform the transformation you proposed in #4, and find the LSRL that best
fits the scatterplot of x as explanatory variable and that transformed ynoisy
as response variable. Label the transformed ynoisy as T. Therefore, your LSRL should look
like 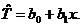
6. “Undo” the transformation by performing its inverse on both sides of your
LSRL from #5. Your final result should be an equation that gives an estimate
for 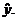
7. Run all of your original x
values through the “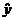 function machine”
you found in #6. Subtract these values from their corresponding ynoisy
values to get a set of 13 residuals. function machine”
you found in #6. Subtract these values from their corresponding ynoisy
values to get a set of 13 residuals.
8. Make a residual plot of x values
on the x-axis and the entries from
#7 on the y-axis. What can you
conclude?
|
|
|
W 11/14/012
|
HW due:
1. Prepare for an open-notes quiz on this
week’s Quick Study article.
2. Continue with your daily reading, as always. A reading check is possible.
|
|
|
Th
11/15/012
|
HW due:
1. Finish Tuesday’s assignment if you have not already done so.
2. Write #5.57.
3. Use algebra to write an equation for your final, overall prediction of 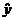 as a function of x. In effect, you already did
something similar to this when you answered part (e). as a function of x. In effect, you already did
something similar to this when you answered part (e).
Note: As you are doing your daily
reading, you may skip pp. 255-263.
|
|
|
F 11/16/012
|
NOTE: Class today will meet in MH-103.
HW due: Write up your solution to the following problem.
Yesterday, in class, we proved that if the “true” underlying relationship
between x and y, before the addition of noise, is exponential, then there is a
linear relationship between x and
log y. After we find that linear
relationship, using our superior LSRL skills, we can use a little bit of
algebra to write an equation for 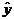 as an exponential function of x, namely as an exponential function of x, namely 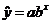 for suitable constants a and b. WE DID ALL OF THAT.
CHECK YOUR NOTES TO MAKE SURE YOU UNDERSTAND WHAT WE DID. for suitable constants a and b. WE DID ALL OF THAT.
CHECK YOUR NOTES TO MAKE SURE YOU UNDERSTAND WHAT WE DID.
Your goal for today is to prove that if the “true” underlying relationship
between x and y, before the addition of noise, is a power function, then there
is a linear relationship between log x
and log y. In other words, show
that if we hit both the explanatory
variable column and the response variable column with a log, then the linear
relationship between log x and log y allows us to reconstruct a power
function, 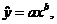 for suitable
constants a and
b. for suitable
constants a and
b.
Note that your calculator performs these steps when you request STAT CALC ExpReg or STAT CALC PwrReg. The
r value stated is the linear correlation
coefficient for the transformed linear fit, not for the original data set.
|
|
|
M 11/19/012
|
HW due: Be prepared for an
open-notes quiz on the Simpson’s Paradox video. You
may watch the video as many times as you wish.
In class: Guest speaker, Mr. Joe Morris ’62, MITRE Corporation.
|
|
|
T 11/20/012
|
No additional written HW is
due. Continue your daily reading, as always. Nobody has visited for extra help
concerning the assignment that was due last Friday, and that means that it
could reasonably be collected and graded for correctness. Right?
|
|
|
W 11/21/012
|
Thanksgiving break begins.
|
|
|
M 11/26/012
|
Classes resume.
HW due: Bring in an actual clipping (not a Web printout) of a relatively
recent newspaper or magazine article that describes a statistical
controversy. If your parents will not allow you to clip the article, you may
bring in the entire newspaper section or magazine in which the article
appeared. If you have no newspaper or magazine subscriptions, then find a
recent newspaper or magazine in someone’s recycling bin.
As we discussed in class last Tuesday, this will not be an article that
merely includes statistics or contains a footnote concerning how different
data items may have been tabulated, since those are commonplace. A successful
article will be one in which the statistical controversy is the subject of
the article, front and center. Two examples that you cannot use (since we
already discussed them) are these:
(1) the article in the Monday 11/19 issue of The Washington Post concerning GWU’s unranked status in the
USN&WR rankings following revelations that GWU’s “% of incoming class in
the top 10% of their high school graduating class” statistic was incorrect,
and
(2) the article in the Monday 11/19 issue of The Washington Post concerning likely cheating by DCPS principals
and teachers in order to make their schools’ standardized test results look
better.
The second article was particularly relevant to our class, because the
article included a discussion of a standard of proof, namely the point at
which we should regard the number of erased and re-bubbled answers to be so
large as to make chance alone an implausible explanation.
|
|
|
T 11/27/012
|
HW due: Write #5.72 on p.
271. Use of PC-based or Internet-based graphing software is optional, since
your graphing calculator will work just fine. You will need 4 scatterplots (labeled properly, of course) in part (a),
and you must show your work and provide at least a sentence of explanation in
part (b).
|
|
|
W 11/28/012
|
HW due: Write #5.52, 5.54,
5.57, and 5.60. The first 3 have already been assigned, and you do not need
to do them a second time if they were complete and correct the first time.
For #5.60, use your recommended transformation to perform the following
additional required steps:
(a) Write an equation for your predictor function.
(b) Use the result of part (a) to estimate canal length for a seal that is
3.5 years old.
(c) Use the result of part (a) to estimate age when canal length is 175 mm.
|
|
|
Th
11/29/012
|
HW due: Write #6.1, 6.2,
6.4, 6.10, 6.14, 6.22.
|
|
|
F 11/30/012
|
HW due: Write #6.28 through
6.40 even on pp. 310-313, plus the following problem.
Problem: I have 3 piles of coins,
NN, QQ, and mixed. NN means 2 nickels, QQ means 2 quarters, and “mixed” means
one of each type of coin. I scramble the coin piles and select a coin at
random. What is the probability that the other coin in that pile is a
quarter, given that I chose a nickel? In other words, what is P(Q2
| N1)?
|
|