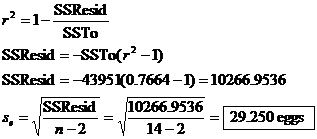|
M 10/1/012
|
No additional written
HW due. Continue reading, as always.
|
|
|
T 10/2/012
|
HW due: Write #3.40 on
pp. 125-126.
|
|
|
W 10/3/012
|
HW due:
1. Read this
week’s Quick Study and be prepared for an open-notes quiz. Only
handwritten notes are permitted. Typed notes, photocopies, etc. are not
allowed.
2. Write #6.68abcd on p. 334. You will probably need to refer to your class
notes.
|
|
|
Th
10/4/012
|
HW due:
Each group must submit a research
question and a brief
methodological proposal for our upcoming group project on exploratory
data analysis. If the group leader is absent today for any reason, a deputy
must deliver the assignment at class time.
Example:
Research question
Do left-handers, as compared to right-handers, show
any unusual patterns of answers when they take a multiple-choice quiz
involving questions that require a large amount of guessing?
Proposed
methodology
We will recruit 15 left-handers and 15 right-handers
from among our friends (a convenience sample). We will not tell any of the
subjects what we are looking for. All subjects will give us some basic
demographic data (age in months, number of siblings, number
of cars in household) and will take the same 20-question multiple-choice quiz
(choices A/B/C/D for each question). All subjects will be instructed not to
leave any questions blank. Only 5 of the questions will be easy enough that a
high school student of average skill would be expected to know the answer,
and those will be sprinkled among mostly much harder questions. We will
compute, for each group, the sample mean and sample s.d.
of the scores, as well as the 5-number summaries. We will display the
5-number results with comparative boxplots. We will
then analyze the numbers of A, B, C, and D responses
among each group, for each question, and will prepare illustrative graphs. We
will also characterize the types of patterns seen, if possible, and attempt
to see if there are systematic differences between the groups. For example,
it is possible that most of the right-handers follow a strategy of
consistently guessing with the same letter, while most of the left-handers
follow a strategy of cycling through A, B, C, and D on successive hard
questions. Finally, we will compute correlation coefficients between all
possible pairings of the following quantitative variables, both separately
(for each handedness group) and in the aggregate: quiz score, age, number of
siblings, and number of cars in household.
|
|
|
F 10/5/012
|
No school (faculty professional day).
|
|
|
M 10/8/012
|
No school (Columbus Day).
|
|
|
T 10/9/012
|
HW due:
1. Write #3.30 on p. 116.
2. Each group must submit a revised research question and methodology
proposal, taking into account the suggestions made last week. If the group
leader is absent for any reason, a deputy must submit the document. List all
group member names, with the group leader’s name underlined. It is
most helpful if names are in the upper right corner of the first page.
3. This time, include a proposed schedule of milestones with your group
submission. Milestone dates should include, at a minimum, the following:
date(s) for gathering data, date by which analysis will be complete, and date
by which final report will be submitted to Mr. Hansen for grading. You are
strongly encouraged to add a milestone for submitting a draft for
suggestions. (NO ROUGH DRAFTS, PLEASE.
Those are a waste of everyone’s time. However, a meeting of one or more group
members with Mr. Hansen to discuss project direction is certainly
acceptable.)
|
|
|
W 10/10/012
|
HW due:
1. Read this
article from yesterday’s New York
Times. Pay special attention to the scatterplot,
and answer the following questions in writing:
(a) What are the explanatory and response variables? Be careful, especially
for the response variable.
(b) Estimate the values of x and y from the axes, and enter the data
into lists L1 and L2 on your calculator. Give the
equation of the LSRL, as well as the linear correlation coefficient and the
sample size. Use correct notation throughout.
(c) Is the general trend linear? Give both evidence to support a “yes” answer
and evidence to support a “no” answer, and then make a decision based on your
own judgment. Be sure to include a residual plot.
(d) Based on the LSRL you obtained in part (c), compute the value of 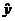 when x = 1.0. Show your work.
(e) State the value of the slope (b1),
and interpret the slope in the context of this model.
(f) Does the LSRL model predict a victory for Mr. Obama or for Mr. Romney?
Explain briefly.
2. Read this
article from The Washington Post,
and be prepared for an open-notes quiz. Notes must be handwritten.
|
|
|
Th
10/11/012
|
No additional written HW is due today. Continue
reading and making reading notes, as always.
|
|
|
F 10/12/012
|
HW due: Write #4.14 on p. 159, #5.22 on p. 219, and
#5.36 on p. 234.
|
|
|
M 10/15/012
|
HW due: Write #2.46 on p. 55, #3.20 on p. 95, and
#3.38 on p. 125. Complete sentences are expected in your answer to #3.38d.
|
|
|
T 10/16/012
|
No additional written HW is due today. Continue
reading and making reading notes, as always.
|
|
|
W 10/17/012
|
HW due:
1. Read this
week’s Quick Study article, and be prepared for an open-notes quiz on it.
2. Copy the notational translation table from the 9/30/2010 calendar entry into your
notebook. Henceforth, you should use 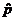 (not p) for all HW problems that request a
sample proportion, and p (not 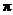 ) for all HW problems that request a population proportion
(i.e., long-run relative frequency).
3. What single word do we usually use to mean long-run relative frequency?
Write the answer on your HW paper, labeled as question #3.
4. Write #4.4, 4.6, 4.10, and 4.12 on pp. 157-159.
|
|
|
Th
10/18/012
|
HW due: Write #4.16, 4.19 (using your own words to explain
parts b and c), 4.20, 4.21, 4.24, and 4.28 on pp. 166-169.
|
|
|
F 10/19/012
|
HW due: Because the headmaster’s announcement at
lunch on Thursday 10/18 implied that the web server was down, many students
may have assumed that they would be unable to reach this site tonight. If you
are reading this message, you are surely aware that it is only the e-mail
server that is down, not the web server. However, because of the possible
confusion associated with the announcement, there will be no additional written
HW due today. Please use the time to get caught up on previously assigned
problems or, if you are already caught up, to sleep. Continue reading at your
normal pace, of course.
Note: We could have had some written homework due today, since nothing is
wrong with the web server. You should always check here, regardless of any
other announcements or rumors you may have heard. However, on this particular
occasion, Mr. Hansen the Merciful made the decision to have a night with no
additional HW.
|
|
|
M 10/22/012
|
HW due:
1. Write #4.32 on p. 175. Be sure to give a reason for your answer to part
(a).
2. Write #4.33 on pp. 175-176.
3. The 11 confidence intervals we gathered last Friday for the size of the
2012 AP Statistics exam cohort are given below. All values are in thousands.
[5, 900]
[5, 100]
[1, 75]
[0.6, 50]
[20, 30]
[1, 150]
[20, 800]
[10, 500]
[200, 300]
[15, 200]
[0.5, 80]
(a) Compute the mean, s.d., and 5-number summary
for the lower endpoints of the intervals. Label all values with proper
notation in your answers to this and all other questions.
(b) Compute the mean, s.d., and 5-number summary
for the upper endpoints of the intervals.
(c) Compute, for each student, a point estimate as the mean of the upper and
lower endpoints. For example, the point estimate for student 1 would be
452,500. Then compute the mean, s.d., and 5-number
summary of these 11 point estimates.
(d) Discuss the relationship among 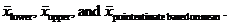 Hint:
Look for patterns, and explain what is going on.
(e) Compute, for each student, an alternate point estimate as the geometric
mean of the upper and lower endpoints. For example, the point estimate for
student 1 would be 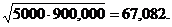 Then compute the mean, s.d., and 5-number summary of the 11 point estimates you
obtained in this alternate way.
(f) Plot comparative modified boxplots for the
5-number summaries you found in parts (c) and (e).
(g) The true value, which you can easily verify here,
is 152,750. How many of the 11 students captured the true value with their
confidence intervals?
(h) Give an example of a value that falls within more students’ confidence
interval estimates than the true value did. How many students found the value
that you named to be “acceptable” (i.e., contained within their confidence
intervals)?
(i) Which “Delphi” method of polling the students
seems to show the best promise for prediction: using point estimates based on
conventional means, using point estimates based on geometric means, or
looking for values that are “acceptable” to the largest number of students?
Explain your reasoning.
(j) What can we conclude about the students’ claim that their confidence
intervals were 90% confidence intervals?
|
|
|
T 10/23/012
|
HW due: Write #4.36, 4.40, and 4.48 on pp. 183-185,
and answer the additional question below.
A1. In your own words, write a
functional definition of a z
statistic. In other words, what is it
that a z score is attempting to
measure? Try to answer this without referring to your notes. In class, we
will compare answers and will learn a little bit from each slightly wrong
attempt.
|
|
|
W 10/24/012
|
HW due: Write #4.60 on p. 194 and #5.2, 5.3, 5.4,
5.8, and 5.12 on pp. 208-210.
|
|
|
Th
10/25/012
|
HW due: Write #5.16 on p. 210 and #5.26, 5.28, 5.30,
and 5.34 on pp. 219-221.
|
|
|
F 10/26/012
|
HW due: Write #5.38, 5.40, and 5.42 on pp. 234-235.
|
|
|
M 10/29/012
|
No school (Hurricane Sandy).
|
|
|
T 10/30/012
|
No school (Hurricane Sandy).
|
|
|
W 10/31/012
|
HW due: Write #5.44 and 5.46 on pp. 236-237, and
copy the following solution to #5.42(b) into your HW paper for last Friday. SSTo, SSResid, and se are not required for the
AP exam, but you should be able to read a textbook. After all, you will be
doing that a lot in college, and this course covers college-level material.
5.42(b) Since r2 =
0.7664 and SSto = 43951, we have
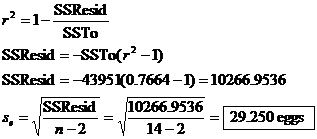
Interpretation of se:
Roughly speaking, the number of eggs in a typical clutch differs by about 29
from the quantity predicted by the LSRL, where the LSRL gives predicted
clutch size as a function of snout-vent length.
|
|