|
W 9/5/012
|
First day of class.
|
|
|
Th
9/6/012
|
HW due:
1. Start reading your textbook. We will eventually cover essentially the
entire book through p. 747, so you might as well start reading it now! That works
out to an average of 5 pages per school day, which is manageable, but only if
you keep up. In class today, we will discuss exactly what the expectations
for reading and note-taking are.
2. Send Mr. Hansen an e-mail message. Remember to put a double underscore ( __ ) at the start of your subject line.
|
|
|
F 9/7/012
|
HW due:
1. Numerous people must have sent messages without a double underscore ( __ )
in the subject line, because I did not receive 13. Please check your “Sent
Mail” folder, and re-send if necessary with the proper subject line.
2. Grade each of the following entries from yesterday’s quiz on a scale of 0
to 2 points, where 0 = completely or almost completely incorrect, 1 = almost
correct, 2 = fully correct. The question, as you recall, was to give an
example of a statistic. Be prepared to defend the score that you assign.
(a) Number of flights I took with Lufthansa in 2011.
(b) Percentage of the STA Upper School student body present at Upper School
lunch on 9/5/012.
(c) Field goal % of the Washington Wizards’ 2011 NBA season. [Presumably he
meant 2011-12.]
(d) Number of students in Sam’s Bar from the time period 9:00 AM – 9:10 AM on
a Tuesday.
(e) The amount of money the STA bookstore made each day in the 2011-12 school
year.
(f) The final grades of all the students that took calculus in the 2011-12
school year at STA.
(g) The third quarter grades of all the students
that took calculus in the 2011-12 school year at STA.
(h) The word count for the book War and
Peace.
(i) The kill to death ratio for [name] in one game
of Call of Duty.
(j) The average free-throw percentage of [name] over a certain 5-game span in
2011.
(k) Number of words in my Am Lit essay on Huckleberry
Finn from the first semester of the 2011-12 school year.
(l) Bryce Harper’s batting average through the first 100 games this season.
(m) The % of answers to this question which are in fact statistics.
3. For part (a) through part (m) in #2, write the correct symbol, an equal
sign, and a reasonable guess at the value of the statistic. If you awarded a
score of 0, skip and move on to the next one. If you awarded a score of 1,
make your best guess at what statistic the student had in mind. The first one
is done for you as an example. Note:
We do not use the “approximately equal” sign (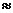 ) in our class, since probably half the numbers we look at
are approximations anyway. ) in our class, since probably half the numbers we look at
are approximations anyway.
(a) n = 4
|
|
|
M 9/10/012
|
HW due:
1. Continue reading in your textbook. Your goal is a minimum of 25 pages per
week, or 5 pages per school night. Try to read ahead, especially during the
early part of the year, since the material is not too hard yet.
2. Gather a set of at least 20 numeric data points, and enter them into list
L1 on your calculator. Keep a written record of the entries. (Use
a standard HW sheet as described here.) Then
produce
(a) a stemplot (as demonstrated in class last
Friday),
(b) the sample mean, written as an equation with correct notation for the
symbol,
(c) the sample s.d., written as an equation with
correct notation for the symbol,
(d) the 5-number summary.
For parts (b), (c), and (d), you are encouraged to use the 1-Var Stats
feature of your calculator (STAT CALC 1), which was demonstrated in class
last Friday.
As to the matter of where you should gather data, the answer is . . . be creative! You could measure your own height 20 times to
the nearest millimeter, and the answers will vary slightly. Or, you could ask
20 friends for the number of TVs they have in their house. Or, you could ask
20 NCS girls to measure their right pinky fingers. If you are lazy, you could
even flip a coin 20 times and let your data be a stream of values where 0 =
head, 1 = tail.
On Monday, we will look at your data and will try to guess where the data
came from. A couple of bonus points will be awarded to the most interesting
data set, as judged by Mr. Hansen.
|
|
|
T 9/11/012
|
HW due: No additional written
work is due today. However, continue reading in the textbook, as always.
|
|
|
W 9/12/012
|
HW due: Write Activity 1.3 on p. 24, #1.27 on p. 25.
Continue reading as always.
|
|
|
Th
9/13/012
|
HW due: No additional written
work is due today. However, continue reading in the textbook, as always.
|
|
|
F 9/14/012
|
HW due: Write #1.20,
1.23, 2.1, 2.8. This assignment will be collected Monday, since there is no
class today (Form VI retreat).
|
|
|
M 9/17/012
|
HW due: Write #2.12,
2.14, 2.20, 2.24. Be sure you know all the boldface terms on pp. 33-39.
|
|
|
T 9/18/012
|
HW due: Read this
current article and this
older article from The Washington
Post, and be prepared to discuss both articles in the context of recent
textbook pages. Older HW assignments may also be re-checked, so you should
use this as an opportunity to get caught up.
|
|
|
W 9/19/012
|
HW due: Write #2.32,
2.45, 2.50. Continue reading, as always.
|
|
|
Th
9/20/012
|
HW due: Write #2.58,
2.66, 2.68. Continue reading, as always.
|
|
|
F 9/21/012
|
No additional written
HW due. Continue reading, as always, but please enjoy the weather and experience
a feeling of awe.
|
|
|
M 9/24/012
|
HW due: Start working
on the following review problems. All you have to show for today is evidence
that you made a solid start. These problems are due in full on Tuesday. You
may write directly on printouts of the old tests if you wish.
1. Work through this old practice test.
Omit question 17, and for questions 18-20, provide only a sketch and an estimated answer.
2. Do these problems as well.
Omit questions 25 and 26. The answer to #23 is “regression outlier,” which is
something we have not discussed yet but which you should know for the test. A
regression outlier is not
determined by the 1.5 IQR rule; the 1.5 IQR rule is only for univariate data. Since we have bivariate
data in this example, the rule for determining a regression outlier (as opposed to a regular outlier) is that a
regression outlier is something that appears, in your judgment, to be “far
above or far below the regression line.”
3. According to the Washington Post
article about musicians and their ability to process auditory information,
the amount of practice was ________________ associated (hint: provide an adverb ending in -ly)
with the amount of deterioration of hearing ability that normally occurs with
aging. Was the study an experiment? If not, what was it? How do you know?
|
|
|
T 9/25/012
|
HW due:
Finish your review problems.
If you promise not to peek until after
you have done the work, you can look at the answer
key to the Judge Jeremy problems (section #2 in yesterday’s calendar
entry). Note: If you look at the
answer key before challenging yourself and committing yourself to answers you
believe are correct, you are not getting the full benefit. You might as well
use the index to find a worked example in the textbook and simply read
through it. If that actually worked, you wouldn’t need to take a statistics
course; you could simply read a hundred or so carefully chosen examples,
which might take you a week or two, and then you’d be finished with
introductory statistics.
In class: review.
|
|
|
W 9/26/012
|
Test (100 pts.) on everything covered so far.
All textbook reading in Chapters 1 and 2, including examples, is fair game
for the test. The basic content of
the two assigned Washington Post
readings is also fair game. Note that some topics from Chapters 3 and 4 are
also represented in the review problems above, but these should not give you
as much trouble, since we have discussed those topics in class.
The test will be closed notes, with graphing calculator required. If you
forget your calculator, or if your batteries die during the test, there will
be a significant point penalty. Pencil is strongly encouraged, but pen (blue
or black ink) will also be accepted.
|
|
|
Th
9/27/012
|
HW due: Continue
reading in the textbook. No additional written work is due.
|
|
|
F 9/28/012
|
HW due: Read this
week’s Quick Study and be prepared to discuss it. Continue your daily
textbook reading, as always.
|
|