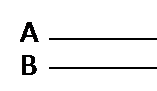|
W 9/5/012
|
First day of class.
|
|
|
Th
9/6/012
|
HW due:
1. Order the textbook (ISBN 0131848283).
2. Send Mr. Hansen an e-mail message. Remember to put a double underscore ( __ ) at the start of your subject line.
|
|
|
F 9/7/012
|
HW due:
1. Someone must have sent a message without a double underscore ( __ ) in the
subject line, because I did not receive 3. Please check your “Sent Mail”
folder, and re-send if necessary with the proper subject line.
2. On a piece of paper, write down several random hex addition problems. Show
your work (including the carries). Then check your answers for accuracy by
using the Windows calculator in “programmer” mode.
|
|
|
M 9/10/012
|
HW due:
1. Be prepared to demonstrate that you are a MOHA (master of hex addition).
2. Do at least half a dozen “thousands complement” problems. Show your work, and check your answers
with a calculator. Show how you sometimes rewrite the problem to use the
complement, and show how and where you sometimes discard the thousands digit.
Perform a mixture of addition and subtraction problems, problems that have
overflow and those that do not, and problems that have or do not have
negative numbers in them.
Question: What negative number is indicated by 737?
Answer: Take the complement, which is 263. Answer:
–263 is the “true” meaning in our usual system of writing numbers.
|
|
|
T 9/11/012
|
No class.
|
|
|
W 9/12/012
|
Perform each of the following subtractions in hex (using
two’s complement arithmetic) as well as decimal. Try to do everything without
the programmer’s calculator, but you can check your work at the end. Show
work, especially the way in which you are rewriting the addends and
deciphering the final answers.
0x31
−0x1A
0x51
−0x7E
0x310C
−0x18B4
0x310C
−0x68B4
|
|
|
Th
9/13/012
|
Perform the following operations in hex, using two’s
complement arithmetic. Check your results, and document your checking in writing.
Be very clear. This is not a difficult exercise, but you need to do your work
clearly, so that it communicates your knowledge. Use a style similar to what
was demonstrated in class yesterday. You may substitute alternate problems if
you do not like these.
0x78
+0x3F
0x51DB
−0x6C39
0x52AC108E
−0x64B04AF2
|
|
|
F 9/14/012
|
Form IV retreat (no class).
|
|
|
M 9/17/012
|
HW due:
1. Draw signal lines for A and B, like this:
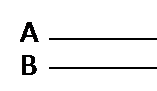
Now, make a circuit diagram flowing from left to right to illustrate the
following expression:
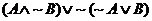
Hint: Although you start with lines
only for A and B, you are allowed to “tap off” extra copies of the A and B
signal as many times as you wish. For example, if you need another copy of A,
just do this:

A solid circle denotes a connection. Wires that cross without a dot are not
connected.
2. Regardless of whether or not you were able to make the diagram requested
in #1, prove that the expression can be simplified to 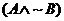 . .
In other words, prove that regardless of the values of A and B (each of which
could be either 0 or 1), the expression 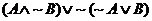 is equivalent to is equivalent to 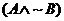 by itself.
“Equivalent” means “having the same truth value.” Show your work clearly, so
that it makes sense to a reader. Chicken-scratching and cryptic work are not acceptable. However, a truth table with a
written conclusion is acceptable. by itself.
“Equivalent” means “having the same truth value.” Show your work clearly, so
that it makes sense to a reader. Chicken-scratching and cryptic work are not acceptable. However, a truth table with a
written conclusion is acceptable.
3. Show how it is possible to construct AND, OR, and NOT gates using only NOR
gates. You are allowed to use as many NORs as you wish, connected in various
creative ways, but NORs are the only
type of gate you may use for this exercise. Prove that your gates work as
required. Truth tables are preferred. If you do not wish to use truth tables
for your proofs, then write clear,
grammatically correct sentences in which you describe the 4 cases that
need to be checked for A and B (true-true, true-false, false-true, and
true-true) and describe exactly how you can tell that the results are the
same for your NOR-type circuits as they would be using “primitive” AND, OR,
and NOT gates.
4. Yes or no: Are there any digital (binary) logic operations that cannot be
performed using AND, OR , and NOT gates?
5. There are 4 possible ways that inputs A and B can be configured
(true-true, true-false, false-true, and false-false). How many well-defined
logic gates are possible for 2 inputs?
|
|
|
T 9/18/012
|
No class.
|
|
|
W 9/19/012
|
HW due: Write answers to the following questions.
1. Explain why the NXOR (a.k.a. XNOR) gate is sometimes called the EQU gate.
Think a little bit before answering; don’t just write the first thing that
pops into your head.
2. Using AND, OR, and NOT gates only, make a “black box” that works exactly
like an XOR gate. After you have finished and tested your black box (show
your testing work!), label your black box with the 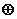 symbol. symbol.
3. Using your 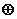 symbol as if it were
a gate in its own right (which it is!), and using AND gates, make a circuit
that can add 2 2-bit binary numbers and return a 3 digit result. Hint: If you label your inputs as C
and A for the most significant and least significant bit of the first number,
and D and B for the most significant and least significant bit of the second
number, then the rightmost bit of the answer is A symbol as if it were
a gate in its own right (which it is!), and using AND gates, make a circuit
that can add 2 2-bit binary numbers and return a 3 digit result. Hint: If you label your inputs as C
and A for the most significant and least significant bit of the first number,
and D and B for the most significant and least significant bit of the second
number, then the rightmost bit of the answer is A 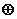 B, with a carry bit of
A AND B. The carry bit is combined with the result of C B, with a carry bit of
A AND B. The carry bit is combined with the result of C 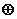 D to produce the
middle bit of the answer, and the carry bit (if any) becomes the leftmost bit
of the answer. A fully correct solution is difficult, but
see if you can make some partial progress on this problem! Think of
how amazed the first people who performed binary addition using digital logic
must have been. D to produce the
middle bit of the answer, and the carry bit (if any) becomes the leftmost bit
of the answer. A fully correct solution is difficult, but
see if you can make some partial progress on this problem! Think of
how amazed the first people who performed binary addition using digital logic
must have been.
|
|
|
Th
9/20/012
|
HW due: Complete #3 from yesterday’s problem set.
Verify that all 16 possible input patterns produce the correct output
pattern.
|
|
|
F 9/21/012
|
HW due: Use a truth table to prove the distributive
laws for ANDs and ORs, namely
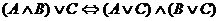
and
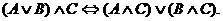
The symbol 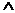 means AND, and the
symbol means AND, and the
symbol 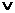 means OR. If you
prefer, you can use the centered dot ( means OR. If you
prefer, you can use the centered dot ( ) for AND and the plus sign (+)
for OR. ) for AND and the plus sign (+)
for OR.
|
|
|
M 9/24/012
|
HW due: Start working
on the following review problems. All you have to show for today is evidence that
you made a solid start. These problems are due in full on Wednesday.
1. From this
old practice test, do problems 3, 5, 6, 8, 9, 10, 11, 13, and 17 only.
For #13, you need to know that “bpp” means “bits
per pixel.” In other words, each pixel of the image is represented by a
number that is stored in 8 bits, and that number represents the color choice
used for that pixel.
2.(a) Simplify the following messy expression to the
greatest degree possible. Then use a truth table to prove that your answer is
equivalent to what you started with.
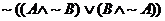
(b) What kind of gate could you use to replace the
messy expression in (a)?
(c) Make a circuit diagram for the messy expression
in A just as it stands, with no simplification.
(d) Using NAND gates only, re-diagram the expression
in (a).
(e) Test all 4 necessary cases (11, 10, 01, and 00)
for A and B to verify that your answer to (d) is correct.
3. Devise a steganographic encoding system for the
following message:
MODD IS COOL
(a) Describe how your system works.
(b) Show how the message above is encoded.
(c) Encode a different secret message of your choice, and give it to someone
else (first without the key you wrote in part (a), then with the key) to see
if he or she can successfully decode your message.
4. What is steganography? Can you pronounce it? Can
you spell it? (Please say yes.)
5. Who was Alan Turing? Mark Zbikowski? (Brief
answers are acceptable. You may have to Google to get the second one, but you
are supposed to already know the first one.)
6. Essay question: Is mathematics a branch of computer science, or is it the
other way around? What do you think? Write a paragraph (4-5 sentences).
7. What percentage of modern electronic technology can be built with AND, OR,
and NOT logic alone? Note: This
assumes that accurate timing pulses are already furnished.
|
|
|
T 9/25/012
|
No class.
|
|
|
W 9/26/012
|
HW due:
Finish your review problems.
In class: review.
|
|
|
Th
9/27/012
|
Test (100 pts.) on everything covered so far.
|
|
|
F 9/28/012
|
HW due:
Perform the following additions in hex. Then interpret the answer as a
decimal (base 10) value. Show your work as you multiply out the place values.
(Warning: Be on the alert for
overflow, and remember that your answer may need to be interpreted as a negative
number.)
Additional requirement: In addition to
giving the answers in hex, translate all values (addends as well as the
answers) into base 10, showing negative numbers where appropriate. That will
also give you a check on your work.
8ACC
+AE84
______
0818
+7FED
______
242D
+9C0F
______
|
|