|
W 5/1/13
|
Giant Quiz II (50 points).
Format will be 9 MC without calculator, 1 FR without calculator, total of 33
minutes (49.5 for extended time).
|
|
|
Th
5/2/13
|
Giant Quiz III (50 points).
Format will be 6 MC with calculator, 1 FR with calculator, total of 33
minutes (49.5 for extended time).
Here are the answers to the FR problem from yesterday’s Giant Quiz II:
(a)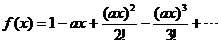 
(b) You were supposed to recognize the pattern of “something to the power of n, divided by n factorial,” which is the familiar Maclaurin
series pattern for exp(something). Answer: f (x) = exp(–ax) or, if
you prefer, f (x) = e–ax.
(c) To find the number of terms needed to guarantee an absolute error of less
than 0.001 when a = 2 and x = 0.2, you can use either the
Lagrange error bound or the AST error bound, your choice. Adequate
justification is needed, of course. Either way, you discover that the first
term that is guaranteed to be less than 0.001 in absolute value is the term
involving n = 5, which means that
you can add up the series through the term for n = 4 and will be secure in the knowledge that the |tail| is less
than 0.001. So, it sounds as if the answer is 4, right? Wrong. The series
begins with the term for n = 0.
Therefore, the correct answer is that you need to take 5 terms. Now,
as it turns out, if you use your calculator or a spreadsheet to see precisely
where the absolute error first drops below 0.001, you’ll see that you
actually achieve that after 4 nonzero terms (i.e., after adding up the terms
through n = 3), as shown in part
(a). However, except for rare situations, the questions on the AP will ask
about the guaranteed convergence,
i.e., the theoretical error bound, not the actual error performance. If you
wrote 4 as your answer, Mr. Hansen will probably score you as RAWR (right
answer, wrong reason), depending on the work you furnished.
Numerous students got confused and thought that a was the center of the
expansion. No, a
was simply a parameter tossed in to make the problem a little more
interesting. The problem clearly stated that the power series was to be
centered about 0.
|
|
|
F 5/3/13
|
HW due: Continue working on
your AP review logsheet.
|
|
|
M 5/6/13
|
HW due: Continue working on
your AP review logsheet.
|
|
|
T 5/7/13
|
HW due: Continue working on
your AP review logsheet.
Karl found a multiple-choice
demo video that he said was extremely helpful.
|
|
|
W 5/8/13
|
AP Examination, 7:45 a.m., Trapier
Theater. Bring several sharpened
pencils, your calculator, and spare batteries. No scratch paper, notes, or
books are allowed. Cell phones are not allowed anywhere close to the exam
room and are prohibited even during the short break between multiple-choice
and free-response sections. Better yet, LEAVE
YOUR CELL PHONE IN YOUR CAR.
|
|
|
Th
5/9/13
|
No additional HW due.
Class will begin with a “relaxed start” at 8:20. You will not be counted late
if you arrive in your seat by 8:25, but please try to arrive by 8:20 so that
we can get the class started with a minimum of shuffling and fuss. Karl and
Jared are permitted to arrive at 8:30, for reasons that will become clear.
|
|
|
F 5/9/13
|
Relaxed start at 8:20 to
8:25. Form VI students that still have cuts remaining may request cuts by
sending a request by 8:25. Remember, there is a free period during assembly
today.
|
|
|
M 5/13/13
|
Relaxed start at 8:15 today. We will also vote on
the starting times for the remainder of the week.
HW due: Estimate the following probabilities. Enter your guesses in writing,
and record them on a standard HW sheet. It is not expected that you have the
capability to answer all of these questions accurately. An estimate is
acceptable. Heein is permitted to use the same HW sheet for both HappyCal and STAtistics.
1. Player A rolls 2 fair dice. Player B rolls 4 fair dice. The probability of
interest is the probability that the maximum die roll for A is strictly
greater than the maximum die roll for B. For example, if A rolls (2, 5) and B
rolls (3, 4, 3, 2), then max(A) = 5 > Max(B) = 4,
and player A wins. However, if A rolls (5, 2) and B rolls (5, 1, 1, 4), then max(A) = 5, max(B) = 5, and B wins. We want to know the
probability that player A wins.
2. A random stream of 15,000 decimal digits is spewed out by a digital device
whose job it is to spew out random digits. The digits follow an approximately
uniform distribution, but of course there is no guarantee that the number of
0’s, 1’s, 2’s, etc. are exactly 1500 each. The probability of interest is the
probability that the sequence 2, 0, 1, 3 appears exactly twice when the
digits are viewed in order. The two occurrences of 2 0 1 3 may have any
number of intervening digits (0 or more) between them, but each occurrence of
2 0 1 3 must have those digits as consecutive digits.
3. Ten quadrillion (i.e., 1016) random capital letters, A through
Z, are generated. What is the probability that the word SHAKESPEARE appears
at least once in that immense list when the letters are viewed in order?
4. Two cards are drawn without replacement from a standard, well-shuffled
52-card deck. Given that at least one of the cards is an ace, what is the
probability that you have a pair of aces?
5. Two cards are drawn without replacement from a standard, well-shuffled
52-card deck. Given that the first card is an ace, what is the probability
that you have a pair of aces?
|
|
|
T 5/14/13
|
Relaxed start at 8:15 today. We didn’t have a quorum
yesterday, so we will vote today on the starting times for the remainder of
the week.
HW due:
Note: For all questions, both
yesterday and today, an estimate within 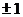 percentage point of
the true value is desired. For example, if the true answer is 0.941, you
would not be considered correct if you said “1,” even though that’s not a
terrible guess. After all, in real life, there’s a large difference between
something that is true 94.1% of the time (think of correct order execution at
your favorite fast-food restaurant) and something that is true 99.999% of the
time (correct air-traffic control for an arriving flight).
1. Estimate the probability of drawing a jack as the next card from a
well-shuffled deck, given that the leftmost card of the 2 cards you already
hold is an ace. The rightmost card of the 2 you already hold is not visible
to you.
2. Estimate the probability of drawing a jack as the next card from a
well-shuffled deck, given that at least one of the 2 cards you already hold
is an ace. (You do not look at either of the cards you are already holding.
Assume that you have already asked a trusted friend, “Is at least one of
these cards an ace?” and that she said yes.)
3. Explain how knowledge of the calculus helps in answering yesterday’s
question #3. Hint: If it didn’t
help you, then you weren’t doing it correctly.
4, 5. What two important metaknowledge life lessons have you learned as a result
of yesterday’s and today’s HW? If you learned a
third lesson (or more), feel free to write more.
|
|