|
M 4/1/13
|
Classes resume.
|
|
|
T 4/2/13
|
HW due: Read §12-4; write
§12-4 #3, 5, 6, and the following additional problem.
Additional problem:
Recall that a set I of real numbers
is defined to be open iff for any point x
of the set, there exists a neighborhood of x that is a subset of I.
Recall that a set J of real numbers
is defined to be closed iff every convergent sequence {an} formed from elements of J converges to an element of J.
In other words, J must contain all
of its limit points.
Note that open and closed are not complementary. A set
can be open but not closed, closed but not open,
both open and closed, or neither open nor closed.
Let Q denote the set of rational
numbers, i.e., numbers of the form 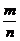 where m and n are integers and n where m and n are integers and n 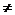 0. 0.
Explain
(a) why Q is not
open. (We did this in class. The purpose of this question is merely to
determine if you were paying attention.
(b) whether Q is closed or not. (Some people said Q was closed; others said Q
was not closed. Take a stand, and explain your reasoning.)
|
|
|
W 4/3/13
|
HW due:
1. Complete the HW that was assigned for yesterday. We will go over all
problems in class.
2. Read §§12-5 and 12-6.
3. Memorize at least one of the series in the second green box on p. 616.
(Ultimately, you will be required to memorize all 8.)
4. Try to prove, rigorously, that lim tn =
0 is a necessary condition for convergence of the sequence {tn}.
We will also do this proof in class today. At a minimum, a good start is
expected. (None of the previous efforts submitted by students exhibited a
thorough, rigorous, correct approach to this proof.)
|
|
|
Th
4/4/13
|
HW due:
1. Memorize at least one more series in the second green box on p. 616. That means
that you should now know 2 of them by heart.
2. Memorize the intervals of convergence for all 8 series on p. 616. You may
lightly write these in the margin of your textbook if you wish. The intervals
are the entire real line for the first five (exp, sine, cosine, sinh, and cosh), the half-open
interval (0, 2] for the natural log, (–1, 1) for the geometric series 1/(1 – x), and
[–1, 1] for the arctangent series.
3. Given that the interval of convergence of the natural log series is (0,
2], determine whether the interval is
(a) open (yes or no)
(b) closed (yes or no).
Give specific reasons for your answers to parts (a) and (b).
4. Finish your previously assigned HW problems.
5. There may also be a classroom note check for the proof that lim tn = 0 is a necessary condition for convergence
of an infinite series. Make sure that your proof is legible and complete,
since your notes substitute for the HW that was collected previously. Hint: If your notes are illegible or
incomplete, recopying them is a great way to reinforce and learn the
concepts.
|
|
|
F 4/5/13
|
HW due:
1. Memorize at least 2 more series in the second green box on p. 616. That
means that you are now responsible for 4 of them. All 8 intervals of
convergence (and associated radii of convergence, naturally) are also
required.
2. Write §12-5 #9-30 mo3.
3. In the instructions for Problems 1-6 on p. 627, insert the word “OPEN”
before the word “interval” in part b.
3. Write §12-6 #2-6 even.
|
|
|
M 4/8/13
|
HW due:
1. Memorize at least 2 more series in the second green box on p. 616. That
means that you are now responsible for 6 of them. All 8 intervals of
convergence (and associated radii of convergence, naturally) are also
required.
2. Read the green boxes at the top and middle of p. 630. The root test is not
an AP topic, but it is a good thing to know about.
3. Read §12-7. Reading notes are required, as always.
4. Read the green box on p. 640 and learn this test.
5. Write §12-7 #18.
6. Memorize the 3 green boxes on pp. 634 and 635. An open-notes quiz on this
material is possible.
7. Put a star next to the nth term
test on p. 635 to remind yourself that this is a test for divergence only. If lim tn = 0, that tells you nothing about whether
the series converges or not.
8. Read about the limit comparison
test, a super-useful test that can save you a lot of time.
|
|
|
T 4/9/13
|
HW due:
1. Be prepared for a quiz on all 8 series on p. 616, including intervals and
radii of convergence. Today you are responsible for both the “terms added up
format” and the “sigma notation format.”
2. Read §12-8. This is the final reading assignment for the year!
3. Write §12-7 #6-16 even.
|
|
|
W 4/10/13
|
HW due:
1. Reread §12-8. Make a second set of reading notes. This is difficult
material that will require several days to be thoroughly understood.
2. Write §12-7 #22, 25-30 all. Note:
For the convergent series in #25-30, state the exact value to which the series
converges.
|
|
|
Th
4/11/13
|
HW due:
1. Write §12-8 #3, 4, 23.
2. Since #3, 4, and 23 should not take you a full 35 minutes, use your
remaining time to improve recent problems, especially §12-7 #6-16 even and
#25-30 all.
|
|
|
F 4/12/13
|
HW due:
1. Prove the following identities, where z
is any complex number and i is the imaginary unit. You may use the supplemental
information presented in class lectures.
(a) cosh z = cos iz
(b) sinh iz = i sin z
2.(a) Write 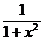 in the format in the format 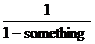 . .
This is supposed to be really, really
easy. Ask a friend for help if you aren’t seeing it.
(b) Use the geometric series expansion of the expression 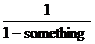 to rewrite to rewrite 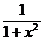 as a power series. as a power series.
(c) Find the interval of convergence for the series you
wrote in part (b). Justify your reasoning.
(d) Use a power series approach to find 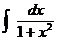 . .
(e) On what domain is your result in part (d) valid?
Explain briefly.
3. How many terms of the Taylor series for ln x are needed to compute ln 1.8 within an accuracy of 0.000001? Provide your
answer both
(a) by using the Lagrange error bound, and
(b) by using the AST error bound, if applicable. (In other
words, justify your steps if the AST bound applies.)
4. Compute 1.84.6 as if you were a computer program running inside
your calculator. The only permitted operations are addition, subtraction,
multiplication, and division. No root-taking, exponentiation, or
transcendental function evaluations are permitted. Describe how to do this!
Previously solved problems in today’s assignment may be incorporated by
reference if you find them to be helpful.
|
|
|
M 4/15/13
|
HW due: Work on AP review
problems. By now, you should have a review book. Keep a written log of all your
responses (if free-response) or scratch work (if multiple choice). List the
page number and problem number for each question. Keep a time log. A minimum
of 35 minutes is required. More is
better. However, steady daily work for a modest period of time is more
helpful than sporadic “cram” sessions.
If you do not have a review book yet (or even if you do), you can also find
excellent free-response review problems and scoring guidelines here.
|
|
|
T 4/16/13
|
HW due: Same as yesterday,
with the addition that you should log both days’ work on your AP
review log sheet. If you do not have Excel, you can request a copy today
during class, and one will be provided for you so that you can fill it in.
|
|
|
W 4/17/13
|
HW due: Continue working on
your AP
review log sheet, plus the following problems. The second is much easier
than the first.
1. How many terms of the Maclaurin series for cosh x are
needed in order to ensure accuracy within 0.001 for any x-value in the interval [–2, 2]? Note: It is not considered “sporting” to use the value of e (approximately 2.718281828459) when
computing error bounds, since if you knew e,
you could of course calculate cosh x directly from the definition.
Therefore, use 3 as an upper bound for e
when using exponentials with positive exponents, and when raising e to a negative power, use 2 or 2.5 as
a value for e in order to create a
conservative upper bound.
2. How many terms of the Maclaurin series for sin x are needed in order to ensure
accuracy within 0.00000001 for any x-value
in the interval 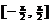 ? ?
In class: Review, review, review. If you want to ask about Euler’s Method,
you may.
|
|
|
Th
4/18/13
|
Test (100 pts.) on everything (all topics for
the entire year). Emphasis will be on power series in Chapter 12.
Calculator will be permitted on all portions.
Format will be approximately as follows:
30 points on 1 free-response question (AP style with curve)
30 points on 5 multiple-choice questions (AP style with curve)
15 points on finding the errors in a proof you have never seen before
25 points on approximately 5 randomly chosen questions from various parts of
the year (no curve)
|
|
|
F 4/19/13
|
HW due: Rewrite the
AP free-response question and questions
10 and 11 from yesterday’s test. Note that the AP question is called #3
in the online source but was #6 on the test you took. Perfection is expected.
You may use online resources, friends, or any other resource you wish, with
one exception: NO OUTRIGHT COPYING IS PERMITTED. In other words, when
you write up the final version of the solution to each problem, you need to
do it from your own brain to your own pencil.
On your AP review sheet, you may list these as “4/18 Test #6,” “4/18 Test
#10,” and “4/18 Test #11.” If they take you the full 35 minutes to do, you
need not log any additional problems for today.
|
|
|
M 4/22/13
|
No school (Phi Beta Kappa Day).
However, continue logging daily work on your AP review logsheet.
You may take one day of rest per week.
|
|
|
T 4/23/13
|
HW due: Continue logging
daily work on your AP review logsheet.
|
|
|
W 4/24/13
|
HW due:
1. Correct the problem that we did incorrectly at the end of class yesterday.
Your fearless teacher wrote the diff. eq. on the board as 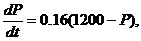 which is correct, but
then worked with it as if it had been given as which is correct, but
then worked with it as if it had been given as
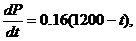 which is not
correct. Don’t repeat your teacher’s mistake! which is not
correct. Don’t repeat your teacher’s mistake!
Here is the problem:
The number of people who have heard a rumor after time t, where t is measured
in days, is P(t). The rate at which the rumor’s reach is growing is given by 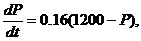 and at time 0, there
are 200 people who have heard the rumor. Find the number of people who have
heard the rumor at the end of 2 days. and at time 0, there
are 200 people who have heard the rumor. Find the number of people who have
heard the rumor at the end of 2 days.
2. Do more AP review. Log all problems on your AP review logsheet,
and keep all written work in your HW binder. Your written work should include
the page number and problem number for each problem. For multiple-choice
problems, show your answer, the correct answer, and anything you learned from
the question, along with your scratch work (if any). For free-response
problems, show your entire writeup, written out as
if you were taking the AP exam. Your writeup must
be legible and coherent. No random chicken-scratching!
|
|
|
Th
4/25/13
|
HW due: Continue working on
your AP review logsheet.
|
|
|
F 4/26/13
|
HW due: Continue working on
your AP review logsheet.
In class: 2007 #6 with scoring rubric.
|
|
|
M 4/29/13
|
HW due: Continue working on
your AP review logsheet.
In class: Giant review for the giant quizzes.
Because most students have test conflicts on at least one of the 3 days, you are
not required to take all 3 giant quizzes. Check-in and homework scan at 8:35
will be permitted on one day of your choice (Tuesday, Wednesday, or
Thursday). If you are sick Tuesday, then obviously you need to come on both
Wednesday and Thursday. If you are a glutton for punishment and take all 3
quizzes, the best 2 will be counted. All scoring will be on an AP-style
curve.
|
|
|
T 4/30/13
|
Giant Quiz I (50 points).
Format will be 9 MC without calculator, 1 FR with calculator, total of 33
minutes (49.5 for extended time).
|
|